subchain
Extract Markov subchain
Syntax
Description
Examples
Input Arguments
Output Arguments
Algorithms
State
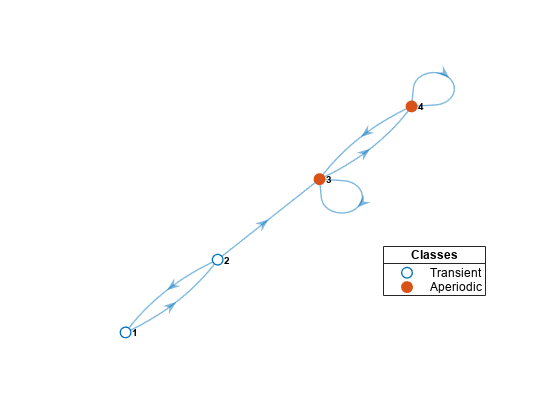
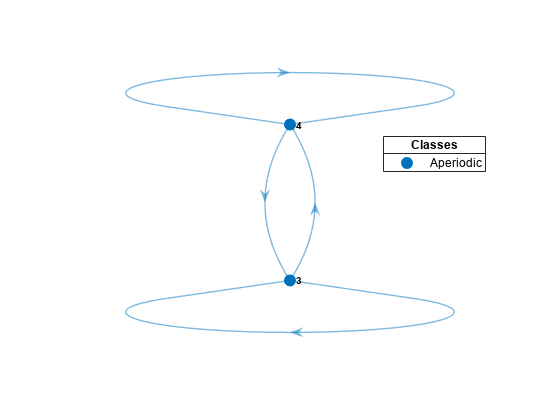
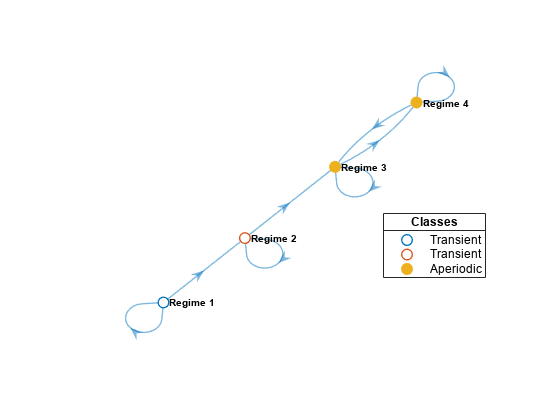
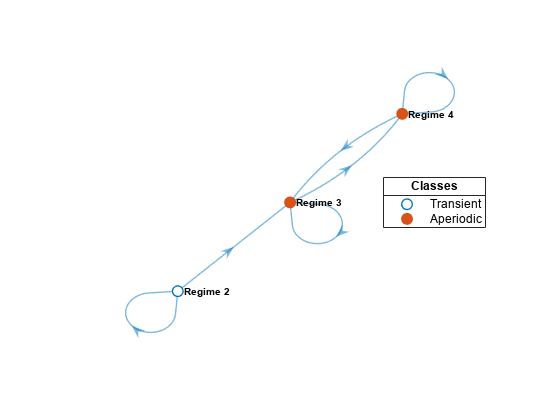
jis reachable from stateiif there is a nonzero probability of moving fromitojin a finite number of steps.subchaindetermines reachability by forming the transitive closure of the associated digraph, then enumerating one-step transitions.Subchains are closed under reachability to ensure that the transition matrix of
scremains stochastic (that is, rows sum to1), with transition probabilities identical to the transition probabilities inmc.P.If you specify a state in a recurrent communicating class, then
subchainextracts the entire communicating class. If you specify a state in a transient communicating class, thensubchainextracts the transient class and all classes reachable from the transient class. To extract a unichain, specify a state in each component transient class. Seeclassify.
References
[1] Gallager, R.G. Stochastic Processes: Theory for Applications. Cambridge, UK: Cambridge University Press, 2013.
[2] Horn, R., and C. R. Johnson. Matrix Analysis. Cambridge, UK: Cambridge University Press, 1985.
Version History
Introduced in R2017b