mixsemiconjugateblm
Bayesian linear regression model with semiconjugate priors for stochastic search variable selection (SSVS)
Description
The Bayesian linear regression model object mixsemiconjugateblm
specifies the joint prior distribution of the regression coefficients and the disturbance
variance (β, σ2) for
implementing SSVS (see [1] and [2]) assuming β and
σ2 are dependent random
variables.
In general, when you create a Bayesian linear regression model object, it specifies the joint prior distribution and characteristics of the linear regression model only. That is, the model object is a template intended for further use. Specifically, to incorporate data into the model for posterior distribution analysis and feature selection, pass the model object and data to the appropriate object function.
Creation
Syntax
Description
PriorMdl = mixsemiconjugateblm(NumPredictors)PriorMdl) composed of
NumPredictors predictors and an intercept, and sets the
NumPredictors property. The joint prior distribution of
(β, σ2) is
appropriate for implementing SSVS for predictor selection [2]. PriorMdl
is a template that defines the prior distributions and the dimensionality of
β.
PriorMdl = mixsemiconjugateblm(NumPredictors,Name,Value)NumPredictors) using name-value pair arguments. Enclose each
property name in quotes. For example,
mixsemiconjugateblm(3,'Probability',abs(rand(4,1))) specifies
random prior regime probabilities for all four coefficients in the model.
Properties
You can set writable property values when you create the model object by using name-value argument syntax, or after you create the model object by using dot notation. For example, to exclude an intercept from the model, enter
PriorMdl.Intercept = false;
Number of predictor variables in the Bayesian multiple linear regression model, specified as a nonnegative integer.
NumPredictors must be the same as the number of columns in your predictor data, which you specify during model estimation or simulation.
When specifying NumPredictors, exclude any intercept term for the value.
After creating a model, if you change the of value NumPredictors using dot
notation, then these parameters revert to the default values:
Variable names (
VarNames)Prior mean of β (
Mu)Prior variances of β for each regime (
V)Prior correlation matrix of β (
Correlation)Prior regime probabilities (
Probability)
Data Types: double
Flag for including a regression model intercept, specified as a value in this table.
| Value | Description |
|---|---|
false | Exclude an intercept from the regression model. Therefore, β is a p-dimensional vector, where p is the value of NumPredictors. |
true | Include an intercept in the regression model. Therefore, β is a (p + 1)-dimensional vector. This specification causes a T-by-1 vector of ones to be prepended to the predictor data during estimation and simulation. |
If you include a column of ones in the predictor data for an intercept
term, then set Intercept to false.
Example: 'Intercept',false
Data Types: logical
Predictor variable names for displays, specified as a string vector or cell vector of
character vectors. VarNames must contain
NumPredictors elements.
VarNames( is the name of the
variable in column j)j of the predictor data set, which you
specify during estimation, simulation, or forecasting.
The default is {'Beta(1)','Beta(2),...,Beta(,
where p)}p is the value of NumPredictors.
Example: 'VarNames',["UnemploymentRate"; "CPI"]
Data Types: string | cell | char
Component-wise mean hyperparameter of the Gaussian mixture prior on
β, specified as an (Intercept + NumPredictors)-by-2 numeric
matrix. The first column contains the prior means for component 1 (the variable-inclusion
regime, that is, γ = 1). The second column contains the prior means for
component 2 (the variable-exclusion regime, that is, γ = 0).
If
Interceptisfalse, thenMuhasNumPredictorsrows.mixsemiconjugateblmsets the prior mean of theNumPredictorscoefficients corresponding to the columns in the predictor data set, which you specify during estimation, simulation, or forecasting.Otherwise,
MuhasNumPredictors + 1elements. The first element corresponds to the prior means of the intercept, and all other elements correspond to the predictor variables.
Tip
To perform SSVS, use the default value of Mu.
Example: In a 3-coefficient model, 'Mu',[0.5 0; 0.5 0; 0.5 0] sets
the component 1 prior mean of all coefficients to 0.5 and sets the
component 2 prior mean of all coefficients to 0.
Data Types: double
Component-wise variance hyperparameter of the Gaussian mixture prior on
β, an (Intercept + NumPredictors)-by-2 positive
numeric matrix. The first column contains the prior variance factors for component 1 (the
variable-inclusion regime, that is, γ = 1). The second column contains the
prior variance factors for component 2 (the variable-exclusion regime, that is,
γ = 0).
If
Interceptisfalse, thenVhasNumPredictorsrows.mixsemiconjugateblmsets the prior variance factor of theNumPredictorscoefficients corresponding to the columns in the predictor data set, which you specify during estimation, simulation, or forecasting.Otherwise,
VhasNumPredictors + 1elements. The first element corresponds to the prior variance factor of the intercept, and all other elements correspond to the predictor variables.
Tip
To perform SSVS, specify a larger variance factor for regime 1 than for regime 2 (for all
j, specifyV(>j,1)V().j,2)For more details on what value to specify for
V, see [1].
Example: In a 3-coefficient model, 'V',[100 1; 100 1; 100 1] sets
the component 1 prior variance factor of all coefficients to 100 and
sets the component 2 prior variance factor of all coefficients to
1.
Data Types: double
Prior probability distribution for the variable inclusion and exclusion regimes,
specified as an (Intercept +
NumPredictors)-by-1 numeric vector of values in [0,1], or a function
handle in the form @fcnName, where fcnName is the function
name. Probability represents the prior probability distribution of
γ =
{γ1,…,γK},
where:
K =
Intercept+NumPredictors, which is the number of coefficients in the regression model.γk ∈ {0,1} for k = 1,…,K. Therefore, the sample space has a cardinality of 2K.
γk = 1 indicates variable
VarNames(is included in the model, and γk = 0 indicates that the variable is excluded from the model.k)
If Probability is a numeric vector:
Rows correspond to the variable names in
VarNames. For models containing an intercept, the prior probability for intercept inclusion isProbability(1).For
kkProbability(k).Prior probabilities of the variable-inclusion regime, among all variables and the intercept, are independent.
If Probability is a function handle, then it represents a custom prior distribution of the variable-inclusion regime probabilities. The corresponding function must have this declaration statement (the argument and function names can vary):
logprob = regimeprior(varinc)
logprobis a numeric scalar representing the log of the prior distribution. You can write the prior distribution up to a proportionality constant.varincis a K-by-1 logical vector. Elements correspond to the variable names inVarNamesand indicate the regime in which the corresponding variable exists.varinc(=k)trueindicatesVarName(is included in the model, andk)varinc(=k)falseindicates it is excluded from the model.
You can include more input arguments, but they must be known when you call
mixsemiconjugateblm.
For details on what value to specify for Probability, see [1].
Example: In a 3-coefficient model, 'Probability',rand(3,1) assigns
random prior variable-inclusion probabilities to each coefficient.
Data Types: double | function_handle
Prior correlation matrix of β for both components in the mixture
model, specified as an (Intercept +
NumPredictors)-by-(Intercept +
NumPredictors) numeric, positive definite matrix. Consequently, the
prior covariance matrix for component jdiag(sqrt(V(:,,
where j)))*Correlation*diag(sqrt(V(:,j)))V is the matrix of coefficient variances.
Rows and columns correspond to the variable names in VarNames.
By default, regression coefficients are uncorrelated, conditional on the regime.
Note
You can supply any appropriately sized numeric matrix. However, if your specification is not
positive definite, mixsemiconjugateblm issues a warning and replaces your
specification with CorrelationPD,
where:
CorrelationPD = 0.5*(Correlation + Correlation.');
Tip
For details on what value to specify for Correlation, see [1].
Data Types: double
Shape hyperparameter of the inverse gamma prior on σ2, specified as a numeric scalar.
A must be at least –(Intercept +
NumPredictors)/2.
With B held fixed, the inverse gamma distribution becomes taller and more
concentrated as A increases. This characteristic weighs the prior model
of σ2 more heavily than the likelihood during
posterior estimation.
For the functional form of the inverse gamma distribution, see Analytically Tractable Posteriors.
Example: 'A',0.1
Data Types: double
Scale parameter of inverse gamma prior on σ2,
specified as a positive scalar or Inf.
With A held fixed, the inverse gamma distribution becomes taller and more
concentrated as B increases. This characteristic weighs the prior model
of σ2 more heavily than the likelihood during
posterior estimation.
Example: 'B',5
Data Types: double
Object Functions
estimate | Perform predictor variable selection for Bayesian linear regression models |
simulate | Simulate regression coefficients and disturbance variance of Bayesian linear regression model |
forecast | Forecast responses of Bayesian linear regression model |
plot | Visualize prior and posterior densities of Bayesian linear regression model parameters |
summarize | Distribution summary statistics of Bayesian linear regression model for predictor variable selection |
Examples
Consider the multiple linear regression model that predicts the US real gross national product (GNPR) using a linear combination of industrial production index (IPI), total employment (E), and real wages (WR).
For all , is a series of independent Gaussian disturbances with a mean of 0 and variance .
Assume these prior distributions for = 0,...,3:
, where and are independent, standard normal random variables. Therefore, the coefficients have a Gaussian mixture distribution. Assume all coefficients are conditionally independent, a priori.
. and are the shape and scale, respectively, of an inverse gamma distribution.
and it represents the random variable-inclusion regime variable with a discrete uniform distribution.
Create a prior model for SSVS. Specify the number of predictors p.
p = 3; PriorMdl = mixsemiconjugateblm(p);
PriorMdl is a mixsemiconjugateblm Bayesian linear regression model object representing the prior distribution of the regression coefficients and disturbance variance. mixsemiconjugateblm displays a summary of the prior distributions at the command line.
Alternatively, you can create a prior model for SSVS by passing the number of predictors to bayeslm and setting the ModelType name-value pair argument to 'mixsemiconjugate'.
MdlBayesLM = bayeslm(p,'ModelType','mixsemiconjugate')
MdlBayesLM =
mixsemiconjugateblm with properties:
NumPredictors: 3
Intercept: 1
VarNames: {4×1 cell}
Mu: [4×2 double]
V: [4×2 double]
Probability: [4×1 double]
Correlation: [4×4 double]
A: 3
B: 1
| Mean Std CI95 Positive Distribution
------------------------------------------------------------------------------
Intercept | 0 2.2472 [-5.201, 5.201] 0.500 Mixture distribution
Beta(1) | 0 2.2472 [-5.201, 5.201] 0.500 Mixture distribution
Beta(2) | 0 2.2472 [-5.201, 5.201] 0.500 Mixture distribution
Beta(3) | 0 2.2472 [-5.201, 5.201] 0.500 Mixture distribution
Sigma2 | 0.5000 0.5000 [ 0.138, 1.616] 1.000 IG(3.00, 1)
Mdl and MdlBayesLM are equivalent model objects.
You can set writable property values of created models using dot notation. Set the regression coefficient names to the corresponding variable names.
PriorMdl.VarNames = ["IPI" "E" "WR"]
PriorMdl =
mixsemiconjugateblm with properties:
NumPredictors: 3
Intercept: 1
VarNames: {4×1 cell}
Mu: [4×2 double]
V: [4×2 double]
Probability: [4×1 double]
Correlation: [4×4 double]
A: 3
B: 1
| Mean Std CI95 Positive Distribution
------------------------------------------------------------------------------
Intercept | 0 2.2472 [-5.201, 5.201] 0.500 Mixture distribution
IPI | 0 2.2472 [-5.201, 5.201] 0.500 Mixture distribution
E | 0 2.2472 [-5.201, 5.201] 0.500 Mixture distribution
WR | 0 2.2472 [-5.201, 5.201] 0.500 Mixture distribution
Sigma2 | 0.5000 0.5000 [ 0.138, 1.616] 1.000 IG(3.00, 1)
MATLAB® associates the variable names to the regression coefficients in displays.
Plot the prior distributions.
plot(PriorMdl);
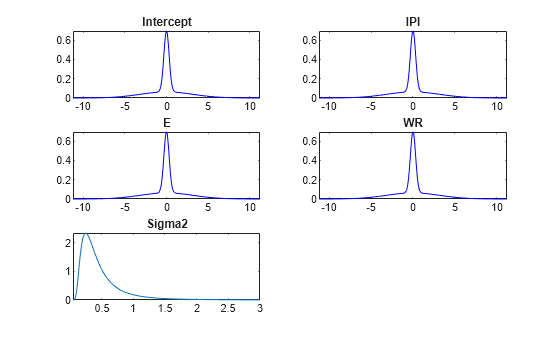
The prior distribution of each coefficient is a mixture of two Gaussians: both components have a mean of zero, but component 1 has a large variance relative to component 2. Therefore, their distributions are centered at zero and have the spike-and-slab appearance.
Consider the linear regression model in Create Prior Model for SSVS.
Create a prior model for performing SSVS. Assume that and are independent (a semiconjugate mixture model). Specify the number of predictors p and the names of the regression coefficients.
p = 3; PriorMdl = mixsemiconjugateblm(p,'VarNames',["IPI" "E" "WR"]);
Display the prior regime probabilities and Gaussian mixture variance factors of the prior .
priorProbabilities = table(PriorMdl.Probability,'RowNames',PriorMdl.VarNames,... 'VariableNames',"Probability")
priorProbabilities=4×1 table
Probability
___________
Intercept 0.5
IPI 0.5
E 0.5
WR 0.5
priorV = array2table(PriorMdl.V,'RowNames',PriorMdl.VarNames,... 'VariableNames',["gammaIs1" "gammaIs0"])
priorV=4×2 table
gammaIs1 gammaIs0
________ ________
Intercept 10 0.1
IPI 10 0.1
E 10 0.1
WR 10 0.1
PriorMdl stores prior regime probabilities in the Probability property and the regime variance factors in the V property. The default prior probability of variable inclusion is 0.5. The default variance factors for each coefficient are 10 for the variable-inclusion regime and 0.01 for the variable-exclusion regime.
Load the Nelson-Plosser data set. Create variables for the response and predictor series.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,'GNPR'};
Implement SSVS by estimating the marginal posterior distributions of and . Because SSVS uses Markov chain Monte Carlo (MCMC) for estimation, set a random number seed to reproduce the results.
rng(1); PosteriorMdl = estimate(PriorMdl,X,y);
Method: MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution Regime
-------------------------------------------------------------------------------
Intercept | -1.5629 2.6816 [-7.879, 2.703] 0.300 Empirical 0.5901
IPI | 4.6217 0.1222 [ 4.384, 4.865] 1.000 Empirical 1
E | 0.0004 0.0002 [ 0.000, 0.001] 0.976 Empirical 0.0918
WR | 2.6098 0.3691 [ 1.889, 3.347] 1.000 Empirical 1
Sigma2 | 50.9169 9.4955 [35.838, 72.707] 1.000 Empirical NaN
PosteriorMdl is an empiricalblm model object that stores draws from the posterior distributions of and given the data. estimate displays a summary of the marginal posterior distributions at the command line. Rows of the summary correspond to regression coefficients and the disturbance variance, and columns correspond to characteristics of the posterior distribution. The characteristics include:
CI95, which contains the 95% Bayesian equitailed credible intervals for the parameters. For example, the posterior probability that the regression coefficient ofEis in[0.000, 0.001]is 0.95.Regime, which contains the marginal posterior probability of variable inclusion ( for a variable). For example, the posterior probability thatEshould be included in the model is 0.0918.
Assuming that variables with Regime < 0.1 should be removed from the model, the results suggest that you can exclude the unemployment rate from the model.
By default, estimate draws and discards a burn-in sample of size 5000. However, a good practice is to inspect a trace plot of the draws for adequate mixing and lack of transience. Plot a trace plot of the draws for each parameter. You can access the draws that compose the distribution (the properties BetaDraws and Sigma2Draws) using dot notation.
figure; for j = 1:(p + 1) subplot(2,2,j); plot(PosteriorMdl.BetaDraws(j,:)); title(sprintf('%s',PosteriorMdl.VarNames{j})); end
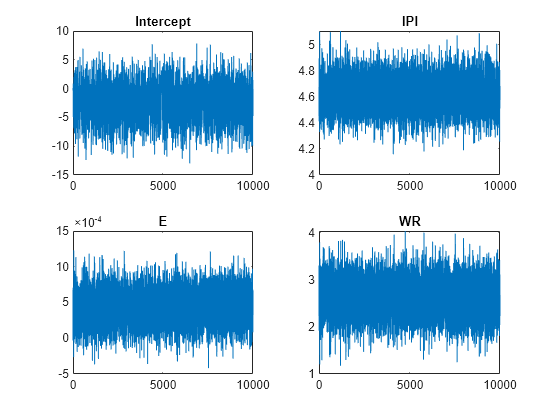
figure;
plot(PosteriorMdl.Sigma2Draws);
title('Sigma2');
The trace plots indicate that the draws seem to mix well. The plots show no detectable transience or serial correlation, and the draws do not jump between states.
Consider the linear regression model in Create Prior Model for SSVS.
Load the Nelson-Plosser data set. Create variables for the response and predictor series.
load Data_NelsonPlosser VarNames = ["IPI" "E" "WR"]; X = DataTable{:,VarNames}; y = DataTable{:,"GNPR"};
Assume the following:
The intercept is in the model with probability 0.9.
IPIandEare in the model with probability 0.75.If
Eis included in the model, then the probability thatWRis included in the model is 0.9.If
Eis excluded from the model, then the probability thatWRis included is 0.25.
Declare a function named priorssvsexample.m that:
Accepts a logical vector indicating whether the intercept and variables are in the model (
truefor model inclusion). Element 1 corresponds to the intercept, and the rest of the elements correspond to the variables in the data.Returns a numeric scalar representing the log of the described prior regime probability distribution.
function logprior = priorssvsexample(varinc) %PRIORSSVSEXAMPLE Log prior regime probability distribution for SSVS % PRIORSSVSEXAMPLE is an example of a custom log prior regime probability % distribution for SSVS with dependent random variables. varinc is % a 4-by-1 logical vector indicating whether 4 coefficients are in a model % and logPrior is a numeric scalar representing the log of the prior % distribution of the regime probabilities. % % Coefficients enter a model according to these rules: % * varinc(1) is included with probability 0.9. % * varinc(2) and varinc(3) are in the model with probability 0.75. % * If varinc(3) is included in the model, then the probability that % varinc(4) is included in the model is 0.9. % * If varinc(3) is excluded from the model, then the probability % that varinc(4) is included is 0.25. logprior = log(0.9) + 2*log(0.75) + log(varinc(3)*0.9 + (1-varinc(3))*0.25); end
Create a prior model for performing SSVS. Assume that  and
and  are independent (a semiconjugate mixture model). Specify the number of predictors
are independent (a semiconjugate mixture model). Specify the number of predictors p the names of the regression coefficients, and custom, prior probability distribution of the variable-inclusion regimes.
p = 3; PriorMdl = mixsemiconjugateblm(p,'VarNames',["IPI" "E" "WR"],... 'Probability',@priorssvsexample);
Implement SSVS by estimating the marginal posterior distributions of  and
and  . Because SSVS uses MCMC for estimation, set a random number seed to reproduce the results.
. Because SSVS uses MCMC for estimation, set a random number seed to reproduce the results.
rng(1); PosteriorMdl = estimate(PriorMdl,X,y);
Method: MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution Regime
-------------------------------------------------------------------------------
Intercept | -1.4658 2.6046 [-7.781, 2.546] 0.308 Empirical 0.5516
IPI | 4.6227 0.1222 [ 4.385, 4.866] 1.000 Empirical 1
E | 0.0004 0.0002 [ 0.000, 0.001] 0.976 Empirical 0.2557
WR | 2.6105 0.3692 [ 1.886, 3.346] 1.000 Empirical 1
Sigma2 | 50.9621 9.4999 [35.860, 72.596] 1.000 Empirical NaN
Assuming, that variables with Regime < 0.1 should be removed from the model, the results suggest that you can include all variables in the model.
Consider the regression model in Create Prior Model for SSVS.
Perform SSVS:
Create a Bayesian regression model for SSVS with a semiconjugate prior for the data likelihood. Use the default settings.
Hold out the last 10 periods of data from estimation.
Estimate the marginal posterior distributions.
p = 3; PriorMdl = bayeslm(p,'ModelType','mixsemiconjugate','VarNames',["IPI" "E" "WR"]); load Data_NelsonPlosser fhs = 10; % Forecast horizon size X = DataTable{1:(end - fhs),PriorMdl.VarNames(2:end)}; y = DataTable{1:(end - fhs),'GNPR'}; XF = DataTable{(end - fhs + 1):end,PriorMdl.VarNames(2:end)}; % Future predictor data yFT = DataTable{(end - fhs + 1):end,'GNPR'}; % True future responses rng(1); % For reproducibility PosteriorMdl = estimate(PriorMdl,X,y,'Display',false);
Forecast responses using the posterior predictive distribution and the future predictor data XF. Plot the true values of the response and the forecasted values.
yF = forecast(PosteriorMdl,XF); figure; plot(dates,DataTable.GNPR); hold on plot(dates((end - fhs + 1):end),yF) h = gca; hp = patch([dates(end - fhs + 1) dates(end) dates(end) dates(end - fhs + 1)],... h.YLim([1,1,2,2]),[0.8 0.8 0.8]); uistack(hp,'bottom'); legend('Forecast Horizon','True GNPR','Forecasted GNPR','Location','NW') title('Real Gross National Product: 1909 - 1970'); ylabel('rGNP'); xlabel('Year'); hold off
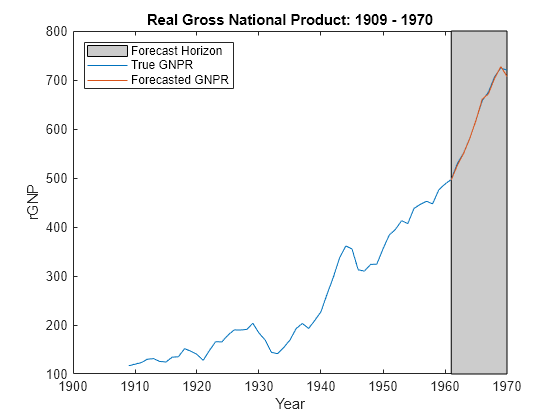
yF is a 10-by-1 vector of future values of real GNP corresponding to the future predictor data.
Estimate the forecast root mean squared error (RMSE).
frmse = sqrt(mean((yF - yFT).^2))
frmse = 4.5935
The forecast RMSE is a relative measure of forecast accuracy. Specifically, you estimate several models using different assumptions. The model with the lowest forecast RMSE is the best-performing model of the ones being compared.
When you perform Bayesian regression with SSVS, a best practice is to tune the hyperparameters. One way to do so is to estimate the forecast RMSE over a grid of hyperparameter values, and choose the value that minimizes the forecast RMSE.
Copyright 2018 The MathWorks, Inc.
More About
A Bayesian linear regression model treats the parameters β and σ2 in the multiple linear regression (MLR) model yt = xtβ + εt as random variables.
For times t = 1,...,T:
yt is the observed response.
xt is a 1-by-(p + 1) row vector of observed values of p predictors. To accommodate a model intercept, x1t = 1 for all t.
β is a (p + 1)-by-1 column vector of regression coefficients corresponding to the variables that compose the columns of xt.
εt is the random disturbance with a mean of zero and Cov(ε) = σ2IT×T, while ε is a T-by-1 vector containing all disturbances. These assumptions imply that the data likelihood is
ϕ(yt;xtβ,σ2) is the Gaussian probability density with mean xtβ and variance σ2 evaluated at yt;.
Before considering the data, you impose a joint prior distribution assumption on (β,σ2). In a Bayesian analysis, you update the distribution of the parameters by using information about the parameters obtained from the likelihood of the data. The result is the joint posterior distribution of (β,σ2) or the conditional posterior distributions of the parameters.
Stochastic search variable selection (SSVS) is a predictor variable selection method for Bayesian linear regression that searches the space of potential models for models with high posterior probability, and averages the models it finds after it completes the search.
SSVS assumes that the prior distribution of each regression coefficient is a mixture of two Gaussian distributions, and the prior distribution of σ2 is inverse gamma with shape A and scale B. Let γ = {γ1,…,γK} be a latent, random regime indicator for the regression coefficients β, where:
K is the number of coefficients in the model (
Intercept+NumPredictors). γk = 1 means that βk|σ2,γk is Gaussian with mean 0 and variance c1.γk = 0 means that a predictor is Gaussian with mean 0 and variance c2.
A probability mass function governs the distribution of γ, and the sample space of γ is composed of 2K elements.
More specifically, given γk and σ2, βk = γkc1Z + (1 – γk)c2Z, where:
Z is a standard normal random variable.
For conjugate models (
mixconjugateblm), cj = σ2Vj, j = 1,2.For semiconjugate models (
mixsemiconjugateblm), cj = Vj.
c1 is relatively large, which implies that the corresponding predictor is more likely to be in the model. c2 is relatively small, which implies that the corresponding predictor is less likely to be in the model because distribution is dense around 0.
In this framework, if the potential exists for a total of K coefficients in a model, then the space has 2K models through which to search. Because computing posterior probabilities of all 2K models can be computationally expensive, SSVS uses MCMC to sample γ = {γ1,…,γK} and estimate posterior probabilities of corresponding models. The models that the algorithm chooses often have higher posterior probabilities. The algorithm composes the estimated posterior distributions of β and σ2 by computing the weighted average of the sampled models. The algorithm attributes a larger weight to those models sampled more often.
The resulting posterior distribution for semiconjugate mixture models is analytically intractable. For details on the posterior distribution, see Analytically Tractable Posteriors.
Alternative Functionality
The bayeslm function can create any supported prior model object for Bayesian linear regression.
References
[1] George, E. I., and R. E. McCulloch. "Variable Selection Via Gibbs Sampling." Journal of the American Statistical Association. Vol. 88, No. 423, 1993, pp. 881–889.
[2] Koop, G., D. J. Poirier, and J. L. Tobias. Bayesian Econometric Methods. New York, NY: Cambridge University Press, 2007.
Version History
Introduced in R2018b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)