estimate
Fit Markov-switching dynamic regression model to data
Syntax
Description
EstMdl = estimate(Mdl,Mdl0,Y)Mdl. estimate fits the model to the response
data Y, and initializes the estimation procedure by treating the
parameter values of the fully specified Markov-switching dynamic regression model
Mdl0 as initial values. estimate uses a
version of the expectation-maximization (EM) algorithm described by Hamilton [3].
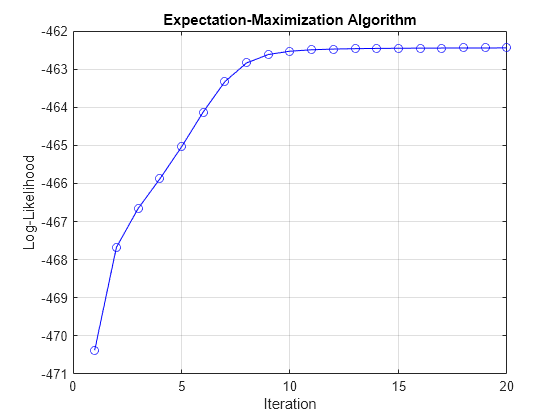
EstMdl = estimate(Mdl,Mdl0,Y,Name,Value)'IterationPlot',true displays a plot of the loglikelihood versus the iteration step, after the algorithm terminates.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Tips
In [4], Hamilton cautions: "Although a researcher might be tempted to use the most general specification possible, with all the parameters changing across a large number of regimes...in practice this is usually asking more than the data can deliver." Hamilton recommends model parsimony and selective estimation, to "limit the focus to a few of the most important parameters that are likely to change."
Data-generating processes with low variances can lead to difficulties in state inference and subsequent parameter estimation. In such cases, consider scaling the data. The variance scales quadratically.
Algorithms
estimateimplements a version of the EM algorithm described in [2], [3], and [4]. Given an initial estimate of model parametersMdl0,estimateiterates the following process until convergence:Expectation step —
estimateappliessmoothto the data to obtain inferences of latent state probabilities at each time step and an estimate of the overall data loglikelihood.Maximization step —
estimateuses the expected smoothed probabilities from the expectation step to weight the data before updating parameter estimates in each submodel.
Likelihood surfaces for the mixture densities of switching models can contain local maxima and singularities [2]. If so, the largest local maximum with a nonzero model variance is considered the maximum likelihood estimate (MLE). If
Mdl0is in the neighborhood of the MLE,estimatetypically converges to it, but this convergence is not guaranteed.estimatehandles two types of constraints:Constraints on submodel parameters, which the
estimateobject function of thevarmobject enforces at each maximization stepConstraints on transition probabilities, which
estimateenforces by projecting a maximal estimate of the transition matrix onto the constrained parameter space after each iteration
Constraints on submodel innovations variances and covariances are unsupported.
estimatecomputes innovations covariances after estimation, regardless of their values.
References
[2] Hamilton, J. D. "Analysis of Time Series Subject to Changes in Regime." Journal of Econometrics. Vol. 45, 1990, pp. 39–70.
[3] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[4] Hamilton, J. D. "Macroeconomic Regimes and Regime Shifts." In Handbook of Macroeconomics. (H. Uhlig and J. Taylor, eds.). Amsterdam: Elsevier, 2016.
[5] Kole, E. "Regime Switching Models: An Example for a Stock Market Index." Rotterdam, NL: Econometric Institute, Erasmus School of Economics, 2010.
Version History
Introduced in R2019b