filter
Filter disturbances through regression model with ARIMA errors
Description
Y = filter(Mdl,Z)Y resulting
from filtering the numeric array of one or more underlying disturbance series
Z through the fully specified, univariate regression model with
ARIMA errors Mdl. Z is associated with the error
model innovations process that drives the specified regression model with ARIMA
errors.
Tbl2 = filter(Mdl,Tbl1)Tbl2 containing the results from
filtering the paths of disturbances in the input table or timetable
Tbl1 through Mdl. The disturbance variable in
Tbl1 is associated with the model innovations process that drives
Mdl. (since R2023b)
filter selects the variable
Mdl.SeriesName, or the sole variable in Tbl1, as
the disturbance variable to filter through the model. To select a different variable in
Tbl1 to filter through the model, use the
DisturbanceVariable name-value argument.
[___] = filter(___,
specifies options using one or more name-value arguments in
addition to any of the input argument combinations in previous syntaxes.
Name,Value)filter returns the output argument combination for the
corresponding input arguments. For example, filter(Mdl,Z,X=Pred,Z0=PSZ) specifies the
predictor data Pred for the model regression component and the
observed errors in the presample period PSZ to initialize the
model.
Examples
Compute the impulse response function (IRF) of an innovation shock to the regression model with ARMA(2,1) errors. Supply the innovation shock as a vector.
The IRF assesses the dynamic behavior of a system to a one-time shock. Typically, the magnitude of the shock is 1. Alternatively, it might be more meaningful to examine an IRF of an innovation shock with a magnitude of one standard deviation.
In regression models with ARIMA errors,
The IRF is invariant to the behavior of the predictors and the intercept.
The IRF of the model is defined as the impulse response of the unconditional disturbances as governed by the ARIMA error component.
Create the following regression model with ARMA(2,1) errors:
where is Gaussian with variance 0.1.
Mdl = regARIMA(Intercept=0,AR={0.5 -0.8},MA=-0.5, ...
Variance=0.1);When you construct an impulse response function for a regression model with ARIMA errors, you must set Intercept to 0.
Simulate the first 30 responses of the impulse response function by generating an error series with a one-time impulse with magnitude equal to one standard deviation, and then filter it. Also, use impulse to compute the IRF.
z = [sqrt(Mdl.Variance); zeros(29,1)]; % Shock of 1 std
yFltr = filter(Mdl,z);
yImpls = impulse(Mdl,30);When you construct an IRF of a regression model with ARIMA errors containing a regression component, do not specify the predictor matrix, X, in filter.
Plot the IRFs.
figure tiledlayout(2,1) nexttile stem((0:numel(yFltr)-1)',yFltr,"filled") title("Impulse Response to Shock of One Standard Deviation") nexttile stem((0:numel(yImpls)-1)',yImpls,"filled") title("Impulse Response to Unit Shock")
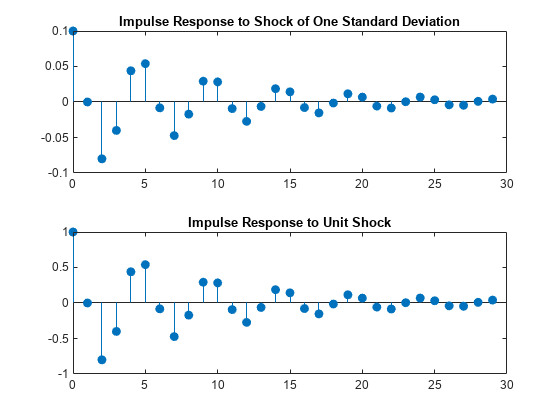
The IRF given a shock of one standard deviation is a scaled version of the IRF returned by impulse.
Compute the step response function of a regression model with ARMA(2,1) errors.
The step response assesses the dynamic behavior of a system to a persistent shock. Typically, the magnitude of the shock is 1. Alternatively, it might be more meaningful to examine a step response of a persistent innovation shock with a magnitude of one standard deviation. This example plots the step response of a persistent innovations shock in a model without an intercept and predictor matrix for regression. However, note that filter is flexible in that it accepts a persistent innovations or predictor shock that you construct using any magnitude, then filters it through the model.
Specify the following regression model with ARMA(2,1) errors:
where is Gaussian with variance 0.1.
Mdl = regARIMA(Intercept=0,AR={0.5 -0.8},MA=-0.5, ...
Variance=0.1);Compute the first 30 responses to a sequence of unit errors by generating an error series of one standard deviation, and then filtering it.
z = sqrt(Mdl.Variance)*ones(30,1); % Persistent shock of one std y = filter(Mdl,z); y = y/y(1); % Normalize relative to y(1)
Plot the step response function.
figure stem((0:numel(y)-1)',y,"filled") title("Step Response for Persistent Shock of One STD")
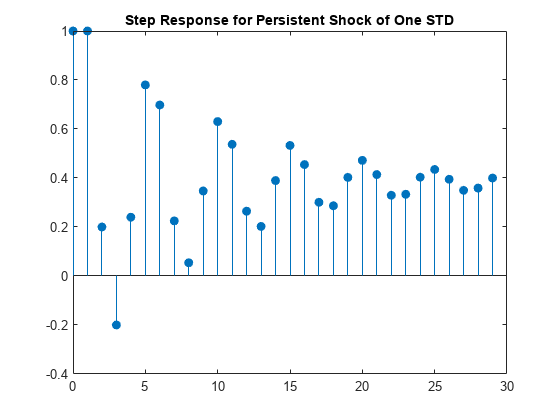
The step response settles around 0.4.
Fit a regression model with ARMA(1,1) errors by regressing the US consumer price index (CPI) quarterly changes onto the US gross domestic product (GDP) growth rate. Supply a timetable of data and specify the series for the fit. Then, filter paths of disturbances in a timetable through the fitted model.
Load and Transform Data
Load the US macroeconomic data set. Compute the series of GDP quarterly growth rates and CPI quarterly changes.
load Data_USEconModel DTT = price2ret(DataTimeTable,DataVariables="GDP"); DTT.GDPRate = 100*DTT.GDP; DTT.CPIDel = diff(DataTimeTable.CPIAUCSL); T = height(DTT)
T = 248
figure tiledlayout(2,1) nexttile plot(DTT.Time,DTT.GDPRate) title("GDP Rate") ylabel("Percent Growth") nexttile plot(DTT.Time,DTT.CPIDel) title("Index")
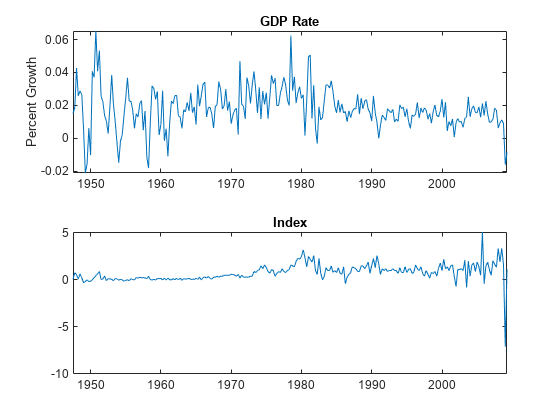
The series appear stationary, albeit heteroscedastic.
Prepare Timetable for Estimation
When you plan to supply a timetable, you must ensure it has all the following characteristics:
The selected response variable is numeric and does not contain any missing values.
The timestamps in the
Timevariable are regular, and they are ascending or descending.
Remove all missing values from the timetable.
DTT = rmmissing(DTT); T_DTT = height(DTT)
T_DTT = 248
Because each sample time has an observation for all variables, rmmissing does not remove any observations.
Determine whether the sampling timestamps have a regular frequency and are sorted.
areTimestampsRegular = isregular(DTT,"quarters")areTimestampsRegular = logical
0
areTimestampsSorted = issorted(DTT.Time)
areTimestampsSorted = logical
1
areTimestampsRegular = 0 indicates that the timestamps of DTT are irregular. areTimestampsSorted = 1 indicates that the timestamps are sorted. Macroeconomic series in this example are timestamped at the end of the month. This quality induces an irregularly measured series.
Remedy the time irregularity by shifting all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt; areTimestampsRegular = isregular(DTT,"quarters")
areTimestampsRegular = logical
1
DTT is regular.
Create Model Template for Estimation
Suppose that a regression model of CPI quarterly changes onto the GDP rate, with ARMA(1,1) errors, is appropriate.
Create a model template for a regression model with ARMA(1,1) errors template.
Mdl = regARIMA(1,0,1)
Mdl =
regARIMA with properties:
Description: "ARMA(1,1) Error Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
Intercept: NaN
Beta: [1×0]
P: 1
Q: 1
AR: {NaN} at lag [1]
SAR: {}
MA: {NaN} at lag [1]
SMA: {}
Variance: NaN
Mdl is a partially specified regARIMA object.
Fit Model to Data
Fit a regression model with ARMA(1,1) errors to the data. Specify the entire series GDP rate and CPI quarterly changes series, and specify the response and predictor variable names.
EstMdl = estimate(Mdl,DTT,ResponseVariable="GDPRate", ... PredictorVariables="CPIDel");
Regression with ARMA(1,1) Error Model (Gaussian Distribution):
Value StandardError TStatistic PValue
________ _____________ __________ __________
Intercept 0.0162 0.0016077 10.077 6.9995e-24
AR{1} 0.60515 0.089912 6.7305 1.6906e-11
MA{1} -0.16221 0.11051 -1.4678 0.14216
Beta(1) 0.002221 0.00077691 2.8587 0.0042532
Variance 0.000113 7.2753e-06 15.533 2.0838e-54
EstMdl is a fully specified, estimated regARIMA object.
Filter Random Gaussian Disturbance Paths
Generate 2 random, independent series of length T_DTT from the standard Gaussian distribution. Store the matrix of series as one variable in DTT.
rng(1,"twister") % For reproducibility DTT.Z = randn(T_DTT,2);
DTT contains a new variable called Z containing a T_DTT-by-2 matrix of two disturbance paths.
Filter the paths of disturbances through the estimated model. Specify the table variable name containing the disturbance paths.
Tbl2 = filter(EstMdl,DTT,DisturbanceVariable="Z");
tail(Tbl2) Time Interval GDP GDPRate CPIDel Z Y_Response Y_ErrorInnovation Y_RegressionInnovation
_____ ________ ___________ __________ ______ ______________________ ______________________ __________________________ __________________________
Q2-07 91 0.00018278 0.018278 1.675 -0.36436 -0.7055 0.016068 0.0071243 -0.0038733 -0.0074997 -0.0001316 -0.0090757
Q3-07 91 0.00016916 0.016916 1.359 -0.093312 -0.3311 0.015757 0.0084046 -0.00099194 -0.0035197 -0.00044331 -0.0077954
Q4-07 94 6.1286e-05 0.0061286 3.355 0.48981 -1.5208 0.021299 -0.0041131 0.0052068 -0.016167 0.0050995 -0.020313
Q1-08 91 9.3272e-05 0.0093272 1.93 1.4014 0.16528 0.033339 0.0082868 0.014898 0.001757 0.017139 -0.0079132
Q2-08 91 0.00011103 0.011103 3.367 -0.27422 -0.48787 0.02124 0.00594 -0.0029151 -0.0051862 0.0050402 -0.01026
Q3-08 92 8.9585e-05 0.0089585 1.641 0.67582 0.58697 0.026907 0.017072 0.0071842 0.0062397 0.010707 0.00087209
Q4-08 92 -0.00016145 -0.016145 -7.098 0.19058 -0.90337 0.02354 0.0061124 0.0020259 -0.0096032 0.00734 -0.010088
Q1-09 90 -8.6878e-05 -0.0086878 1.137 0.67036 0.37101 0.027439 0.015597 0.0071262 0.003944 0.011239 -0.00060284
size(Tbl2)
ans = 1×2
248 8
Tbl2 is a 248-by-8 timetable containing all variables in DTT, and the two filtered response paths Y_Response, error model innovation paths Y_ErrorInnovation, and unconditional disturbance paths Y_RegressionInnovation.
Simulate 100 independent paths of responses by filtering 100 independent paths of errors , where innovations , through the following regression model with SARIMA errors.
where follows a -distribution with 15 degrees of freedom.
Distribution = struct("Name","t","DoF",15); Mdl = regARIMA(AR={0.2 0.1},SAR=0.01,SARLags=12, ... MA=0.5,SMA=0.02,SMALags=12,D=1,Seasonality=12, ... Beta=[1.5; -2],Intercept=0,Variance=0.1, ... Distribution=Distribution)
Mdl =
regARIMA with properties:
Description: "Regression with ARIMA(2,1,1) Error Model Seasonally Integrated with Seasonal AR(12) and MA(12) (t Distribution)"
SeriesName: "Y"
Distribution: Name = "t", DoF = 15
Intercept: 0
Beta: [1.5 -2]
P: 27
D: 1
Q: 13
AR: {0.2 0.1} at lags [1 2]
SAR: {0.01} at lag [12]
MA: {0.5} at lag [1]
SMA: {0.02} at lag [12]
Seasonality: 12
Variance: 0.1
Simulate a length 25 path of data from the standard bivariate normal distribution for the predictor variables in the regression component.
rng(1,"twister") % For reproducibility numObs = 25; Pred = randn(numObs,2);
Simulate 100 independent paths of errors of length 25 from the standard normal distribution.
numPaths = 100; Z = randn(numObs,numPaths);
Simulate 100 independent response paths from model by filtering the paths of errors through the model. Supply the predictor data for the regression component.
Y = filter(Mdl,Z,X=Pred);
figure
plot(Y)
title("Simulated Response Paths")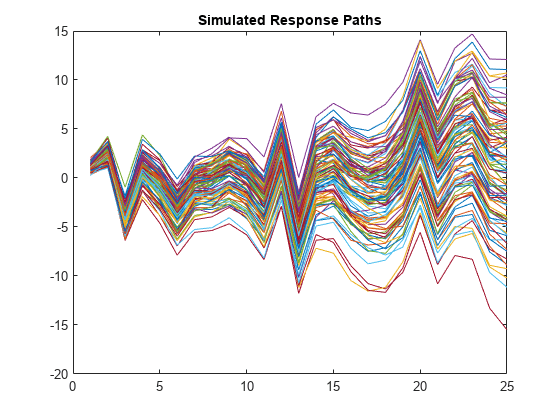
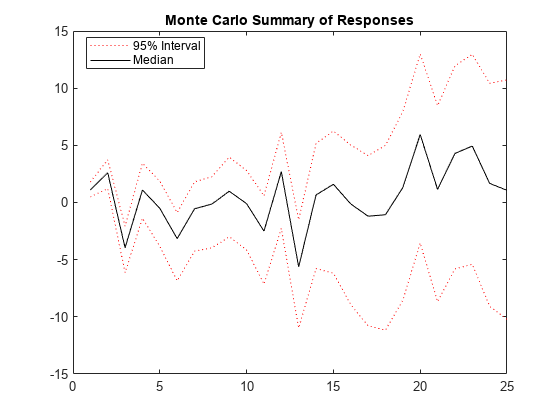
Plot the 2.5th, 50th (median), and 97.5th percentiles of the simulated response paths.
lower = prctile(Y,2.5,2); middle = median(Y,2); upper = prctile(Y,97.5,2); figure plot(1:25,lower,"r:",1:25,middle,"k", ... 1:25,upper,"r:") title("Monte Carlo Summary of Responses") legend("95% Interval","Median",Location="best")
Simulate responses using filter and simulate. Then compare the simulated responses.
Both filter and simulate filter a series of errors to produce output responses y, innovations e, and unconditional disturbances u. The difference is that simulate generates errors from Mdl.Distribution, whereas filter accepts a random array of errors that you generate from any distribution.
Specify the following regression model with ARMA(2,1) errors:
where is Gaussian with variance 0.1.
Mdl = regARIMA(Intercept=0,AR={0.5 -0.8},MA=-0.5, ...
Beta=[0.1 -0.2],Variance=0.1);Mdl is a fully specified regARIMA object.
Simulate a one path of bivariate standard normal data for the predictor variables. Then, simulate a path of responses and innovations from the regression model with ARMA(2,1) errors. Supply the simulated predictor data to simulate for the regression component.
rng(1,"twister") % For reproducibility Pred = randn(100,2); % Simulate predictor data [ySim,eSim] = simulate(Mdl,100,X=Pred);
ySim and eSIM are 100-by-1 vectors of simulated responses and innovations, respectively, from the model Mdl.
Produce model errors by standardizing the simulated innovations. Filter the simulated errors through the model. Supply the predictor data to filter.
z1 = eSim./sqrt(Mdl.Variance); yFlt1 = filter(Mdl,z1,X=Pred);
yFlt1 is a 100-by-1 vector of responses resulting from filtering the simulated errors z1 through the model Mdl.
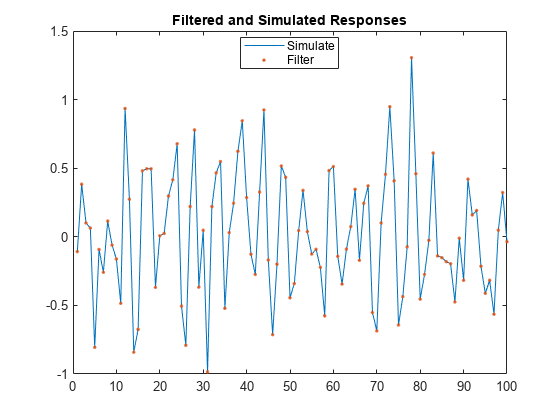
Confirm that the simulated responses from simulate and filter are identical by plotting the two series.
figure h1 = plot(ySim); hold on h2 = plot(yFlt1,"."); title("Filtered and Simulated Responses") legend([h1 h2],["Simulate" "Filter"],Location="best") hold off
Alternatively, simulate responses by randomly generating your own errors and passing them into filter.
rng(1,"twister") Pred = randn(100,2); z2 = randn(100,1); yFlt2 = filter(Mdl,z2,X=Pred); figure h1 = plot(ySim); hold on h2 = plot(yFlt2,"."); title("Filtered and Simulated Responses") legend([h1 h2],["Simulate" "Filter"],Location="best") hold off
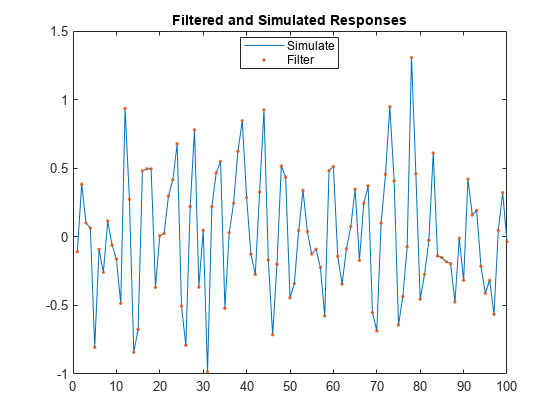
This plot is the same as the previous plot, confirming that both simulation methods are equivalent.
filter multiplies the error, Z, by sqrt(Mdl.Variance) before filtering Z through the model. Therefore, if you want to specify a different distribution, set Mdl.Variance to 1, and then generate your own errors using, for example, random("unif",a,b) for the Uniform(a, b) distribution.
Input Arguments
Error model disturbance series zt that
drives the error model innovations process εt,
specified as a numobs-by-1 numeric column vector or a
numobs-by-numpaths numeric matrix.
numobs is the length of the time series (sample size).
numpaths is the number of separate, independent disturbance paths.
The innovations process εt =
σzt, where σ =
sqrt(Mdl.Variance), the standard deviation of the
innovations.
Each row corresponds to a sampling time. The last row contains the latest set of disturbances.
Each column corresponds to a separate, independent path of error model disturbances.
filter assumes that disturbances across any row occur
simultaneously.
Z is the continuation of the presample disturbances
Z0.
Data Types: double
Since R2023b
Time series data containing the error model disturbance series
zt that drives the error model innovations
process εt, and, optionally, predictor
variables xt, specified as a table or
timetable with numvars variables and numobs rows.
You can optionally select the disturbance variable or numpreds
predictor variables by using the DisturbanceVariable or
PredictorVariables name-value arguments, respectively. The
innovations process εt =
σzt, where σ =
sqrt(Mdl.Variance), the standard deviation of the
innovations.
Each row is an observation, and measurements in each row occur simultaneously. The
selected disturbance variable is a single path (numobs-by-1 vector)
or multiple paths (numobs-by-numpaths matrix) of
numobs observations of disturbance data.
Each path (column) of the selected disturbance variable is independent of the other
paths, but path jjnumpaths. Each selected predictor variable is a
numobs-by-1 numeric vector representing one path. The
filter function includes all predictor variables in the
model when it filters each disturbance path. Variables in Tbl1
represent the continuation of corresponding variables in
Presample.
If Tbl1 is a timetable, it must represent a sample with a
regular datetime time step (see isregular), and the datetime vector Tbl1.Time must be
strictly ascending or descending.
If Tbl1 is a table, the last row contains the latest
observation.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: filter(Mdl,Z,X=Pred,Z0=PSZ) specifies the predictor data
Pred for the model regression component and the observed errors in
the presample period PSZ to initialize the model.
Since R2023b
Disturbance variable zt to select from
Tbl1 containing the disturbance data to filter through
Mdl, specified as one of the following data types:
String scalar or character vector containing a variable name in
Tbl1.Properties.VariableNamesVariable index (positive integer) to select from
Tbl1.Properties.VariableNamesA logical vector, where
DisturbanceVariable(selects variablej) = truejTbl1.Properties.VariableNames
The selected variable must be a numeric vector and cannot contain missing values
(NaNs).
If Tbl1 has one variable, the default specifies that variable.
Otherwise, the default matches the variable to names in
Mdl.SeriesName.
Example: DisturbanceVariable="StockRateDist"
Example: DisturbanceVariable=[false false true false] or
DisturbanceVariable=3 selects the third table variable as the
disturbance variable.
Data Types: double | logical | char | cell | string
Predictor data for the model regression component, specified as a
numobs-by-numpreds numeric matrix.
numpreds is the number of predictor variables
(numel(Mdl.Beta)). Use X only when you supply
the numeric array of disturbance data Z.
X must have at least numobs rows. The last
row contains the latest predictor data. If X has more than
numobs rows, filter uses only the
latest numobs rows. Each row of X corresponds to
each period in Z (period for which
filter filters errors; the period after the
presample).
filter does not use the regression component in the
presample period.
Columns of X are separate predictor variables.
filter applies X to each filtered
path; that is, X represents one path of observed predictors.
By default, filter excludes the regression component,
regardless of its presence in Mdl.
Data Types: double
Predictor variables xt to select from
Tbl1 containing the predictor data for the model regression
component, specified as one of the following data types:
String vector or cell vector of character vectors containing
numpredsvariable names inTbl1.Properties.VariableNamesA vector of unique indices (positive integers) of variables to select from
Tbl1.Properties.VariableNamesA logical vector, where
PredictorVariables(selects variablej) = truejTbl1.Properties.VariableNames
The selected variables must be numeric vectors and cannot contain missing values (NaNs).
By default, filter excludes the regression component, regardless of its presence in Mdl.
Example: PredictorVariables=["M1SL" "TB3MS" "UNRATE"]
Example: PredictorVariables=[true false true false] or PredictorVariable=[1 3] selects the first and third table variables to supply the predictor data.
Data Types: double | logical | char | cell | string
Presample disturbance data zt to
initialize the error model, specified as a numpreobs-by-1 numeric
column vector or a numpreobs-by-numprepaths
numeric matrix. Use Z0 only when you supply the numeric array of
disturbance data Z.
Each row is a presample observation (sampling time), and measurements in each row
occur simultaneously. The last row contains the latest presample observation.
numpreobs must be at least Mdl.Q to initialize
the error model moving average (MA) component. If numpreobs is
larger than required, filter uses the latest required
observations only.
Columns of Z0 are separate, independent presample paths. The
following conditions apply:
If
Z0is a column vector, it represents a single disturbance path.filterapplies it to each output path.If
Z0is a matrix, each column represents a presample disturbance path.filterappliesZ0(:,to initialize pathj)j.numprepathsmust be at leastnumpaths. Ifnumprepaths>numpaths,filteruses the firstsize(Z,2)columns only.
By default, filter sets the necessary presample
disturbances to zero.
Data Types: double
Presample regression innovation data (unconditional disturbances)
ut to initialize the error model,
specified as a numpreobs-by-1 numeric column vector or a
numpreobs-by-numprepaths numeric matrix. Use
U0 only when you supply the numeric array of disturbance data
Z.
Each row is a presample observation (sampling time), and measurements in each row
occur simultaneously. The last row contains the latest presample observation.
numpreobs must be at least Mdl.P to initialize
the error model autoregressive (AR) component. If numpreobs is
larger than required, filter uses the latest required
observations only.
Columns of U0 are separate, independent presample paths. The
following conditions apply:
If
U0is a column vector, it represents a single path.filterapplies it to each path.If
U0is a matrix, each column represents a presample path.filterappliesU0(:,to initialize pathj)j.numprepathsmust be at leastnumpaths. Ifnumprepaths>numpaths,filteruses the firstsize(Z,2)columns only.
By default, filter sets the necessary presample
unconditional disturbances to 0.
Data Types: double
Since R2023b
Presample data containing paths of disturbance
zt or regression innovation (unconditional
disturbance) ut series to initialize the
model, specified as a table or timetable, the same type as Tbl1,
with numprevars variables and numpreobs rows.
Use Presample only when you supply a table or timetable of data
Tbl1.
Each selected variable is a single path (numpreobs-by-1 vector)
or multiple paths (numpreobs-by-numprepaths
matrix) of numpreobs observations representing the presample of the
error model disturbance or regression innovation series for
DisturbanceVariable, the selected error model disturbance
variable in Tbl1.
Each row is a presample observation, and measurements in each row occur
simultaneously. numpreobs must be one of the following values:
At least
Mdl.PwhenPresampleprovides only presample regression innovations to initialize the error model AR componentAt least
Mdl.QwhenPresampleprovides only presample error model disturbances to initialize the error model MA componentAt least
max([Mdl.P Mdl.Q])otherwise
If you supply more rows than necessary, filter uses the
latest required number of observations only.
If Presample is a timetable, all the following conditions
must be true:
Presamplemust represent a sample with a regular datetime time step (seeisregular).The inputs
Tbl1andPresamplemust be consistent in time such thatPresampleimmediately precedesTbl1with respect to the sampling frequency and order.The datetime vector of sample timestamps
Presample.Timemust be ascending or descending.
If Presample is a table, the last row contains the latest
presample observation.
By default, filter sets necessary presample error model
disturbances and regression innovations to zero.
If you specify the Presample, you must specify the presample
error model disturbance or regression innovation variable name by using the
PresampleDisturbanceVariable or
PresampleRegressionDisturbanceVariable name-value
argument.
Since R2023b
Error model disturbance variable zt to
select from Presample containing the presample error model
disturbance data, specified as one of the following data types:
String scalar or character vector containing the variable name to select from
Presample.Properties.VariableNamesVariable index (positive integer) to select from
Presample.Properties.VariableNamesA logical vector, where
PresampleDisturbanceVariable(selects variablej) = truejPresample.Properties.VariableNames
The selected variable must be a numeric vector and cannot contain missing values
(NaNs).
If you specify presample error model disturbance data by using the
Presample name-value argument, you must specify
PresampleDisturbanceVariable.
Example: PresampleDisturbanceVariable="GDP_Z"
Example: PresampleDisturbanceVariable=[false false true false]
or PresampleDisturbanceVariable=3 selects the third table variable
for presample error model disturbance data.
Data Types: double | logical | char | cell | string
Since R2023b
Regression model innovation variable, associated with unconditional disturbances
ut, to select from
Presample containing data for the presample regression model
innovations, specified as one of the following data types:
String scalar or character vector containing a variable name in
Presample.Properties.VariableNamesVariable index (positive integer) to select from
Presample.Properties.VariableNamesA logical vector, where
PresampleRegressionDisturbanceVariable(selects variablej) = truejPresample.Properties.VariableNames
The selected variable must be a numeric vector and cannot contain missing values
(NaNs).
If you specify presample regression model innovation data by using the
Presample name-value argument, you must specify
PresampleRegressionDisturbanceVariable.
Example: PresampleRegressionDisturbanceVariable="StockRateU"
Example: PresampleRegressionDisturbanceVariable=[false false true
false] or PresampleRegressionDisturbanceVariable=3
selects the third table variable as the presample regression model innovation
data.
Data Types: double | logical | char | cell | string
Note
NaNvalues inZ,X,Z0andU0indicate missing values.filterremoves missing values from specified data by listwise deletion.For the presample,
filterhorizontally concatenates the possibly jagged arraysZ0andU0with respect to the last rows, and then it removes any row of the concatenated matrix containing at least oneNaN.For in-sample data,
filterhorizontally concatenates the possibly jagged arraysZandX, and then it removes any row of the concatenated matrix containing at least oneNaN.
This type of data reduction reduces the effective sample size and can create an irregular time series.
For numeric data inputs,
filterassumes that you synchronize the presample data such that the latest observations occur simultaneously.filterissues an error when any table or timetable input contains missing values.All predictor variables (columns) in
Xare associated with each input error series to producenumpathsoutput series.
Output Arguments
Simulated response paths yt, returned as a
numobs-by-1 column vector or a
numobs-by-numpaths numeric matrix.
filter returns Y only when you supply
the input Z.
For each tnumobs, the simulated responses at time
tY( correspond to the filtered errors
at time t,:)tZ( and response path
t,:)jY(:, corresponds to the filtered
disturbance path j)jZ(:, when j)Z is a
matrix.
Y represents the continuation of presample inputs.
Simulated, mean-zero innovations paths εt
of the error model, returned as a numobs-by-1 column vector or a
numobs-by-numpaths numeric matrix.
filter returns E only when you supply
the input Z.
The dimensions of Y and E correspond.
Columns of E are scaled disturbance paths (innovations) such
that, for a particular path, εt =
σzt.
Since R2023b
Simulated response yt, error model
innovation εt, and unconditional disturbance
ut paths, returned as a table or
timetable, the same data type as Tbl1.
filter returns Tbl2 only when you
supply the input Tbl1.
Tbl2 contains the following variables:
The filtered response paths, which are in a
numobs-by-numpathsnumeric matrix, with rows representing observations and columns representing independent paths, each corresponding to the input observations and paths of the error model disturbance variable inTbl1.filternames the simulated response variable inTbl2responseName_ResponseresponseNameMdl.SeriesName. For example, ifMdl.SeriesNameisStockReturns,Tbl2contains a variable for the corresponding simulated response paths with the nameStockReturns_Response.The simulated error model innovation paths, which are in a
numobs-by-numpathsnumeric matrix, with rows representing observations and columns representing independent paths, each corresponding to the input observations and paths of the error model disturbance variable inTbl1.filternames the simulated error model innovation variable inTbl2responseName_ErrorInnovationresponseNameMdl.SeriesName. For example, ifMdl.SeriesNameisStockReturns,Tbl2contains a variable for the corresponding simulated error model innovation paths with the nameStockReturns_ErrorInnovation.The simulated unconditional disturbance paths, which are in a
numobs-by-numpathsnumeric matrix, with rows representing observations and columns representing independent paths, each corresponding to the input observations and paths of the error model disturbance variable inTbl1.filternames the simulated unconditional disturbance variable inTbl2responseName_RegressionInnovationresponseNameMdl.SeriesName. For example, ifMdl.SeriesNameisStockReturns,Tbl2contains a variable for the corresponding simulated unconditional disturbance paths with the nameStockReturns_RegressionInnovation.All variables
Tbl1.
If Tbl1 is a timetable, row times of Tbl1
and Tbl2 are equal.
Alternative Functionality
filter generalizes simulate. Both filter a series of errors to produce responses
Y, innovations E, and unconditional disturbances
U. However, simulate autogenerates
a series of mean zero, unit variance, independent and identically distributed (iid) errors
according to the distribution in Mdl. In contrast,
filter requires that you specify your own errors, which can come
from any distribution.
References
[1] Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.
[2] Davidson, R., and J. G. MacKinnon. Econometric Theory and Methods. Oxford, UK: Oxford University Press, 2004.
[3] Enders, Walter. Applied Econometric Time Series. Hoboken, NJ: John Wiley & Sons, Inc., 1995.
[4] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[5] Pankratz, A. Forecasting with Dynamic Regression Models. John Wiley & Sons, Inc., 1991.
[6] Tsay, R. S. Analysis of Financial Time Series. 2nd ed. Hoboken, NJ: John Wiley & Sons, Inc., 2005.
Version History
Introduced in R2013bIn addition to accepting input data (in-sample and presample data) in numeric arrays,
filter accepts input data in tables or regular timetables. When
you supply data in a table or timetable, the following conditions apply:
filterchooses the default in-sample error model disturbance series on which to operate, but you can use the specified optional name-value argument to select a different series.If you specify optional presample error model disturbance or regression model innovation data to initialize the model, you must also specify the appropriate presample variable names.
filterreturns results in a table or timetable.
Name-value arguments to support tabular workflows include:
DisturbanceVariablespecifies the name of the disturbance series in the input data to filter through the model.PredictorVariablesspecifies the names of the predictor series to select from the input data for the model regression component.Presamplespecifies the input table or timetable of presample error model disturbance or regression innovation data.PresampleDisturbanceVariablespecifies the name of the error model disturbance series to select fromPresample.PresampleRegressionDisturbanceVariablespecifies the name of the regression model innovation series to select fromPresample.
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)