estimate
Syntax
Description
EstMdl = estimate(Mdl,tt0,Y)Mdl. estimate fits the model to the response
data Y, and initializes the estimation procedure by treating the
parameter values of the fully specified threshold transitions tt0 as
initial values. estimate implements a version of the conditional
least-squares algorithm described in [4].
EstMdl = estimate(Mdl,tt0,Y,Name,Value)estimate(Mdl,tt0,Y,IterationPlot=true)
displays a plot of the loglikelihood versus the iteration step, after the algorithm
terminates.
Examples
Assess estimation accuracy using simulated data from a known data-generating process (DGP). This example uses arbitrary parameter values.
Create Model for DGP
Create a discrete threshold transition at mid-level 1.
ttDGP = threshold(1)
ttDGP =
threshold with properties:
Type: 'discrete'
Levels: 1
Rates: []
StateNames: ["1" "2"]
NumStates: 2
ttDGP is a threshold object representing the state-switching mechanism of the DGP.
Create the following fully specified self-exciting TAR (SETAR) model for the DGP.
State 1: .
State 2: .
.
Specify the submodels by using arima.
mdl1DGP = arima(Constant=0); mdl2DGP = arima(Constant=2); mdlDGP = [mdl1DGP mdl2DGP];
Because the innovations distribution is invariant across states, the tsVAR software ignores the value of the submodel innovations variance (Variance property).
Create a threshold-switching model for the DGP. Specify the model-wide innovations variance.
MdlDGP = tsVAR(ttDGP,mdlDGP,Covariance=1);
MdlDGP is a tsVAR object representing the DGP.
Simulate Response Paths from DGP
Generate a random response path of length 100 from the DGP. By default, simulate assumes a SETAR model with delay . In other words, the threshold variable is .
rng(1) % For reproducibiliy
y = simulate(MdlDGP,100);y is a 100-by-1 vector of representing the simulated response path.
Create Model for Estimation
Create a partially specified threshold-switching model that has the same structure as the data-generating process, but specify the transition mid-level, submodel coefficients, and model-wide constant as unknown for estimation.
tt = threshold(NaN); mdl1 = arima('Constant',NaN); mdl2 = arima('Constant',NaN); Mdl = tsVAR(tt,[mdl1,mdl2],'Covariance',NaN);
Mdl is a partially specified tsVAR object representing a template for estimation. NaN-valued elements of the Switch and Submodels properties indicate estimable parameters.
Mdl is agnostic of the threshold variable; tsVAR object functions enable you to specify threshold variable characteristics or data.
Create Threshold Transitions Containing Initial Values
The estimation procedure requires initial values for all estimable threshold transition parameters.
Fully specify a threshold transition that has the same structure as tt, but set the mid-level to 0.
tt0 = threshold(0);
tt0 is a fully specified threshold object.
Estimate Model
Fit the model to the simulated path. By default, the model is self-exciting and the delay of the threshold variable is .
EstMdl = estimate(Mdl,tt0,y)
EstMdl =
tsVAR with properties:
Switch: [1×1 threshold]
Submodels: [2×1 varm]
NumStates: 2
NumSeries: 1
StateNames: ["1" "2"]
SeriesNames: "1"
Covariance: 1.0225
EstMdl is a fully specified tsVAR object representing the estimated SETAR model.
Display an estimation summary of the submodels.
summarize(EstMdl)
Description
1-Dimensional tsVAR Model with 2 Submodels
Switch
Transition Type: discrete
Estimated Levels: 1.128
Fit
Effective Sample Size: 99
Number of Estimated Parameters: 2
Number of Constrained Parameters: 0
LogLikelihood: -141.574
AIC: 287.149
BIC: 292.339
Submodels
Estimate StandardError TStatistic PValue
________ _____________ __________ __________
State 1 Constant(1) -0.12774 0.13241 -0.96474 0.33467
State 2 Constant(1) 2.1774 0.16829 12.939 2.7264e-38
The estimates are close to their true values.
Plot the estimated switching mechanism with the threshold data, which is the response data.
figure
ttplot(EstMdl.Switch,'Data',y)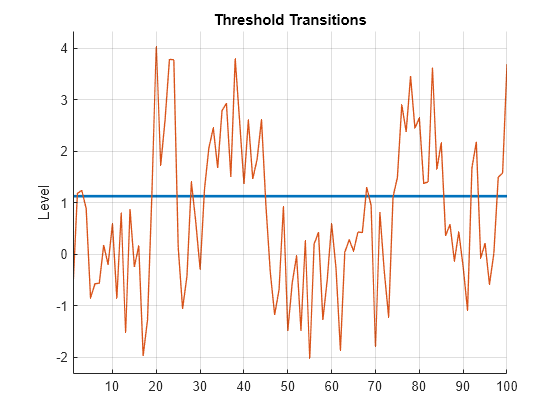
estimate does not fit the delay parameter to the data; you must specify its value when you call estimate. This example shows how to tune .
Create the following fully specified SETAR model for the DGP.
State 1: , where .
State 2: , where .
The system is in state 1 when , and it is in state 2 otherwise.
ttDGP = threshold(0); mdl1DGP = arima(Constant=0,Variance=1); mdl2DGP = arima(Constant=2,Variance=2); mdlDGP = [mdl1DGP; mdl2DGP]; MdlDGP = tsVAR(ttDGP,mdlDGP);
Generate a random response path of length 200 from the DGP. Specify that the threshold variable delay is 4.
rng(1) % For reproducibiliy
y = simulate(MdlDGP,200,Delay=4);
plot(y)
Create a partially specified threshold-switching model that has the same structure as the data-generating process, but specify the transition mid-level, submodel coefficients, and state-specific variances as unknown for estimation.
tt = threshold(NaN); mdl = arima(0,0,0); Mdl = tsVAR(tt,[mdl; mdl]);
Fully specify a threshold transition that has the same structure as tt, but set the mid-level to 0.5.
tt0 = threshold(0.5);
Tune by choosing a set of plausible values for it, and by fitting the SETAR model to the simulated data for each value in the set. Choose the model that maximizes the loglikelihood.
d = 1:8; nd = numel(d); logL = zeros(nd,1); % Preallocate for loglikelihoods EstMdl = cell(nd,1); % Preallocate for estimated models for j = 1:nd [EstMdl{j},logL(j)] = estimate(Mdl,tt0,y,Delay=d(j)); end
Extract the model that maximizes the loglikelihood.
[~,optDelay] = max(logL)
optDelay = 4
OptEstMdl = EstMdl{optDelay};The optimal delay is 4, which matches the delay of the DGP.
Display an estimation summary of the optimal model, and display its estimated switching mechanism.
summarize(OptEstMdl)
Description
1-Dimensional tsVAR Model with 2 Submodels
Switch
Transition Type: discrete
Estimated Levels: -0.063
Fit
Effective Sample Size: 196
Number of Estimated Parameters: 2
Number of Constrained Parameters: 0
LogLikelihood: -336.184
AIC: 676.367
BIC: 682.923
Submodels
Estimate StandardError TStatistic PValue
________ _____________ __________ __________
State 1 Constant(1) -0.33535 0.24271 -1.3817 0.16707
State 2 Constant(1) 2.0073 0.10647 18.853 2.7794e-79
The estimates are close to the parameters of the DGP.
Create the following fully specified SETAR model for the DGP.
State 1: .
State 2: .
State 3:.
.
The system is in state 1 when , the system is in state 2 when 3, and the system is in state 3 otherwise.
t = [-3 3];
ttDGP = threshold(t);
constant1 = [-1; -4];
constant2 = [1; 4];
constant3 = [1; 4];
AR1 = [-0.5 0.1; 0.2 -0.75];
AR3 = [0.5 0.1; 0.2 0.75];
Sigma = [2 -1; -1 1];
mdl1DGP = varm(Constant=constant1,AR={AR1});
mdl2DGP = varm(Constant=constant2);
mdl3DGP = varm(Constant=constant3,AR={AR3});
mdlDGP = [mdl1DGP; mdl2DGP; mdl3DGP];
MdlDGP = tsVAR(ttDGP,mdlDGP,Covariance=Sigma);Generate a random response path of length 500 from the DGP. Specify that second response variable with a delay of 4 as the threshold variable.
rng(10) % For reproducibiliy
y = simulate(MdlDGP,500,Index=2,Delay=4);Create a partially specified threshold-switching model that has the same structure as the DGP, but specify the transition mid-level, submodel coefficients, and model-wide covariance as unknown for estimation.
tt = threshold([NaN; NaN]); mdlar = varm(2,1); mdlc = varm(2,0); Mdl = tsVAR(tt,[mdlar; mdlc; mdlar],Covariance=nan(2));
Fully specify a threshold transition that has the same structure as tt, but set the mid-levels to -1 and 1.
t0 = [-1 1]; tt0 = threshold(t0);
Fit the threshold-switching model to the simulated series. Specify the threshold variable . Plot the loglikelihood after each iteration of the threshold search algorithm.
EstMdl = estimate(Mdl,tt0,y,IterationPlot=true,Index=2,Delay=4);

The plot displays the evolution of the loglikelihood as the estimation procedure searches for optimal levels. The procedure terminates when one of the stopping criteria is satisfied.
Display an estimation summary of the model.
summarize(EstMdl)
Description
2-Dimensional tsVAR Model with 3 Submodels
Switch
Transition Type: discrete
Estimated Levels: -2.877 2.991
Fit
Effective Sample Size: 496
Number of Estimated Parameters: 14
Number of Constrained Parameters: 0
LogLikelihood: -1478.416
AIC: 2984.831
BIC: 3043.723
Submodels
Estimate StandardError TStatistic PValue
________ _____________ __________ ___________
State 1 Constant(1) -1.0369 0.13859 -7.4821 7.312e-14
State 1 Constant(2) -4.0179 0.09959 -40.345 0
State 1 AR{1}(1,1) -0.43289 0.063204 -6.8491 7.4332e-12
State 1 AR{1}(2,1) 0.20344 0.045419 4.4791 7.4957e-06
State 1 AR{1}(1,2) 0.076123 0.024477 3.1099 0.0018714
State 1 AR{1}(2,2) -0.75607 0.01759 -42.983 0
State 2 Constant(1) 1.0545 0.14882 7.0858 1.382e-12
State 2 Constant(2) 4.1131 0.10694 38.46 1.9763e-323
State 3 Constant(1) 1.0621 0.095701 11.098 1.2802e-28
State 3 Constant(2) 3.8707 0.068772 56.284 0
State 3 AR{1}(1,1) 0.47396 0.058016 8.1694 3.0997e-16
State 3 AR{1}(2,1) 0.23013 0.041691 5.5199 3.3927e-08
State 3 AR{1}(1,2) 0.10561 0.018233 5.7924 6.9371e-09
State 3 AR{1}(2,2) 0.7568 0.013102 57.761 0
Consider a smooth threshold-switching (STAR) model for the real US GDP growth rate, where each submodel is AR(4) and the threshold variable is the unemployment growth rate.
Create a partially specified threshold transition for the unemployment growth rate. Specify the normal cdf transition function, and an unknown, estimable mid-level and rate. Label the states "Contraction" and "Expansion".
tt = threshold(NaN,Type="normal",Rates=NaN, ... StateNames=["Contraction" "Expansion"]);
tt is a partially specified threshold object, and it is agnostic of the variable and data it represents.
Create a threshold-switching model for the real US GDP growth rate. Label the series "rRGDP".
mdl = arima(4,0,0);
submdls = [mdl; mdl];
Mdl = tsVAR(tt,submdls,SeriesNames="rRGDP");Load the quarterly US macroeconomic data set Data_USEconModel.mat. Compute the real GDP percent growth and unemployment growth.
load Data_USEconModel DataTimeTable = rmmissing(DataTimeTable,DataVariables=["GDP" "GDPDEF" "UNRATE"]); RGDP = DataTimeTable.GDP./DataTimeTable.GDPDEF; rRGDP = price2ret(RGDP)*100; % Response data gUNRATE = diff(DataTimeTable.UNRATE); % Exogenous thresold data dates = DataTimeTable.Time(2:end);
Suppose the estimation period includes growth rates from the first quarter of 1950. Identify the estimation period in the date base.
startEst = datetime(1950,1,1); idxEst = dates >= startEst;
To initialize the estimation procedure, fully specify a threshold transition that has the same structure as tt, but set the mid-level to -0.5 with a rate of 100.
tt0 = threshold(-0.5,Type=tt.Type,Rates=100,StateNames=tt.StateNames);
Fit the STAR model to the estimation period of the US GDP growth rate series. Specify the following parameters:
Set
Y0to the responses before the estimation period to initialize the AR submodel components.Set
Typeto "exogenous" to characterize the threshold variable.Set Z to the threshold variable data
gUNRATEin the estimation period.Set
MaxRateto150to expand the search for the optimal transition function rate.Plot the evolution of the loglikelihood.
EstMdl = estimate(Mdl,tt0,rRGDP(idxEst),Y0=rRGDP(~idxEst), ... Z=gUNRATE(idxEst),Type="exogenous",MaxRate=150,IterationPlot=true);

Display an estimation summary and plot the estimated switching mechanism with the threshold data.
summarize(EstMdl)
Description
1-Dimensional tsVAR Model with 2 Submodels
Switch
Transition Type: normal
Estimated Levels: 0.208
Estimated Rates: 75.566
Fit
Effective Sample Size: 237
Number of Estimated Parameters: 10
Number of Constrained Parameters: 0
LogLikelihood: -285.022
AIC: 590.043
BIC: 624.724
Submodels
Estimate StandardError TStatistic PValue
_________ _____________ __________ __________
State 1 Constant(1) 1.0473 0.11549 9.068 1.2125e-19
State 1 AR{1}(1,1) 0.15792 0.068783 2.2959 0.021679
State 1 AR{2}(1,1) 0.059888 0.066409 0.9018 0.36716
State 1 AR{3}(1,1) -0.10455 0.070384 -1.4854 0.13744
State 1 AR{4}(1,1) -0.098037 0.063249 -1.55 0.12114
State 2 Constant(1) -0.12491 0.15383 -0.81197 0.41681
State 2 AR{1}(1,1) 0.15366 0.13993 1.0981 0.27215
State 2 AR{2}(1,1) -0.027925 0.16754 -0.16667 0.86763
State 2 AR{3}(1,1) -0.24366 0.12778 -1.9068 0.056543
State 2 AR{4}(1,1) -0.075389 0.14024 -0.53759 0.59086
figure ttplot(EstMdl.Switch,Data=gUNRATE(idxEst)) dEst = dates(idxEst); xticklabels(string(dEst(xticks)))

The large rate suggests little mixing occurs between the models of each regime. When the quarterly unempoyment growth is less than 0.206%, the dominant model for the US GDP growth rate is in EstMdl.Submodels(1). Otherwise, the dominant submodel is in EstMdl.Submodels(2).
Many of the coefficients are insignificant, which can suggest a search for a simpler model.
This example shows how to specify equality constraints on estimable submodel coefficients and threshold parameters.
Consider the model for the real US GDP growth rate in Specify Presample Data for STAR Model Estimation. Assume the submodels are AR(4), but they include only the model constant (time trend in differenced series) and fourth lag. Also, suppose the transition function rate 3 for the unemployment growth series.
Create the partially specified threshold transition for the unemployment growth rate. Specify the known transition rate.
rConstraint = 3; tt = threshold(NaN,Type="normal",Rates=rConstraint, ... StateNames=["Contraction" "Expansion"]);
Create a threshold-switching model for the real US GDP growth rate. Explicitly specify the AR lags to include in the submodels by using the ARLags option.
mdl = arima(ARLags=4);
submdls = [mdl; mdl];
Mdl = tsVAR(tt,submdls,SeriesNames="rRGDP");Load the quarterly US macroeconomic data set Data_USEconModel.mat. Compute the real GDP percent growth and unemployment growth.
load Data_USEconModel DataTimeTable = rmmissing(DataTimeTable,DataVariables=["GDP" "GDPDEF" "UNRATE"]); RGDP = DataTimeTable.GDP./DataTimeTable.GDPDEF; rRGDP = price2ret(RGDP)*100; % Response data gUNRATE = diff(DataTimeTable.UNRATE); % Exogenous thresold data dates = DataTimeTable.Time(2:end);
Suppose the estimation period includes growth rates from the first quarter of 1950. Identify the estimation period in the date base.
startEst = datetime(1950,1,1); idxEst = dates >= startEst;
Fully specify a threshold transition that has the same structure as tt, including the equality constraint on the transition function rate. Set the initial mid-level to 0.
tt0 = threshold(0,Type=tt.Type,Rates=rConstraint,StateNames=tt.StateNames);
Fit the STAR model to the estimation period of the US GDP growth rate series. Specify the following parameters:
Set
Y0to the responses before the estimation period to initialize the AR submodel components.Set
Typeto"exogenous"to characterize the threshold variable.Set
Zto the threshold variable datagUNRATEin the estimation period.Set
MaxRateto 150 to expand the search for the optimal transition function rate.Plot the evolution of the loglikelihood.
EstMdl = estimate(Mdl,tt0,rRGDP(idxEst),Y0=rRGDP(~idxEst), ... Z=gUNRATE(idxEst),Type="exogenous",IterationPlot=true);

Display an estimation summary and plot the estimated switching mechanism with the threshold data.
summarize(EstMdl)
Description
1-Dimensional tsVAR Model with 2 Submodels
Switch
Transition Type: normal
Estimated Levels: 0.228
Estimated Rates: 3.000
Fit
Effective Sample Size: 237
Number of Estimated Parameters: 4
Number of Constrained Parameters: 6
LogLikelihood: -267.892
AIC: 543.784
BIC: 557.656
Submodels
Estimate StandardError TStatistic PValue
_________ _____________ __________ __________
State 1 Constant(1) 1.5928 0.087805 18.14 1.543e-73
State 1 AR{1}(1,1) 0 0 NaN NaN
State 1 AR{2}(1,1) 0 0 NaN NaN
State 1 AR{3}(1,1) 0 0 NaN NaN
State 1 AR{4}(1,1) -0.11789 0.067607 -1.7438 0.081194
State 2 Constant(1) -0.73667 0.15808 -4.6601 3.1609e-06
State 2 AR{1}(1,1) 0 0 NaN NaN
State 2 AR{2}(1,1) 0 0 NaN NaN
State 2 AR{3}(1,1) 0 0 NaN NaN
State 2 AR{4}(1,1) -0.040337 0.1299 -0.31053 0.75616
figure ttplot(EstMdl.Switch,Data=gUNRATE(idxEst)) dEst = dates(idxEst); xticklabels(string(dEst(xticks)))

Consider the following data-generating process (DGP) for a 2-D time-varying TAR (TVTAR) model containing an exogenous regression component.
State 1: , where and is the 2-by-2 identity matrix.
State 2: , where .
State 3: , where .
The exogenous threshold variable represents a linear time trend over the sample period. In this example, is the sampling period normalized by the sample size.
The system is in state 1 when , the system is in state 2 when , and the system is in state 3 otherwise.
Create a TVTAR model that represents the DGP.
tDGP = [0.3 0.6]; ttDGP = threshold(tDGP); % Constant vectors C1 = [1;-1]; C2 = [2;-2]; C3 = [3;-3]; % Common Autoregression coefficient AR = {[0.6 0.1; 0.4 0.2]}; % Regression coefficient vectors Beta1 = [0.2;-0.4]; Beta2 = [0.6;-1.0]; Beta3 = [0.9;-1.3]; % Innovations covariance matrices Sigma1 = 0.5*eye(2); Sigma2 = eye(2); Sigma3 = 1.5*eye(2); % VAR Submodels mdl1 = varm(Constant=C1,AR=AR,Beta=Beta1,Covariance=Sigma1); mdl2 = varm(Constant=C2,AR=AR,Beta=Beta2,Covariance=Sigma2); mdl3 = varm(Constant=C3,AR=AR,Beta=Beta3,Covariance=Sigma3); mdlDGP = [mdl1; mdl2; mdl3]; DGP = tsVAR(ttDGP,mdlDGP);
For the exogenous predictors , simulate a 2-D 1000-period path from the Gaussian distribution with mean 0 and standard deviation 10.
rng(1); % For reproducibility
numPeriods = 1000;
X = 10*randn(numPeriods,2);For the threshold variable, create a 1000-element vector of equally spaced elements from 0 to 1.
z = linspace(0,1,numPeriods)';
Simulate a 1000-period path from the DGP.
Y = simulate(DGP,numPeriods,X=X,Type="exogenous",Z=z);Create a TVTAR model template for estimation. Specify all estimable parameters as unknown by using NaNs.
t = [NaN NaN]; tt = threshold(t); mdl = varm(2,1); % Unknown contsant and AR coefficient by default mdl.Beta = NaN(2,1); % Configure exogenous regression component for estimation Mdl = tsVAR(tt,[mdl; mdl; mdl]);
Specify initial values of 0.25 and 0.7 for the regime thresholds.
t0 = [.25 .7]; tt0 = threshold(t0);
The largest lag among all models is 1. Therefore, the estimation procedure requires one presample observation to initialize the model.
Identify indices for the required presample, and identify indices for the estimation sample.
p = mdl.P; idxPre = 1:p; idxEst = (p + 1):numPeriods;
Fit the TVTAR model to the data. Specify presample responses Y0, characterize the threshold variable Type and provide its data Z, and specify the exogenous data X.
EstMdl = estimate(Mdl,tt0,Y(idxEst,:),Y0=Y(idxPre,:), ... Type="exogenous",Z=z(idxEst),X=X(idxEst,:));
Display an estimation summary separately for each state, and display the estimated threshold transitions.
summarize(EstMdl,1)
Description
2-Dimensional VAR Submodel, State 1
Submodel
Estimate StandardError TStatistic PValue
________ _____________ __________ ___________
State 1 Constant(1) 0.6284 0.1463 4.2952 1.7456e-05
State 1 Constant(2) -0.86147 0.1664 -5.1771 2.2538e-07
State 1 AR{1}(1,1) 0.64569 0.046378 13.922 4.6483e-44
State 1 AR{1}(2,1) 0.41777 0.052749 7.92 2.3752e-15
State 1 AR{1}(1,2) 0.11447 0.029747 3.8481 0.00011901
State 1 AR{1}(2,2) 0.18968 0.033833 5.6064 2.0657e-08
State 1 Beta(1,1) 0.12661 0.01005 12.598 2.1562e-36
State 1 Beta(2,1) -0.28306 0.01143 -24.765 2.1435e-135
summarize(EstMdl,2)
Description
2-Dimensional VAR Submodel, State 2
Submodel
Estimate StandardError TStatistic PValue
________ _____________ __________ __________
State 2 Constant(1) 2.0016 0.20741 9.6503 4.9029e-22
State 2 Constant(2) -1.919 0.2359 -8.1345 4.1377e-16
State 2 AR{1}(1,1) 0.59692 0.033401 17.871 1.9848e-71
State 2 AR{1}(2,1) 0.37274 0.03799 9.8117 1.0027e-22
State 2 AR{1}(1,2) 0.1173 0.023148 5.0674 4.0337e-07
State 2 AR{1}(2,2) 0.18002 0.026327 6.8376 8.0532e-12
State 2 Beta(1,1) 0.6689 0.014264 46.896 0
State 2 Beta(2,1) -1.122 0.016223 -69.16 0
summarize(EstMdl,3)
Description
2-Dimensional VAR Submodel, State 3
Submodel
Estimate StandardError TStatistic PValue
________ _____________ __________ ___________
State 3 Constant(1) 3.1135 0.10796 28.841 6.5868e-183
State 3 Constant(2) -3.135 0.12279 -25.533 8.5619e-144
State 3 AR{1}(1,1) 0.61547 0.011379 54.089 0
State 3 AR{1}(2,1) 0.40065 0.012942 30.958 1.9801e-210
State 3 AR{1}(1,2) 0.10685 0.0089014 12.004 3.4042e-33
State 3 AR{1}(2,2) 0.19124 0.010124 18.889 1.3979e-79
State 3 Beta(1,1) 0.92011 0.0080742 113.96 0
State 3 Beta(2,1) -1.3378 0.0091834 -145.68 0
EstMdl.Switch
ans =
threshold with properties:
Type: 'discrete'
Levels: [0.3096 0.5887]
Rates: []
StateNames: ["1" "2" "3"]
NumStates: 3
Input Arguments
Partially specified threshold-switching dynamic regression model used to indicate
constrained and estimable model parameters, specified as a tsVAR model
object returned by tsVAR. Properties of
Mdl describe the model structure and specify the parameters.
estimate treats specified parameters as equality constraints
during estimation.
estimate fits unspecified (NaN-valued)
parameters to the data Y.
Because estimate computes innovations covariances after
estimation, you cannot constrain them. If Mdl.Covariance is nonempty
(see tsVAR),
estimate provides an estimate in
EstMdl.Covariance. Otherwise, for each
i1:Mdl.NumStates, estimate provides the
innovations covariance estimate of state iEstMdl.Submodels(.i).Covariance
Fully specified threshold transitions used to initialize the estimation procedure,
specified as a threshold object returned by threshold.
Properties of a fully specified model object do not contain NaN
values.
tt0 is a copy of Mdl.Switch with
NaN values replaced by initial values for levels
(Mdl.Switch.Levels) and rates
(Mdl.Switch.Rates). Levels (tt0.Levels) and rates
(tt0.Rates) must be within the limits set by the name-value
arguments 'MaxLevel' and 'MaxRate'.
Tip
For broad coverage of the parameter space, run the algorithm from multiple
instances of tt0. For more details, see Algorithms.
Observed response data to which estimate fits the model, specified
as a numObs-by-numSeries numeric matrix.
numObs is the sample size. numSeries is the
number of response variables (Mdl.NumSeries).
Rows correspond to observations, and the last row contains the latest observation. Columns correspond to individual response variables.
Y represents the continuation of the presample response series in
Y0.
Data Types: double
Axes on which to plot the loglikelihood for each iteration when the
'IterationPlot' name-value argument is true,
specified as an Axes object.
By default, estimate plots to the current axes
(gca).
If 'IterationPlot' is false,
estimate ignores ax.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: Type="exogenous",Z=z,IterationPlot=true specifies data
z for the exogenous threshold variable and plots the loglikelihood for
each iteration.
Type of threshold variable data, specified as a value in this table.
| Value | Description |
|---|---|
"endogenous" | The model is self-exciting with threshold variable data generated by response j, where
|
"exogenous" | The threshold variable is exogenous to the system. The name-value argument 'Z' specifies the threshold variable data and is required. |
Example: Type="exogenous",Z=z specifies the data z for the exogenous threshold variable.
Example: Type="endogenous",Index=2,Delay=4 specifies the endogenous threshold variable as y2,t−4, whose data is Y(:,2).
Data Types: char | string | cell
Presample response data, specified as a
numPreSampleObs-by-numSeries numeric
matrix.
The number of presample observations numPreSampleObs must be
sufficient to initialize the AR terms of all submodels. For models of type
"endogenous", the number of presample observations must also be
sufficient to initialize the delayed response. If numPreSampleObs
exceeds the number necessary to initialize the model, estimate
uses only the latest observations. The last row contains the latest
observations.
By default, Y0 is the initial segment of
Y, which reduces the effective sample size.
Data Types: double
Threshold variable data for models of type "exogenous",
specified as a numeric vector of length at least numObs. If the
length exceeds numobs, estimate uses only
the latest observations. The last row contains the latest observation.
Data Types: double
Threshold variable delay d in
yj,t−d,
for models of type "endogenous", specified as a positive
integer.
Example: Delay=4 specifies that the threshold variable is
y2,t−d,
where j is the value of Index
.
Data Types: double
Threshold variable index j in
yj,t−d
for models of type "endogenous", specified as a scalar in
1:Mdl.NumSeries.
estimate ignores Index for univariate
AR models.
Example: Index=2 specifies that the threshold variable is
y2,t−d,
where d is the value of Delay.
Data Types: double
Predictor data used to evaluate regression components in all submodels of
Mdl, specified as a numeric matrix or a cell vector of numeric
matrices.
To use a subset of the same predictors in each state, specify X
as a matrix with numPreds columns and at least
numObs rows. Columns correspond to distinct predictor variables.
Submodels use initial columns of the associated matrix, in order, up to the number of
submodel predictors. The number of columns in the Beta property of
Mdl.SubModels( determines the
number of exogenous variables in the regression component of submodel
j)jnumObs, then estimate uses the latest
observations.
To use different predictors in each state, specify a cell vector of such matrices
with length numStates.
By default, estimate ignores regression components in
Mdl.
Data Types: double
Maximum deviation of estimated threshold levels above or below the threshold variable data, z or yj,t−d, specified as a positive numeric scalar representing the percent of the range.
The default value 0 means that initial and estimated levels
must be within the range of the data. A value greater than 0
expands the range of the search.
Example: MaxLevel=10 expands the search for levels 10% above and
below the range of the threshold variable data.
Data Types: double
Maximum estimated threshold transition rates, specified as a positive numeric
scalar or vector with length equal to the number of rates in
Mdl.Switch.Rates.
For a scalar, all estimated rates are bounded by MaxRate. For a
vector, the estimate of
Mdl.Switch.Rate( is bounded by
j)MaxRate(.j)
estimate estimates discrete transition levels as logistic
transitions at MaxRate.
The default value is 10 for each rate.
Example: MaxLevel=3 bounds all estimated rates in
Mdl.Switch.Rates by 3.
Example: MaxLevel=[5 10] bounds
Mdl.Switch.Rates(1) by 5 and bounds
Mdl.Switch.Rates(2) by 10.
Data Types: double
Limit on the number of iterations of the threshold search algorithm, specified as a positive integer.
Example: MaxIterations=1000
Data Types: double
Convergence tolerance, specified as a positive numeric scalar. The search
algorithm terminates after an iteration in which the optimality tolerance on
loglikelihood objective logL changes by less than the value of
Tolerance.
Example: Tolerance=1e-4
Data Types: double
Flag indicating whether to show a plot of the loglikelihood versus iteration step at algorithm termination, specified as a value in this table.
| Value | Description |
|---|---|
true | When the algorithm terminates, estimate shows a
plot of the loglikelihood at each iteration step. |
false | estimate does not show a plot. |
Example: IterationPlot=true
Data Types: logical
Output Arguments
Estimated threshold-switching dynamic regression model, returned as a tsVAR object.
EstMdl is a copy of Mdl that has
NaN values replaced with parameter estimates.
EstMdl is fully specified.
Estimated loglikelihood of the data in Y from the conditional
least-squares problem, returned as a numeric scalar and evaluated at the optimal
parameter values in the threshold transitions EstMdl.Switch. For more
details, see Algorithms.
Handle to the iteration plot, returned as a graphics object when IterationPlot is true.
h contains a unique plot identifier, which you can use to query or modify properties of the plot.
Tips
Several factors can lead to poor estimates of model parameters. The factors include:
Threshold data does not cross levels or sufficiently sample submodels.
Mdlcontains more estimable parameters than the sample size supports.High-rate transitions are indistinguishable.
Self-exciting autoregressive models have multiple sources of endogenous dynamics.
To improve estimates, perform these actions:
Control the parameter search by experimenting with the
'MaxLevel'and'MaxRate'name-value arguments.Consider a parsimonious model with initial levels within the range of threshold variable data.
Constrain specific parameters to potentially improve performance.
To estimate the delay d in a self-exciting model, compare the loglikelihood
logLwith different specifications for the'Delay'name-value argument. In practice, usually d is limited to a range of reasonable values.You can estimate a simple time-varying STAR (TVSTAR) model by specifying exogenous threshold data z = t, which is a linear time trend over the sample period [3].
Algorithms
estimatesearches over levels and rates forEstMdl.Switchwhile solving a conditional least-squares problem for submodel parameters, maximizing the data likelihood, as described in [4].logLis conditional on the optimal parameter values inEstMdl.Switch.Models with smooth transitions (STAR models) represent the response as a weighted mixture of conditional means from all submodels ([4], Eqn. 3.6).
estimatedetermines the weights by the value of the threshold variable, z or yj,t−d, relative to threshold levels.estimatetreats models with discrete transitions (TAR models) as logistic STAR models with transition rates set to'MaxRate'in order to disambiguate search levels that fall between threshold variable data.estimatehandles two types of equality constraints.estimatecomputes innovations variances and covariances after estimation. Therefore, you cannot constrain them.
References
[1] Chan, Kung-Sik, and Howell Tong. “On Estimating Thresholds in Autoregressive Models.” Journal of Time Series Analysis 7 (May 1986): 179–90. https://doi.org/10.1111/j.1467-9892.1986.tb00501.x.
[2] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[3] Teräsvirta, Tima. "Modelling Economic Relationships with Smooth Transition Regressions." In A. Ullahand and D.E.A. Giles (eds.), Handbook of Applied Economic Statistics, 507–552. New York: Marcel Dekker, 1998.
[4] van Dijk, Dick. Smooth Transition Models: Extensions and Outlier Robust Inference. Rotterdam, Netherlands: Tinbergen Institute Research Series, 1999.
Version History
Introduced in R2021b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)