Rounding Mode: Simplest
The simplest rounding mode attempts to reduce or eliminate the need for extra rounding code in your generated code using a combination of techniques. In nearly all cases, the simplest rounding mode produces the most efficient generated code.
For a very specialized case of division that meets three specific criteria, round to floor might be more efficient. These three criteria are:
Fixed-point/integer signed division
Denominator is an invariant constant
Denominator is an exact power of two
For this case, set the rounding mode to floor and the Model Configuration Parameters > Hardware Implementation > Production Hardware > Signed integer division rounds to parameter to describe the rounding behavior of your production target.
Optimize Rounding for Casts
The Data Type Conversion block casts a signal with one data type to another data type. When the block casts the signal to a data type with a shorter word length than the original data type, precision is lost and rounding occurs. The simplest rounding mode automatically chooses the best rounding for these cases based on the following rules:
When casting from one integer or fixed-point data type to another, the simplest mode rounds toward floor.
When casting from a floating-point data type to an integer or fixed-point data type, the simplest mode rounds toward zero.
Optimize Rounding for High-Level Arithmetic Operations
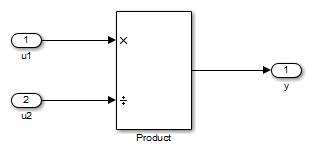
The simplest rounding mode chooses the best rounding for each high-level arithmetic operation. For example, consider the operation y = u1 × u2 / u3 implemented using a Product block:

As stated in the C standard, the most efficient rounding mode for multiplication operations is always floor. However, the C standard does not specify the rounding mode for division in cases where at least one of the operands is negative. Therefore, the most efficient rounding mode for a divide operation with signed data types can be floor or zero, depending on your production target.
The simplest rounding mode:
Rounds to floor for all non-division operations.
Rounds to zero or floor for division, depending on the setting of the Model Configuration Parameters > Hardware Implementation > Production Hardware > Signed integer division rounds to parameter.
To get the most efficient code, you must set the Signed integer division
rounds to parameter to specify whether your production target rounds
to zero or to floor for integer division. Most production targets round to zero for
integer division operations. Note that Simplest rounding
enables “mixed-mode” rounding for such cases, as it rounds to floor
for multiplication and to zero for division.
If the Signed integer division rounds to parameter is set to
Undefined, the simplest rounding mode might not be
able to produce the most efficient code. The simplest mode rounds to zero for
division for this case, but it cannot rely on your production target to perform the
rounding, because the parameter is Undefined. Therefore,
you need additional rounding code to ensure rounding to zero behavior.
Note
For signed fixed-point division where the denominator is an invariant constant power of 2, the simplest rounding mode does not generate the most efficient code. In this case, set the rounding mode to floor.
Optimize Rounding for Intermediate Arithmetic Operations
For fixed-point arithmetic with nonzero slope and bias, the simplest rounding mode also chooses the best rounding for each intermediate arithmetic operation. For example, consider the operation y = u1 / u2 implemented using a Product block, where u1 and u2 are fixed-point quantities:
As discussed in Data Types and Scaling in Digital Hardware, each fixed-point quantity is calculated using its slope, bias, and stored integer. In this example, the high-level divide operation specified by the block results in intermediate addition and multiplication operations:
The simplest rounding mode performs the best rounding for each of these operations, high-level and intermediate, to produce the most efficient code. The rules used to select the appropriate rounding for intermediate arithmetic operations are the same as those described in Optimize Rounding for High-Level Arithmetic Operations. Again, this enables mixed-mode rounding, with the most common case being round toward floor used for additions, subtractions, and multiplies, and round toward zero used for divides.
Remember that generating the most efficient code using the simplest rounding mode requires you to set the Model Configuration Parameters > Hardware Implementation > Production Hardware > Signed integer division rounds to parameter to describe the rounding behavior of your production target.
Note
For signed fixed-point division where the denominator is an invariant constant power of 2, the simplest rounding mode does not generate the most efficient code. In this case, set the rounding mode to floor.