initialCondition
Initial condition representation for linear time-invariant systems
Description
An initialCondition object encapsulates the initial-condition
information for a linear time-invariant (LTI) model. The object generalizes the numeric vector
representation of the initial states of a state-space model so that the information applies to
linear models of any form—transfer functions, polynomial models, or state-space models.
You can estimate and retrieve initial conditions when you identify a linear model using
commands such as tfest or compare model response to measured
input/output data using compare. The software estimates the initial
condition value by minimizing the simulation or prediction error against the measured output
data. You can then apply those initial conditions in a subsequent simulation, using commands
such as sim or predict, to confirm model performance with respect to the same measurement data.
Use the initialCondition command to create an
initialCondition object from a state-space model specification or from any
LTI model of a free response.
The initialCondition object can also be seen as a representation of the
free response of a linear model. The simulation functions use this information to compute the
model response in the following manner:
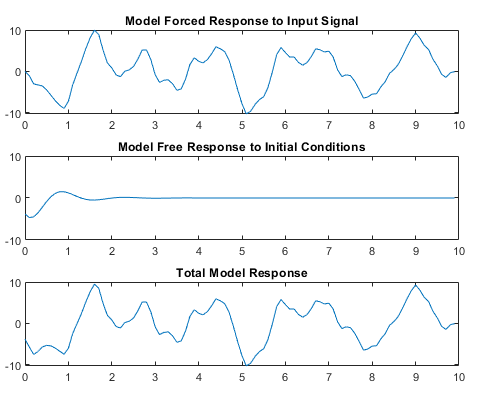
Compute the forced response of the model to the input signal. The forced response is the standard simulation output when there are no specified initial conditions.
Compute the impulse response of the model and scale the result to generate the free response of the model to the specified initial conditions.
Add the forced response and the free response together to form the total system response.
The figure illustrates this process.
For continuous systems (Ts = 0), the free response G(s) for the initial state vector x0 is
Here, C is equivalent to the state-space measurement matrix C and A is equivalent to the state-space state matrix A.
For discrete systems (Ts >0), the free response G(z) is
The initialCondition object represents the free response in state-space
form. The object is a structure with properties containing the state-space
A and C matrices and the initial state vector
x0. For idtf and
idpoly models, using an initialCondition object is the
only way to represent and use initial conditions for simulation. For idss
models, you can use either an initialCondition object or a numeric initial
state vector. When you obtain initial conditions ic for multiexperiment
data, ic is an object array, with one initialCondition
object for each experiment.
Creation
You can obtain an initialCondition object in one of four ways.
Model estimation — Specify that the estimation function return the estimated initial condition that corresponds to the estimation input/output data. For example, you can use the following command to obtain the estimated initial condition
icfor a transfer function modelsysthat is estimated with input/output dataz.For an example, see Obtain Estimated Initial Conditions.[sys,ic] = tfest(z,2,1)
Model-to-data comparison using any input/output data — Specify that
comparereturn the estimated initial condition that the function estimates internally to support thefitassessment. For example, you can use the following command to obtain the initial conditionicfor the linear modelsyswhen determining the fit against input/output dataz.ypis the simulated or predicted model output.For an example, see Obtain Initial Conditions for New Data.[yp,fit,ic] = compare(z,sys)
Direct construction — Use the
initialConditioncommand to encapsulate the state-space form of a free-response model in aninitialConditionobject.For an example, see Construct initialCondition Object from State-Space Model.ic = initialCondition(A,X0,C,Ts)
Free-response model conversion — Use the
initialConditioncommand to convert an LTI free-response model into aninitialConditionobject.ic = initialCondition(G)
For an example, see Convert Free-Response Model to initialCondition Object.
For information on functions you can use to extract information from or transform
initialCondition objects, see Object Functions.
Description
ic = initialCondition(A,X0,C,Ts)initialCondition object that represents the free response to an initial
condition, expressed in state-space form, of an LTI model.
ic stores this model in the form of properties.
A and C correspond to a state-space realization of the model, X0 to the initial state vector x0,
and Ts to the sample time. You can use ic to specify
initial conditions when simulating any type of LTI system.
Input Arguments
Properties
Object Functions
Functions applicable to initialCondition objects are those that can
return, use, or convert the objects.
| Initial Condition (IC) Role | LTI Function Type | Syntax Example | Example Links |
|---|---|---|---|
| Return estimated IC objects | All estimation functions, compare | [sys,ic] = tfest(data,2,1) | Obtain Estimated Initial Conditions |
| Use IC objects for model response | Option sets for model response functions | opt = simOptions('InitialCondition',ic) | Apply Initial Conditions in Simulation |
| Convert IC objects into Dynamic System Models (DSMs) | DSM object functions | g = idtf(ic) | Visualize Free Response to Initial Condition |
| Analyze models converted from IC objects | DSM analysis functions | y_g = impulse(g) | Visualize Free Response to Initial Condition |
Examples
Version History
Introduced in R2020b












