eqaconicstd
Albers Equal-Area Conic Projection — Standard
Classification
Conic
Identifier
eqaconicstd
Graticule
Meridians: Equally spaced straight lines converging to a common point, usually beyond the pole. The angles between the meridians are less than the true angles.
Parallels: Unequally spaced concentric circular arcs centered on the point of convergence. Spacing of parallels decreases away from the central latitudes.
Poles: Normally circular arcs, enclosing the same angle as the displayed parallels.
Symmetry: About any meridian.
Features
This function implements the Albers Equal Area Conic projection
directly on a reference ellipsoid, consistent with the industry-standard
definition of this projection. See eqaconic for
an alternative implementation based on rotating the authalic sphere.
This is an equal area projection. Scale is true along the one or two selected standard parallels. Scale is constant along any parallel; the scale factor of a meridian at any given point is the reciprocal of that along the parallel to preserve equal area. The projection is free of distortion along the standard parallels. Distortion is constant along any other parallel. This projection is neither conformal nor equidistant.
Parallels
The cone of projection has interesting limiting forms. If a pole is selected as a single standard parallel, the cone is a plane and a Lambert Azimuthal Equal-Area projection results. If two parallels are chosen, not symmetric about the Equator, then a Lambert Equal-Area Conic projection results. If a pole is selected as one of the standard parallels, then the projected pole is a point, otherwise the projected pole is an arc. If the Equator is chosen as a single parallel, the cone becomes a cylinder and a Lambert Equal-Area Cylindrical projection is the result. Finally, if two parallels equidistant from the Equator are chosen as the standard parallels, a Behrmann or other equal-area cylindrical projection is the result. Suggested parallels for maps of the conterminous U.S. are [29.5 45.5]. The default parallels are [15 75].
Remarks
This projection was presented by Heinrich Christian Albers in 1805 and it is also known as a Conical Orthomorphic projection. The cone of projection has interesting limiting forms. If a pole is selected as a single standard parallel, the cone is a plane, and a Lambert Equal Area Conic projection is the result. If the Equator is chosen as a single parallel, the cone becomes a cylinder and a Lambert Cylindrical Equal Area Projection is the result. Finally, if two parallels equidistant from the Equator are chosen as the standard parallels, a Behrmann or other cylindrical equal area projection is the result.
Mapping Toolbox™ uses a different implementation of the standard Albers equal-area conic projection for displaying coordinates on
axesm-based maps than for projecting coordinates using theprojfwdorprojinvfunction. These implementations may produce differing results.
Example
landareas = shaperead('landareas.shp','UseGeoCoords',true);
axesm ('eqaconicstd', 'Frame', 'on', 'Grid', 'on');
geoshow(landareas,'FaceColor',[1 1 .5],'EdgeColor',[.6 .6 .6]);
tissot;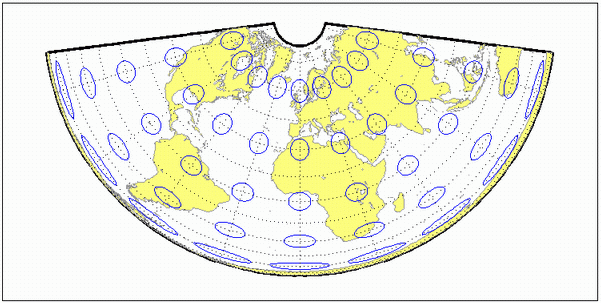
See also
Version History
Introduced before R2006a