conv2
2-D convolution
Description
C = conv2(A,B)A and B.
If
Ais a matrix andBis a row vector (orAis a row vector andBis a matrix), thenCis the convolution of each row of the matrix with the vector.If
Ais a matrix andBis a column vector (orAis a column vector andBis a matrix), thenCis the convolution of each column of the matrix with the vector.
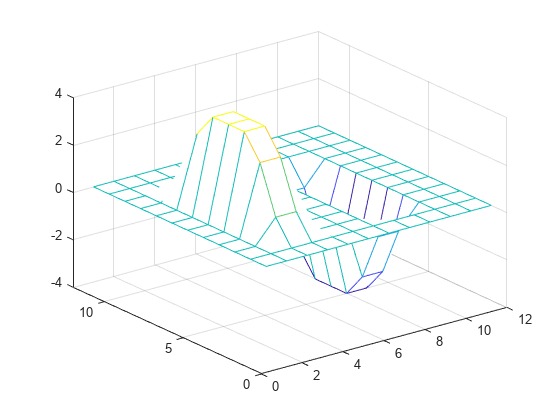
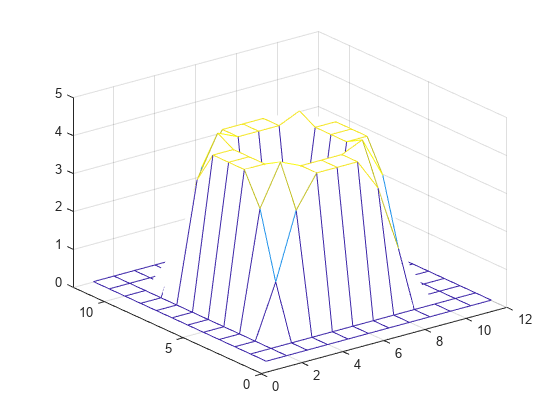
Examples
Input Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced before R2006a