deconv
Least-squares deconvolution and polynomial division
Description
Polynomial Long Division
[ deconvolves a
vector x,r] =
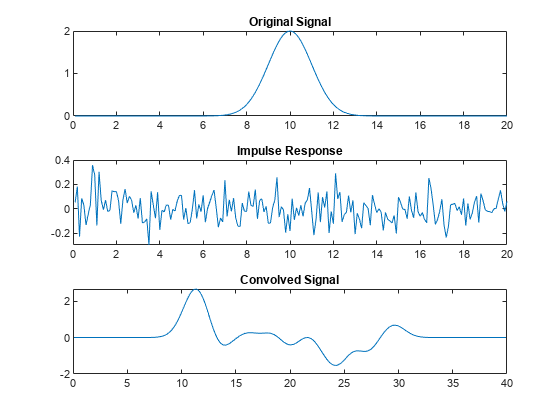
deconv(y,h)h out of a vector y using
polynomial long division, and returns the quotient x and
remainder r such that y = conv(x,h) + r.
If y and h are vectors of polynomial
coefficients, then deconvolving them is equivalent to dividing the polynomial
represented by y by the polynomial represented by
h.
Least-Squares Deconvolution
Since R2023b
[
specifies the subsections of the convolved signal x,r] =
deconv(y,h,shape)y, where
y = conv(x,h,shape) + r.
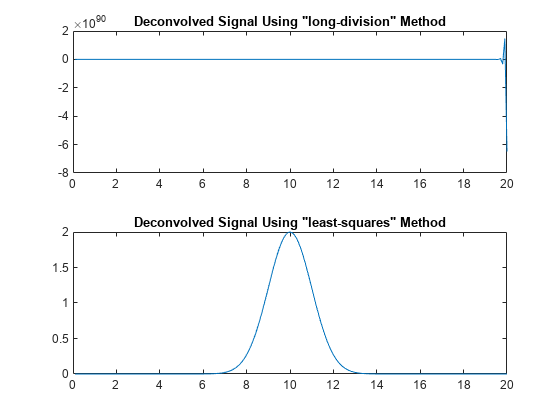
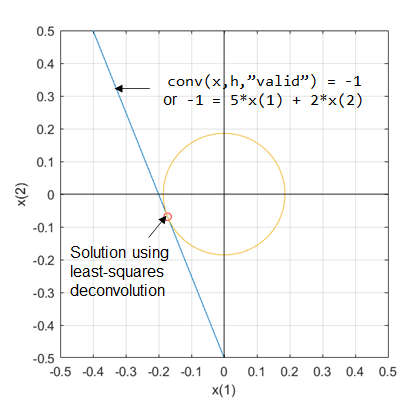
If you use the least-squares deconvolution method
(Method="least-squares"), then you can specify
shape as "full",
"same", or "valid". Otherwise, if you
use the default long-division deconvolution method
(Method="long-division"), then shape
must be "full".
[ specifies options
using one or more name-value arguments in addition to any of the input argument
combinations in previous syntaxes.x,r] =
deconv(___,Name=Value)
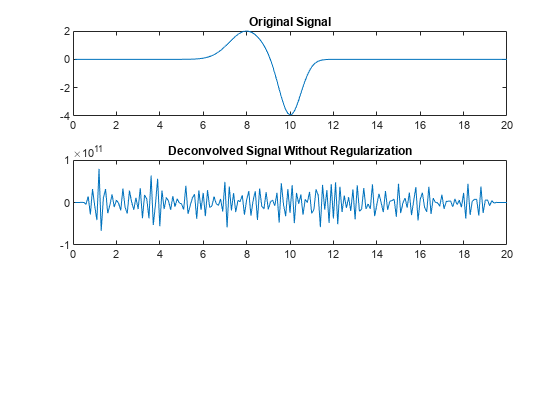
You can specify the deconvolution method using
deconv(__,Method=algorithm), wherealgorithmcan be"long-division"or"least-squares".You can also specify the Tikhonov regularization factor to the least-squares solution of the deconvolution method using
deconv(__,RegularizationFactor=alpha).
Examples
Input Arguments
Name-Value Arguments
Output Arguments
References
[1] Nagy, James G. “Fast Inverse QR Factorization for Toeplitz Matrices.” SIAM Journal on Scientific Computing 14, no. 5 (September 1993): 1174–93. https://doi.org/10.1137/0914070.