isisomorphic
Determine whether two graphs are isomorphic
Description
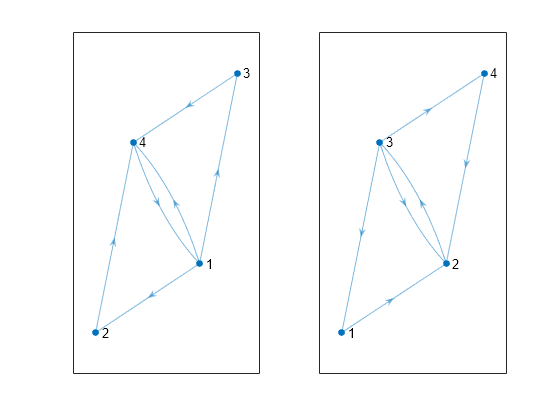
tf = isisomorphic( returns logical
G1,G2)1 (true) if a graph isomorphism exists
between graphs G1 and G2; otherwise, it
returns logical 0 (false).
tf = isisomorphic(
specifies additional options with one or more name-value pair arguments. For
example, you can specify G1,G2,Name,Value)'NodeVariables' and a list of node
variables to indicate that the isomorphism must preserve these variables to be
valid.
Examples
Input Arguments
Name-Value Arguments
More About
Extended Capabilities
Version History
Introduced in R2016b