isomorphism
Compute isomorphism between two graphs
Description
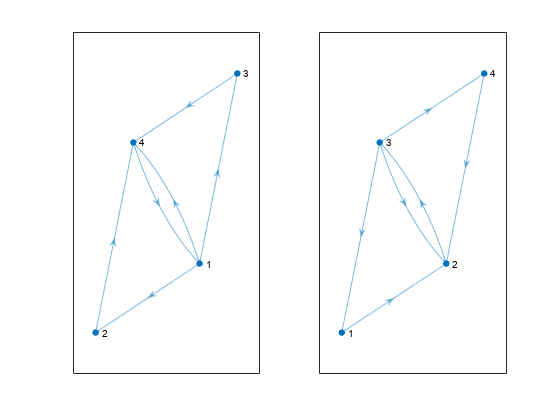
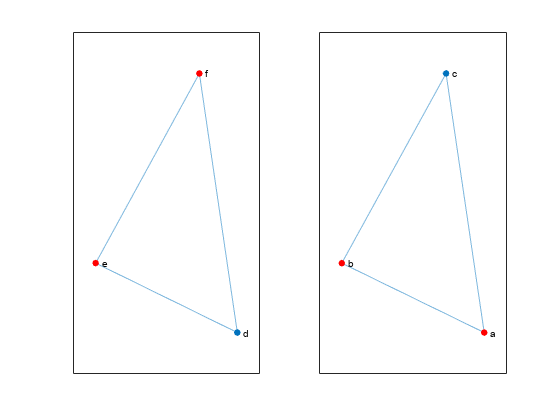
P = isomorphism(G1,G2)G1 and G2,
if one exists. If no isomorphism exists, then P is an empty
array.
P = isomorphism(___,Name,Value)'NodeVariables' and a list of node
variables to indicate that the isomorphism must preserve these variables to be
valid.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced in R2016b