interpft
1-D interpolation (FFT method)
Description
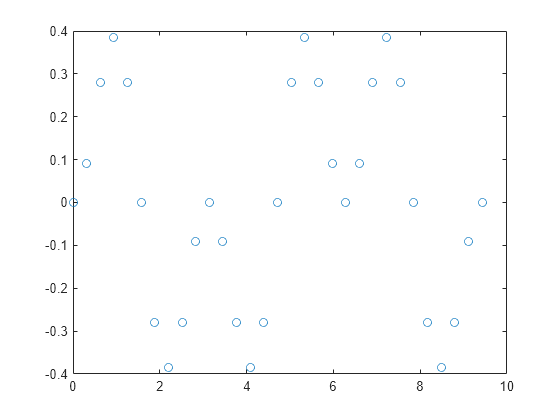
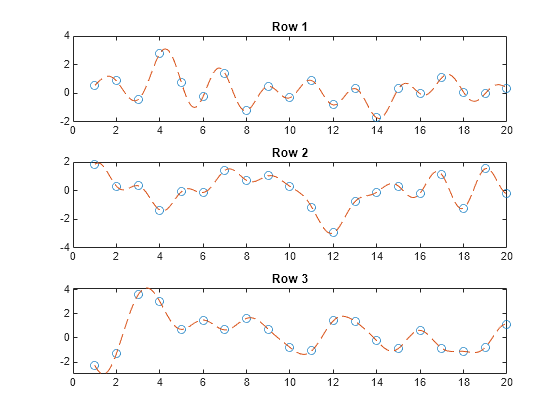
Examples
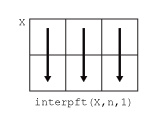
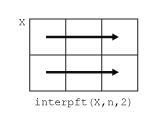
Input Arguments
Output Arguments
Algorithms
The interpft function uses the FFT method. The original vector
x is transformed to the Fourier domain using
fft, and then it is transformed back with more points.
Extended Capabilities
Version History
Introduced before R2006a