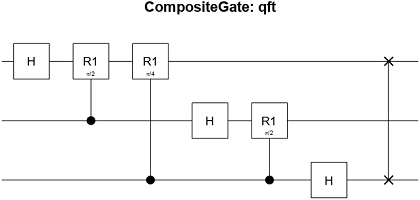
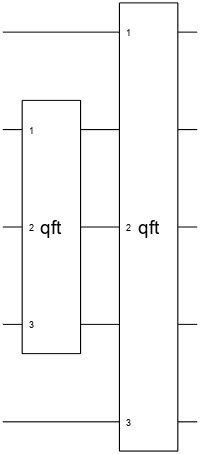
qftGate
Installation Required: This functionality requires MATLAB Support Package for Quantum Computing.
Description
cg = qftGate(targetQubits)quantum.gate.CompositeGate object with a Name property of
"qft".
Examples
Input Arguments
More About
References
[1] Nielsen, Michael A., and Isaac L. Chuang. Quantum Computation and Quantum Information. 10th anniversary ed, Cambridge; New York: Cambridge University Press, 2010.
Version History
Introduced in R2023a