rlContinuousDeterministicTransitionFunction
Deterministic transition function approximator object for neural network-based environment
Since R2022a
Description
When creating a neural network-based environment using rlNeuralNetworkEnvironment, you can specify deterministic transition function
approximators using rlContinuousDeterministicTransitionFunction
objects.
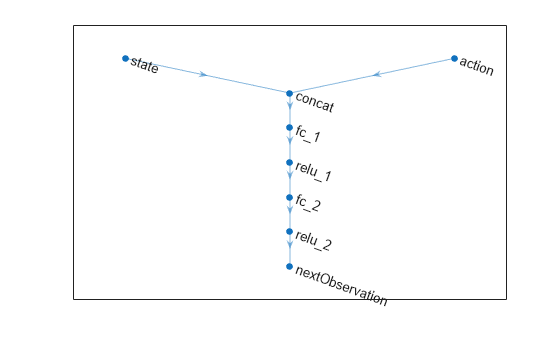
A transition function approximator object uses a deep neural network to predict the next observations based on the current observations and actions.
To specify stochastic transition function approximators, use rlContinuousGaussianTransitionFunction objects.
Creation
Syntax
Description
tsnFcnAppx = rlContinuousDeterministicTransitionFunction(net,observationInfo,actionInfo,Name=Value)net and sets the ObservationInfo and
ActionInfo properties.
When creating a deterministic transition function approximator you must specify the
names of the deep neural network inputs and outputs using the
ObservationInputNames, ActionInputNames, and
NextObservationOutputNames name-value pair arguments.
You can also specify the PredictDiff and
UseDevice properties using optional name-value pair arguments. For
example, to use a GPU for prediction, specify UseDevice="gpu".
Input Arguments
Name-Value Arguments
Properties
Object Functions
rlNeuralNetworkEnvironment | Environment model with deep neural network transition models |
Examples
Version History
Introduced in R2022a