goertzel

Discrete-Time Fourier transform with second-order Goertzel algorithm

Syntax

dft = goertzel(data)

dft = goertzel(data,findx)

dft = goertzel(data,findx,dim)

Description

dft = goertzel(data) returns the discrete-time Fourier transform (DTFT) of the input array data using a second-order Goertzel algorithm. If data has more than one dimension, then goertzel operates along the first array dimension with size greater than 1. For more information, see Algorithms.

dft = goertzel(data,findx) returns the DTFT for the frequency indices specified in findx as a vector of integers or nonintegers.

dft = goertzel(data,findx,dim) computes the DTFT along dimension dim. To input a dimension and use the default value of findx, specify the second argument as empty, [].

Examples

Discrete-Time Fourier Transform with Goertzel Algorithm

Compare the output of goertzel to the result of a direct-form-II implementation of the Goertzel algorithm.

Define a chirp signal xn sampled at 50 Hz for 10 seconds and embedded in white Gaussian noise. The chirp's frequency increases linearly from 15 Hz to 20 Hz during the measurement.

fs = 50;
t = 0:1/fs:10-1/fs;
N = length(t);
xn = chirp(t,15,t(end),20) + randn(1,N)/100;

Define a frequency from which to compute its discrete Fourier transform (DTFT) that is not an integer multiple of fs/N.

f0 = 17.36;
k = N*f0/fs;

Compute the DTFT of xn using the direct-form-II implementation of the second-order Goertzel algorithm.

ykn = filter([1 -exp(-2j*pi*k/N)],[1 -2*cos(2*pi*k/N) 1],[xn 0]);
Xk = exp(-2j*pi*k)*ykn(end)

Xk = 
-30.5384 -14.3396i

Compute the DTFT of xn using the goertzel function. When calling goertzel, keep in mind that MATLAB® vectors run from 1 to N instead of from 0 to N – 1.

dft = goertzel(xn,k+1)

dft = 
-30.5384 -14.3396i

Compare the outputs. The results agree to high precision.

df = abs(Xk-dft)

df = 
4.3634e-12

Estimate Telephone Keypad Frequencies

Estimate the frequencies of the tone generated by pressing the 1 button on a telephone keypad.

The number 1 produces a tone with frequencies 697 and 1209 Hz. Generate 205 samples of the tone with a sample rate of 8 kHz.

Fs = 8000;
N = 205;
lo = sin(2*pi*697*(0:N-1)/Fs);
hi = sin(2*pi*1209*(0:N-1)/Fs);
data = lo + hi;

Use the Goertzel algorithm to compute the discrete-time Fourier transform (DTFT) of the tone. Choose the indices corresponding to the frequencies used to generate the numbers 0 through 9.

f = [697 770 852 941 1209 1336 1477];
freq_indices = round(f/Fs*N) + 1;   
dtft_data = goertzel(data,freq_indices);

Plot the DTFT magnitude.

stem(f,abs(dtft_data))

ax = gca;
ax.XTick = f;
xlabel("Frequency (Hz)")
ylabel("DTFT Magnitude")

Centered Frequency Response of Complex Chirp

Compute the DTFT of a complex-valued chirp signal using the goertzel function and frequencies centered at 0 Hz.

Generate a signal composed of a linearly swept complex-valued chirp and a quadratic-swept real-valued chirp, sampled at 1 kHz for 10 seconds. The instantaneous frequency of the linearly swept chirp signal is from –100 Hz initially and 200 Hz at the end. The instantaneous frequency of the quadratic-swept chirp signal is from 350 Hz initially and 400 Hz at the end. The initial phase is zero.

Fs = 1e3;
t = single(0:1/Fs:10);

y = chirp(t,-100,t(end),200,"linear",0,"complex") + ...
    0.1*chirp(t,350,t(end),400,"quadratic");

Use the Goertzel algorithm to compute the DTFT of the signal. Specify frequency axes centered at 0 Hz. Plot the DTFT magnitude expressed in decibels.

F = linspace(-Fs/2,Fs/2,1001);

N = length(t);
k =  N*F/Fs;
dft = goertzel(y,k+1);

plot(F,db(dft))
xlabel("Frequency (Hz)")
ylabel("Magnitude (dB)")
grid on

Resolve Frequency Components of a Noisy Tone

Generate a noisy cosine with frequency components at 1.24 kHz, 1.26 kHz, and 10 kHz. Specify a sample rate of 32 kHz. Reset the random number generator for reproducible results.

rng default

Fs = 32e3;
t = 0:1/Fs:2.96;
x = cos(2*pi*t*10e3) + cos(2*pi*t*1.24e3) + cos(2*pi*t*1.26e3) ...
    + randn(size(t));

Generate the frequency vector. Use the Goertzel algorithm to compute the DFT. Restrict the range of frequencies to between 1.2 and 1.3 kHz.

N = (length(x)+1)/2;
f = (Fs/2)/N*(0:N-1);
indxs = find(f>1.2e3 & f<1.3e3);
X = goertzel(x,indxs);

Plot the mean squared spectrum expressed in decibels.

plot(f(indxs)/1e3,mag2db(abs(X)/length(X)))

title('Mean Squared Spectrum')
xlabel('Frequency (kHz)')
ylabel('Power (dB)')
grid

Discrete-Time Fourier Transform of N-D Array

Generate a two-channel signal sampled at 3.2 kHz for 10 seconds and embedded in white Gaussian noise. The first channel of the signal is a 124 Hz sinusoid. The second channel is a complex exponential with a frequency of 126 Hz. Reshape the signal into a three-dimensional array such that the time axis runs along the third dimension.

fs = 3.2e3;
t = 0:1/fs:10-1/fs;

x = [cos(2*pi*t*124);exp(2j*pi*t*126)] + randn(2,length(t))/100;
x = permute(x,[3 1 2]);

size(x)

ans = 1×3

           1           2       32000

Compute the discrete-time Fourier transform of the signal using the Goertzel algorithm. Restrict the range of frequencies to between 120 Hz and 130 Hz.

N = (length(x)+1)/2;
f = (fs/2)/N*(0:N-1);
indxs = find(f>=120 & f<=130);

X = goertzel(x,indxs,3);

Plot the magnitude of the discrete-time Fourier transform expressed in decibels.

plot(f(indxs),mag2db(abs(squeeze(X))))
xlabel('Frequency (Hz)')
ylabel('DTFT Magnitude (dB)')
grid

Input Arguments

data — Input array

vector | matrix | N-D array

Input array, specified as a vector, matrix, or N-D array.

Example: sin(2*pi*(0:255)/4) specifies a sinusoid as a row vector.

Example: sin(2*pi*[0.1;0.3]*(0:39))' specifies a two-channel sinusoid.

Data Types: single | double
Complex Number Support: Yes

findx — Frequency indices

vector

Frequency indices, specified as a vector. The indices can correspond to integer or noninteger multiples of f_s/N, where f_s is the sample rate and N is the signal length.

Data Types: single | double

dim — Dimension to operate along

positive integer scalar

Dimension to operate along, specified as a positive integer scalar.

Data Types: single | double

Output Arguments

dft — Discrete Fourier transform

vector | matrix | N-D array

Discrete Fourier transform, returned as a vector, matrix, or N-D array.

Tips

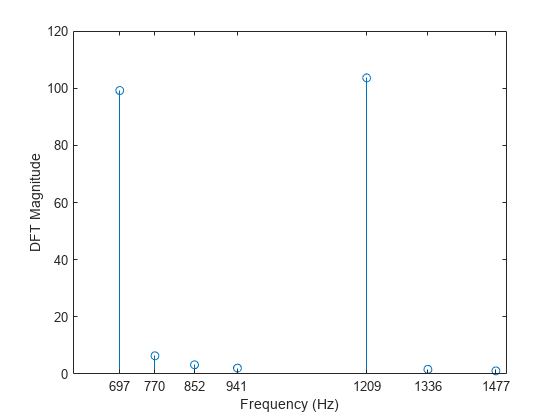
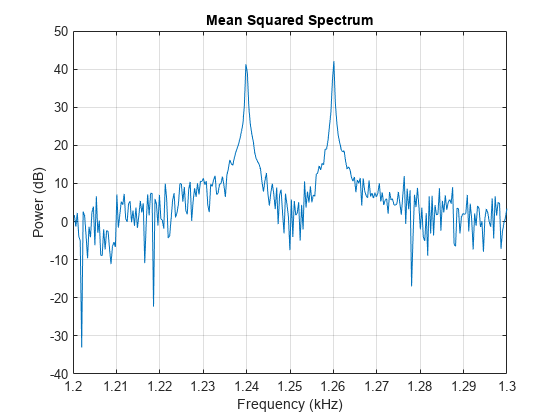
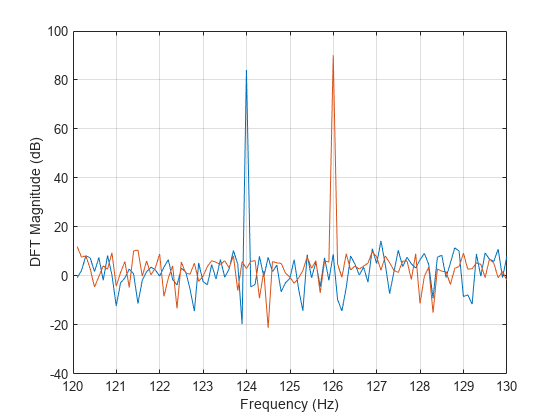
• Use the Goertzel algorithm for best efficiency when you need the DTFT at only a few frequencies.

• You can also compute the DTFT with:

  • fft — fft is more efficient than goertzel when you need to evaluate the transform at more than log₂N frequencies, where N is the length of the input signal.

  • czt — czt calculates the chirp Z-transform of an input signal on a circular or spiral contour and includes the DTFT as a special case.

Algorithms

The Goertzel algorithm implements the discrete-time Fourier transform X(k) as the convolution of an N-point input x(n), n = 0, 1, …, N – 1, with the impulse response

$$h_k(n)=e^{-j2\pi k}{e}^{j2\pi kn/N}u(n)\equiv e^{-j2\pi k}{W}_N^{-kn}u(n),$$

where u(n), the unit step sequence, is 1 for n ≥ 0 and 0 otherwise. k does not have to be an integer. At a frequency f = kf_s/N, where f_s is the sample rate, the transform has a value

$$X(k)={y_k(n)|}_{n=N},$$

where

$$y_k(n)={\displaystyle \sum _{m=0}^{N}x(m)h_k(n-m)}$$

and x(N) = 0. The Z-transform of the impulse response is

$$H_k(z)=\frac{\left(1-W_N^k{z}^{-1}\right)e^{-j2\pi k}}{1-2\cos \left(\frac{2\pi k}{N}\right)z^{-1}+z^{-2}}$$

with this direct form II implementation:

References

[1] Burrus, C. Sidney, and Thomas W. Parks. DTFT/FFT and Convolution Algorithms: Theory and Implementation. New York: John Wiley & Sons, 1985.

[2] Proakis, John G., and Dimitris G. Manolakis. Digital Signal Processing: Principles, Algorithms, and Applications. 3rd Edition. Upper Saddle River, NJ: Prentice Hall, 1996.

[3] Sysel, Petr, and Pavel Rajmic. “Goertzel Algorithm Generalized to Non-Integer Multiples of Fundamental Frequency.” EURASIP Journal on Advances in Signal Processing. Vol. 2012, Number 1, December 2012, pp. 56-1–56-8. https://doi.org/10.1186/1687-6180-2012-56.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

See Automatic dimension restriction (MATLAB Coder).

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The goertzel function supports GPU array input with these usage notes and limitations:

• For a single-channel input, executing this function on the GPU offers no performance gains. Performance on the GPU increases as the number of channels increases.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced before R2006a