mscohere
Magnitude-squared coherence
Syntax
Description
cxy = mscohere(x,y)cxy,
of the input signals, x and y.
If
xandyare both vectors, they must have the same length.If one of the signals is a matrix and the other is a vector, then the length of the vector must equal the number of rows in the matrix. The function expands the vector and returns a matrix of column-by-column magnitude-squared coherence estimates.
If
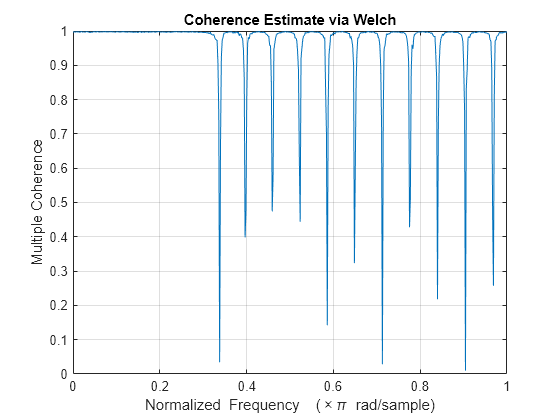
xandyare matrices with the same number of rows but different numbers of columns, thenmscoherereturns a multiple coherence matrix. The mth column ofcxycontains an estimate of the degree of correlation between all the input signals and the mth output signal. See Magnitude-Squared Coherence for more information.If
xandyare matrices of equal size, thenmscohereoperates column-wise:cxy(:,n) = mscohere(x(:,n),y(:,n)). To obtain a multiple coherence matrix, append'mimo'to the argument list.
[ returns
a vector of frequencies, cxy,f] = mscohere(___,fs)f, expressed in terms
of the sample rate, fs, at which the magnitude-squared
coherence is estimated. fs must be the sixth
numeric input to mscohere. To input a sample
rate and still use the default values of the preceding optional arguments,
specify these arguments as empty, [].
mscohere(___) with
no output arguments plots the magnitude-squared coherence estimate
in the current figure window.
Examples
Input Arguments
Output Arguments
More About
Algorithms
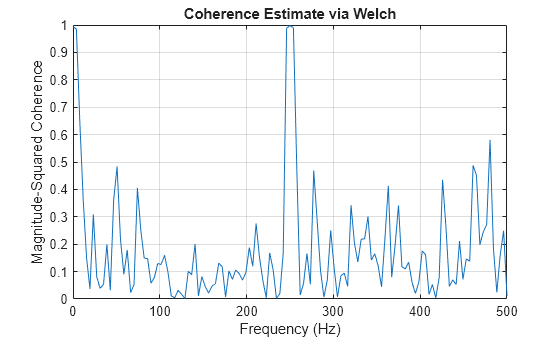
mscohere estimates the magnitude-squared
coherence function [2] using Welch’s
overlapped averaged periodogram method [3], [5].
References
[1] Gómez González, A., J. Rodríguez, X. Sagartzazu, A. Schumacher, and I. Isasa. “Multiple Coherence Method in Time Domain for the Analysis of the Transmission Paths of Noise and Vibrations with Non-Stationary Signals.” Proceedings of the 2010 International Conference of Noise and Vibration Engineering, ISMA2010-USD2010. pp. 3927–3941.
[2] Kay, Steven M. Modern Spectral Estimation. Englewood Cliffs, NJ: Prentice-Hall, 1988.
[3] Rabiner, Lawrence R., and Bernard Gold. Theory and Application of Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1975.
[4] Stoica, Petre, and Randolph Moses. Spectral Analysis of Signals. Upper Saddle River, NJ: Prentice Hall, 2005.
[5] Welch, Peter D. “The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms.” IEEE® Transactions on Audio and Electroacoustics. Vol. AU-15, 1967, pp. 70–73.