CovariateModel
Define relationship between parameters and covariates
Description
A CovariateModel object defines the relationship between
estimated parameters and covariates.
Use a CovariateModel object as an input argument to sbiofitmixed to fit a model with covariate dependencies. Before using the
CovariateModel object, set the FixedEffectValues
property to specify the initial estimates for the fixed effects.
Creation
Description
Input Arguments
Expression to define the parameter-covariate relationships, specified as a character vector, string, string vector, or cell array of character vectors.
Denote fixed effects with the prefix theta, and random effects
with the prefix eta. The expression must be in the form:
parameterName = relationship. Here is an example,
"volume = theta1 + theta2*weight". For details on additional
requirements, see the Expression property.
If a model component name or covariate name is not a valid
MATLAB® variable name, surround it by square brackets when referring to it in the
expression. For example, if the name of a species is DNA
polymerase+, write [DNA polymerase+]. If a covariate name
itself contains square brackets, you cannot use it in the expression.
This table illustrates expression formats for some common parameter-covariate relationships.
| Parameter-Covariate Relationship | Expression Format |
|---|---|
| Linear with random effect | Cl = theta1 + theta2*WEIGHT + eta1 |
| Exponential without random effect | Cl = exp(theta_Cl + theta_Cl_WT*WEIGHT) |
| Exponential, WEIGHT centered by mean, has random effect | Cl = exp(theta1 + theta2*(WEIGHT - mean(WEIGHT)) +
eta1) |
| Exponential, log(WEIGHT), which is equivalent to power model | Cl = exp(theta1 + theta2*log(WEIGHT) + eta1) |
| Exponential, dependent on WEIGHT and AGE, has random effect | Cl = exp(theta1 + theta2*WEIGHT + theta3*AGE + eta1) |
| Inverse of probit, dependent on WEIGHT and AGE, has random effect | Cl = probitinv(theta1 + theta2*WEIGHT + theta3*AGE
+ eta1) |
| Inverse of logit, dependent on WEIGHT and AGE, has random effect | Cl = logitinv(theta1 + theta2*WEIGHT + theta3*AGE
+ eta1) |
Tip
To simultaneously fit data from multiple dose levels, use a CovariateModel object
as an input argument to sbiofitmixed,
and omit the random effect (eta) from the Expression property
in the CovariateModel object.
Properties
This property is read-only.
Labels for covariates in the Expression property of the object,
returned as a cell array of character vectors.
Data Types: cell
Relationships between parameters being estimated and covariates, returned as a cell array of character vectors.
The Expression property must meet the following
requirements:
The expressions are valid MATLAB code.
Each expression is linear with a transformation.
There is exactly one expression for each parameter.
In each expression, a covariate is used in at most one term.
In each expression, there is at most one random effect (
eta)Fixed effect (
theta) and random effect (eta) names are unique within and across expressions. That is, each covariate has its own fixed effect.
For examples of some common parameter-covariate relationships, see E.
Tip
To simultaneously fit data from multiple dose levels, use a
CovariateModelobject as an input argument tosbiofitmixed, and omit the random effect (eta) from theExpressionproperty in theCovariateModelobject.Use the
getCovariateDatamethod to view the covariate data when writing equations for theExpressionproperty of aCovariateModelobject.Use the
verifymethod to check that theExpressionproperty of aCovariateModelobject meets the conditions described previously.
Data Types: cell
This property is read-only.
Descriptions of fixed effects in the Expression property of the
object, returned as a cell array of character vectors.
Each character vector describes the role of a fixed effect in the expression equation. For example, consider the following expression:
At the command line, you can create a CovariateModel object using
that
expression.
cm = CovariateModel("Cl = exp(theta1 + theta2*WEIGHT + theta3*AGE + eta1)");
cm.FixedEffectDescriptionans =
3×1 cell array
{'Cl' }
{'Cl/WEIGHT'}
{'Cl/AGE' }In this example, the description for the fixed effect theta1 is
'Cl', which indicates it is the intercept for the parameter
Cl. Also, the description for the fixed effect
theta2 is 'Cl/WEIGHT', which indicates it is the
slope of the line that defines the relationship between the parameter
Cl and the covariate WEIGHT. The description of
theta3 is 'Cl/AGE'.
Data Types: cell
This property is read-only.
Names of fixed effects in the Expression property of the
object, returned as a cell array of character vectors. The names are denoted with the
prefix theta.
Data Types: cell
Values for initial estimates of fixed effects in the Expression
property of the object, returned as a structure. Each field contains the value of the
initial estimate for each fixed effect (theta).
Tip
You must set this property before using the CovariateModel
object as input to sbionlmefit or sbionlmefitsa. Use the constructDefaultFixedEffectValues method to create a
structure of fixed-effect (theta) initial estimate values, which
are set to a default of zero. Then edit the structure to change the initial estimate
values. Then set the structure as the value of this property. For an example, see
Specify a Covariate Model.
Data Types: struct
This property is read-only.
Names of parameters in the Expression property of the object,
returned as a cell array of character vectors.
Data Types: cell
This property is read-only.
Names of random effects in the Expression property of the
object, returned as a cell array of character vectors. Each name is denoted with the
prefix eta.
Data Types: cell
Object Functions
constructDefaultFixedEffectValues | Create structure containing initial estimates fixed effects needed for fit |
verify | Check covariate model for errors |
Examples
Create an empty CovariateModel object.
covModel = CovariateModel;
Set its Expression property to define the relationships between parameters (Cl, V, and k) and covariate (w). You must use theta as a prefix for all fixed effects and eta for random effects.
covModel.Expression = ["Cl = theta1 + theta2*w + eta1","V = theta3 + eta2","k = theta4 + eta3"];
Display the names of fixed effects.
covModel.FixedEffectNames
ans = 4×1 cell
{'theta1'}
{'theta3'}
{'theta4'}
{'theta2'}
The FixedEffectDescription property displays which fixed effects correspond to which parameter. For instance, theta1 is the fixed effect for the Cl parameter, and theta2 is the fixed effect for the weight covariate that has a correlation with Cl parameter, denoted as Cl/w.
covModel.FixedEffectDescription
ans = 4×1 cell
{'Cl' }
{'V' }
{'k' }
{'Cl/w'}
Specify initial estimates for the fixed effects. Create a default structure containing initial estimates using the constructDefaultFixedEffectValues function.
initialEstimates = constructDefaultFixedEffectValues(covModel)
initialEstimates = struct with fields:
theta1: 0
theta3: 0
theta4: 0
theta2: 0
Update the initial estimate value of each fixed effects.
initialEstimates.theta1 = 1.20; initialEstimates.theta2 = 0.30; initialEstimates.theta3 = 0.90; initialEstimates.theta4 = 0.10;
Update the FixedEffectValues property to use the updated initial estimates.
covModel.FixedEffectValues = initialEstimates;
Check the covariate model for errors.
verify(covModel)
Estimate nonlinear mixed-effects parameters using clinical pharmacokinetic data collected from 59 infants. Evaluate the fitted model given new data or dosing information.
Load Data
This example uses data collected on 59 preterm infants given phenobarbital during the first 16 days after birth [1]. ds is a table containing the concentration-time profile data and covariate information for each infant (or group).
load pheno.mat ds
Convert to groupedData
Convert the data to the groupedData format for parameter estimation.
data = groupedData(ds);
Display the first few rows of data.
data(1:5,:)
ans =
5×6 groupedData
ID TIME DOSE WEIGHT APGAR CONC
__ ____ ____ ______ _____ ____
1 0 25 1.4 7 NaN
1 2 NaN 1.4 7 17.3
1 12.5 3.5 1.4 7 NaN
1 24.5 3.5 1.4 7 NaN
1 37 3.5 1.4 7 NaN
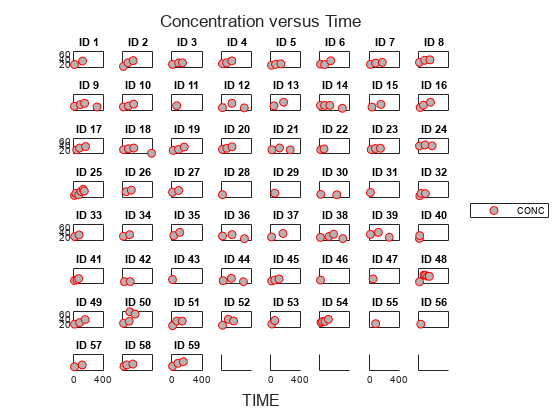
Visualize Data
Display the data in a trellis plot.
t = sbiotrellis(data, 'ID', 'TIME', 'CONC', 'marker', 'o',... 'markerfacecolor', [.7 .7 .7], 'markeredgecolor', 'r', ... 'linestyle', 'none'); t.plottitle = 'Concentration versus Time';
Create a One-Compartment PK Model
Create a simple one-compartment PK model, with bolus dose administration and linear clearance elimination, to fit the data.
pkmd = PKModelDesign; addCompartment(pkmd,'Central','DosingType','Bolus',... 'EliminationType','linear-clearance',... 'HasResponseVariable',true,'HasLag',false); onecomp = pkmd.construct;
Map model species to response data.
responseMap = 'Drug_Central = CONC';Define Estimated Parameters
The parameters to estimate in this model are the volume of the central compartment (Central) and the clearance rate (Cl_Central). sbiofitmixed calculates fixed and random effects for each parameter. The underlying algorithm computes normally distributed random effects, which might violate constraints for biological parameters that are always positive, such as volume and clearance. Therefore, specify a transform for the estimated parameters so that the transformed parameters follow a normal distribution. The resulting model is
and
where , , and are the fixed effects, random effects, and estimated parameter values respectively, calculated for each infant (group) . Some arbitrary initial estimates for V (volume of central compartment) and Cl (clearance rate) are used here in the absence of better empirical data.
estimatedParams = estimatedInfo({'log(Central)','log(Cl_Central)'},'InitialValue',[1 1]);Define Dosing
All infants were given the drug, represented by the Drug_Central species, where the dosing schedule varies among infants. The amount of drug is listed in the data variable DOSE. You can automatically generate dose objects from the data and use them during fitting. In this example, Drug_Central is the target species that receives the dose.
sampleDose = sbiodose('sample','TargetName','Drug_Central'); doses = createDoses(data,'DOSE','',sampleDose);
Fit the Model
Use sbiofitmixed to fit the one-compartment model to the data.
nlmeResults = sbiofitmixed(onecomp,data,responseMap,estimatedParams,doses,'nlmefit');Visualize Results
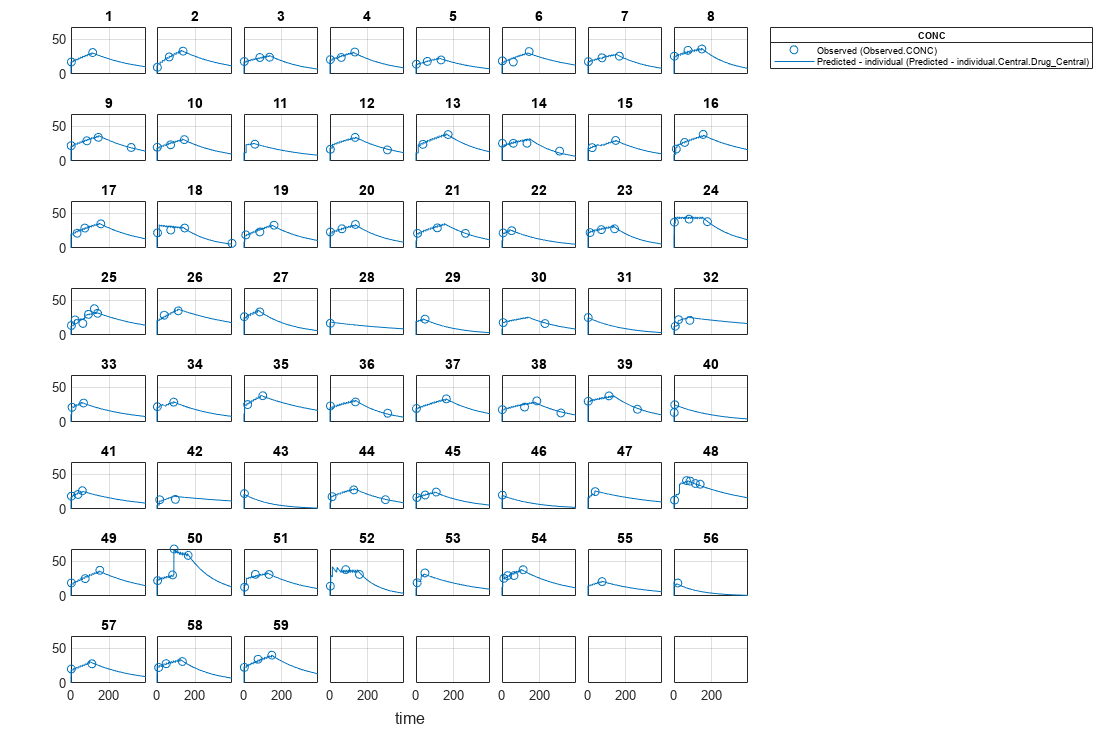
Visualize the fitted results using individual-specific parameter estimates.
plot(nlmeResults,'ParameterType','individual');
Use New Dosing Data to Simulate the Fitted Model
Suppose you want to predict how infants 1 and 2 would have responded under different dosing amounts. You can predict their responses as follows.
Create new dose objects with new dose amounts.
dose1 = doses(1); dose1.Amount = dose1.Amount*2; dose2 = doses(2); dose2.Amount = dose2.Amount*1.5;
Use the predict function to evaluate the fitted model using the new dosing data. If you want response predictions at particular times, provide the new output time vector. Use the 'ParameterType' option to specify individual or population parameters to use. By default, predict uses the population parameters when you specify output times.
timeVec = [0:25:400]; newResults = predict(nlmeResults,timeVec,[dose1;dose2],'ParameterType','population');
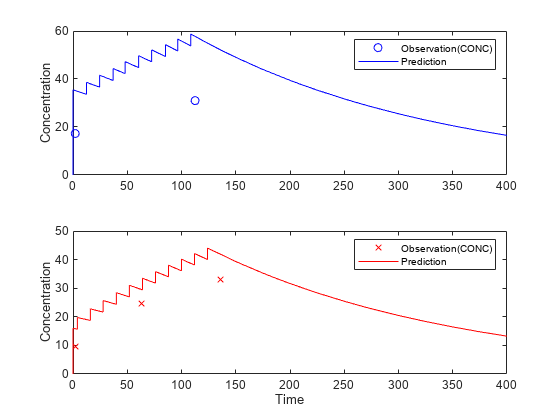
Visualize the predicted responses while overlapping the experimental data for infants 1 and 2.
figure; subplot(2,1,1) plot(data.TIME(data.ID == 1),data.CONC(data.ID == 1),'bo') hold on plot(newResults(1).Time,newResults(1).Data,'b') hold off ylabel('Concentration') legend('Observation(CONC)','Prediction') subplot(2,1,2) plot(data.TIME(data.ID == 2),data.CONC(data.ID == 2),'rx') hold on plot(newResults(2).Time,newResults(2).Data,'r') hold off legend('Observation(CONC)','Prediction') ylabel('Concentration') xlabel('Time')
Create a Covariate Model for the Covariate Dependencies
Suppose there is a correlation between volume and weight, and possibly volume and APGAR score. Consider the effect of weight by modeling two of these covariate dependencies: the volume of central (Central) and the clearance rate (Cl_Central) vary with weight. The model becomes
and
Use the CovariateModel object to define the covariate dependencies. For details, see Specify a Covariate Model.
covModel = CovariateModel;
covModel.Expression = ({'Central = exp(theta1 + theta2*WEIGHT + eta1)',...
'Cl_Central = exp(theta3 + theta4*WEIGHT + eta2)'});Use constructDefaultInitialEstimate to create an initialEstimates struct.
initialEstimates = covModel.constructDefaultFixedEffectValues;
Use the FixedEffectNames property to display the thetas (fixed effects) defined in the model.
covModel.FixedEffectNames
ans = 4×1 cell
{'theta1'}
{'theta3'}
{'theta2'}
{'theta4'}
Use the FixedEffectDescription property to show the descriptions of corresponding fixed effects (thetas) used in the covariate expression. For example, theta2 is the fixed effect for the weight covariate that correlates with the volume (Central), denoted as 'Central/WEIGHT'.
disp('Fixed Effects Description:');Fixed Effects Description:
disp(covModel.FixedEffectDescription);
{'Central' }
{'Cl_Central' }
{'Central/WEIGHT' }
{'Cl_Central/WEIGHT'}
Set the initial guesses for the fixed-effect parameter values for Central and Cl_Central using the values estimated from fitting the base model.
initialEstimates.theta1 = nlmeResults.FixedEffects.Estimate(1); initialEstimates.theta3 = nlmeResults.FixedEffects.Estimate(2); covModel.FixedEffectValues = initialEstimates;
Fit the Model
nlmeResults_cov = sbiofitmixed(onecomp,data,responseMap,covModel,doses,'nlmefit');Display Fitted Parameters and Covariances
disp('Estimated Fixed Effects:');Estimated Fixed Effects:
disp(nlmeResults_cov.FixedEffects);
Name Description Estimate StandardError
__________ _____________________ ________ _____________
{'theta1'} {'Central' } -0.45664 0.078933
{'theta3'} {'Cl_Central' } -5.9519 0.1177
{'theta2'} {'Central/WEIGHT' } 0.52948 0.047342
{'theta4'} {'Cl_Central/WEIGHT'} 0.61954 0.071386
disp('Estimated Covariance Matrix:');Estimated Covariance Matrix:
disp(nlmeResults_cov.RandomEffectCovarianceMatrix);
eta1 eta2
________ ________
eta1 0.046503 0
eta2 0 0.041609
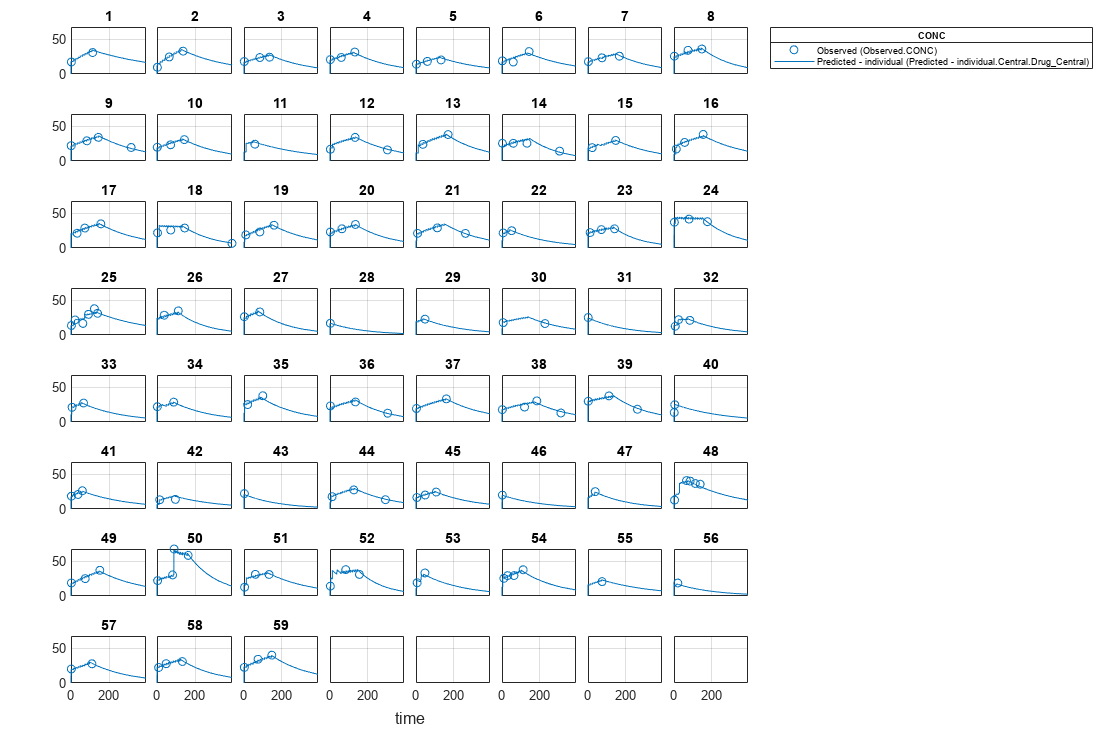
Visualize Results
Visualize the fitted results using individual-specific parameter estimates.
plot(nlmeResults_cov,'ParameterType','individual');
Use New Covariate Data to Evaluate the Fitted Model
Suppose you want to explore the responses of infants 1 and 2 using different covariate data, namely WEIGHT. You can do this by specifying the new WEIGHT data. The ID variable of the data corresponds to individual infants.
newData = data(data.ID == 1 | data.ID == 2,:); newData.WEIGHT(newData.ID == 1) = 1.3; newData.WEIGHT(newData.ID == 2) = 1.4;
Simulate the responses of infants 1 and 2 using the new covariate data.
[newResults_cov, newEstimates] = predict(nlmeResults_cov,newData,[dose1;dose2]);
newEstimates contains the updated parameter estimates for each individual (infants 1 and 2) after the model is reevaluated using the new covariate data.
newEstimates
newEstimates=4×3 table
Group Name Estimate
_____ ______________ _________
1 {'Central' } 2.5596
1 {'Cl_Central'} 0.0065965
2 {'Central' } 1.7123
2 {'Cl_Central'} 0.0064806
Compare to the estimated values from the original fit using the old covariate data.
nlmeResults_cov.IndividualParameterEstimates( ... nlmeResults_cov.IndividualParameterEstimates.Group == '1' | ... nlmeResults_cov.IndividualParameterEstimates.Group == '2',:)
ans=4×3 table
Group Name Estimate
_____ ______________ _________
1 {'Central' } 2.6988
1 {'Cl_Central'} 0.0070181
2 {'Central' } 1.8054
2 {'Cl_Central'} 0.0068948
Visualize the new simulation results together with the experimental data for infant 1 and 2.
figure; subplot(2,1,1); plot(data.TIME(data.ID == 1),data.CONC(data.ID == 1),'bo') hold on plot(newResults_cov(1).Time,newResults_cov(1).Data,'b') hold off ylabel('Concentration') legend('Observation(CONC)','Prediction','Location','NorthEastOutside') subplot(2,1,2) plot(data.TIME(data.ID == 2),data.CONC(data.ID == 2),'rx') hold on plot(newResults_cov(2).Time,newResults_cov(2).Data,'r') hold off legend('Observation(CONC)','Prediction','Location','NorthEastOutside') ylabel('Concentration') xlabel('Time')
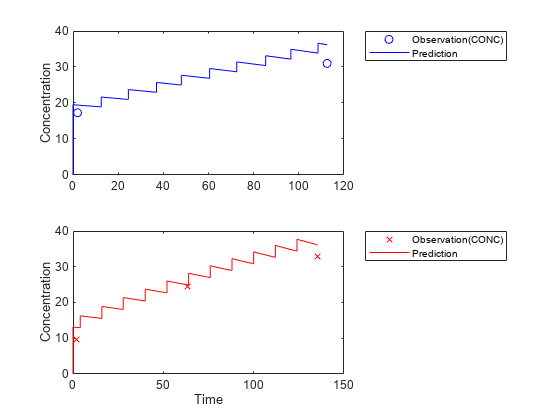
References
[1] Grasela, T. H. Jr., and S. M. Donn. "Neonatal population pharmacokinetics of phenobarbital derived from routine clinical data." Dev Pharmacol Ther 1985:8(6). 374-83.
This example uses data collected on 59 preterm infants given phenobarbital during the first 16 days after birth. Each infant received an initial dose followed by one or more sustaining doses by intravenous bolus administration. A total of between 1 and 6 concentration measurements were obtained from each infant at times other than dose times, for a total of 155 measurements. Infant weights and APGAR scores (a measure of newborn health) were also recorded. Data was described in [1], a study funded by the NIH/NIBIB grant P41-EB01975.
Load the data.
load pheno.mat ds
Visualize the data.
t = sbiotrellis(ds,'ID','TIME','CONC','marker','o','markerfacecolor',[.7 .7 .7],'markeredgecolor','r','linestyle','none'); t.plottitle = 'States versus Time';
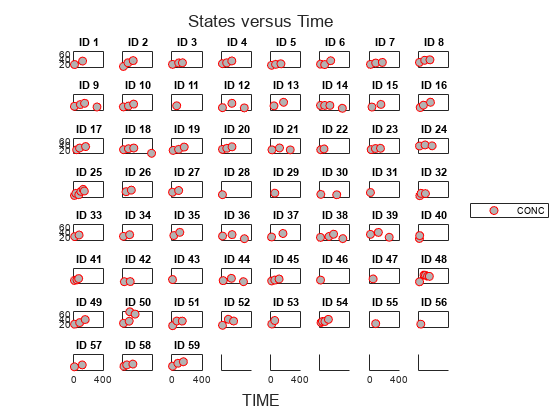
Create a one-compartment PK model with bolus dosing and linear clearance to model such data.
pkmd = PKModelDesign; pkmd.addCompartment('Central','DosingType','Bolus','EliminationType','linear-clearance',... 'HasResponseVariable',true,'HasLag',false); onecomp = pkmd.construct;
Suppose there is a correlation between the volume of the central compartment (Central) and the weight of infants. You can define this parameter-covariate relationship using a covariate model that can be described as
,
where, for each ith infant, V is the volume, θs (thetas) are fixed effects, η (eta) represents random effects, and WEIGHT is the covariate.
covM = CovariateModel;
covM.Expression = {'Central = exp(theta1+theta2*WEIGHT+eta1)'};Define the fixed and random effects. The column names of each table must have the names of fixed effects and random effects, respectively.
thetas = table(1.4,0.05,'VariableNames',{'theta1','theta2'}); eta1 = table(0.2,'VariableNames',{'eta1'});
Change the group label ID to GROUP as required by the sbiosampleparameters function.
ds.Properties.VariableNames{'ID'} = 'GROUP';Generate parameter values for the volumes of central compartments Central based on the covariate model for all infants in the data set.
phi = sbiosampleparameters(covM.Expression,thetas,eta1,ds);
You can then simulate the model using the sampled parameter values. For convenience, use the function-like interface provided by a SimFunction object.
First, construct a SimFunction object using the createSimFunction method, specifying the volume (Central) as the parameter, and the drug concentration in the compartment (Drug_Central) as the output of the SimFunction object, and the dosed species.
f = createSimFunction(onecomp,covM.ParameterNames,'Drug_Central','Drug_Central');
The data set ds contains dosing information for each infant, and the groupedData object provides a convenient way to extract such dosing information. Convert ds to a groupedData object and extract dosing information.
grpData = groupedData(ds);
doses = createDoses(grpData,'DOSE');Simulate the model using the sampled parameter values from phi and the extracted dosing information of each infant, and plot the results. The ith run uses the ith parameter value in phi and dosing information of the ith infant.
t = sbiotrellis(f(phi,200,doses.getTable),[],'TIME','Drug_Central'); % Resize the figure. t.hFig.Position(:) = [100 100 1280 800];
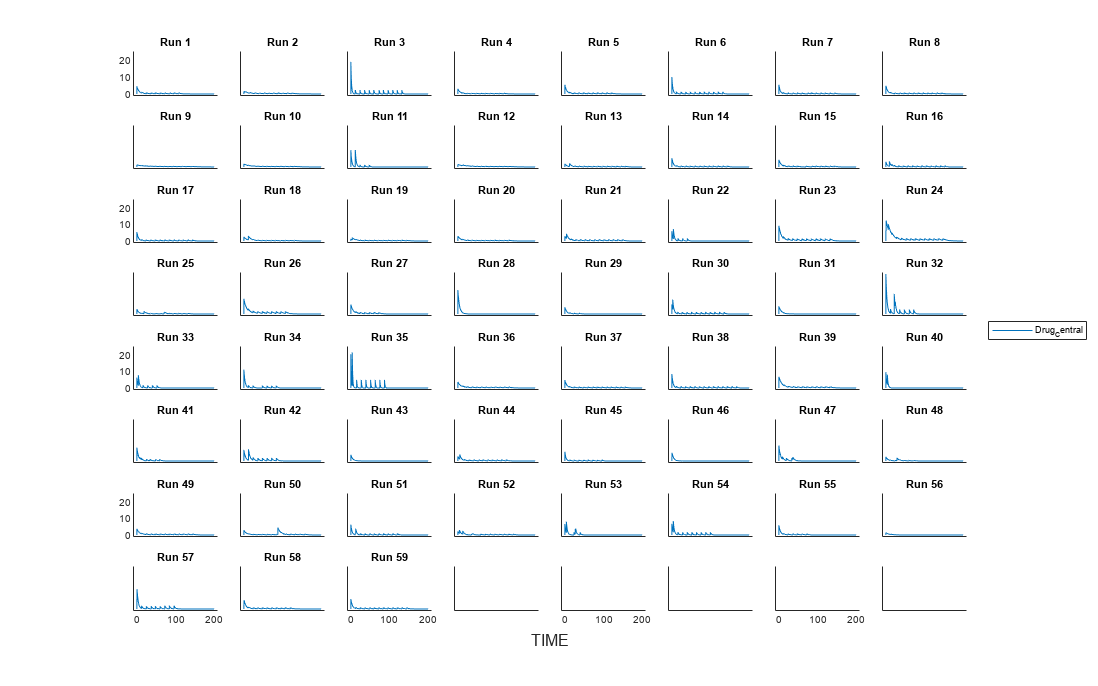
Version History
Introduced in R2011b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)