Systems and Models
The concepts in this topic provide a consistent and common language for using Simulink® software tools.
System
A system is a group of interdependent physical and functional parts with measurable characteristics that change over time.
For example, a vehicle is a system with multiple parts. Measurable characteristics include the linear speed of the vehicle and the rotational speed of the wheels.

System Component
A system component is part of a system that interacts with the other parts of the system. The interactions between components define the structure and behavior of the system.
For example, a cruise control module is a system component in a vehicle system. A microcontroller and the hardware associated with it define the structure while a software algorithm to control speed defines the behavior.

Model
A model is a mathematical description of a system derived either from physical laws or experimental data. The description typically uses a set of variables with a set of differential and difference equations that define the relationships between the variables.
In the following example for a vehicle, u(t) is the force (N)
moving a vehicle forward, v(t) is the velocity (m/s),
b is a drag coefficient (Nׂׂ·s/m), and m is
the mass of the vehicle (kg).

The vehicle is a continuous system. For continuous systems, differential equations
describe the rate of change for variables with the equations defined for all values of
time. The velocity of the vehicle v(t)and its acceleration
v'(t) are defined with the following first order differential
equation.
![]()
mv'(t) + bv(t) = u(t)
You can create a Simulink model for this equation by adding blocks, specifying block behavior, and using signal lines to connect the blocks to each other. The following Simulink block diagram implements the differential equation.
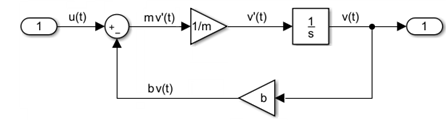
Model Component
A model component is part of a model that interacts with the other parts through an interface of inputs and outputs. Simulink implements model components using Subsystem and Model blocks. A Model block references another Simulink model saved in a separate file.
In the following example, the control model was saved in the Simulink model file control_model.slx, and then referenced from
a Model block in a second Simulink model. A Subsystem block was added for modeling the vehicle
mechanics.
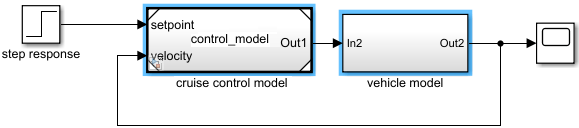
Typically, controllers are built with discrete systems using a computer to implement the control algorithm. For discrete systems, difference equations describe the rate of change for variables defined only at specific times. For example, the control signal for a simple discrete PI (proportional–integral) controller can be defined with the following difference equation.
![]()
PI[n] = e[n]Kp +
(e[n]+integral[n-1])Ki
Where e[n] is the error between a signal whose value is controlled
(velocity) and the specified value (set velocity), Kp is the
proportion constant, Ki is the integration constant, and
n is the time step.
The following Simulink block diagram implements the difference equation.
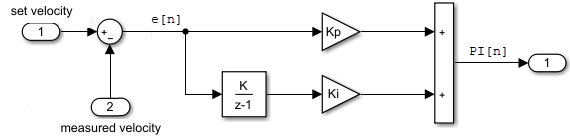
See also: Model a Continuous System, Component-Based Modeling Guidelines, Create Custom Library, Model Reference Behavior and Capabilities.
Differential Algebraic Equations
Some systems of equations contain additional constraints that involve the independent variable and the state vector in addition to differential equations. Such systems are called differential algebraic equations (DAEs).
The term algebraic refers to equations that do not involve derivatives.
In Simulink models, algebraic loops represent algebraic constraints. Models with algebraic loops define a system of differential algebraic equations.
For example, consider this model that implements a simple system of DAEs. The inner loop represents an algebraic constraint, while the outer loop represents a differential equation.
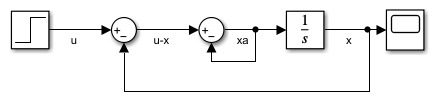
The model implements this system of DAEs.
x' = xa
0 = u - x - 2xa