Effects of Time-Varying Source Blocks on Frequency Response Estimation
Time-varying source blocks in a Simulink® model can interfere with frequency response estimation by driving the model away from the steady-state operating point of the system. To facilitate frequency response estimation, you can disable time-varying source blocks by setting them to constant values for estimation.
You can identify time-varying sources when estimating frequency responses at the command line and when using the Model Linearizer app.
To find source blocks, the software traces every signal path that can affect the signal value at each linearization output point in the model. The traced signal paths:
Signal paths inside virtual and nonvirtual subsystems.
Signal paths inside normal-mode referenced models. To ensure that the algorithm identifies source blocks within referenced models, set all referenced models to normal simulation mode before finding time-varying sources.
Signals routed through From and Goto blocks, or through Data Store Read and Data Store Write blocks.
Signals routed through switches. The software algorithm assumes that any pole of a switch can be active during frequency response estimation. The algorithm therefore follows the signal back through all switch inputs.
Some time-varying source blocks might not be found by the algorithm. If the internal
signal path of a block does not contain a block with no input port, that block is not reported
by the frest.findSources function or in the app. To
bring the model to steady state, replace the source block with a Constant block, or a different source block.
Set Time-Varying Sources to Constant for Estimation Using Model Linearizer
This example also shows how to improve estimation results by setting time-varying sources to be constant when estimating frequency responses using the Model Linearizer app.
Open the Simulink model.
openExample("scdspeed_ctrlloop")
Linearize the model.
Set the
Engine Modelblock to normal mode for accurate linearization.set_param("scdspeed_ctrlloop/Engine Model","SimulationMode","Normal")
Open the Model Linearizer for the model.
In the Simulink model window, in the Apps gallery, click Model Linearizer.
Click
 Bode to linearize the model and generate a Bode plot of the
result.
Bode to linearize the model and generate a Bode plot of the
result.The linearized model,
linsys1, appears in the Linear Analysis Workspace.
Create an input sinestream signal for the estimation.
Open the Create sinestream input dialog box.
On the Estimation tab, in the Input Signal drop-down list, select Sinestream.
Open the Add frequencies dialog box.
Click Add Frequencies.
Specify the input sinestream frequency range and number of frequency points.
Enter
10in the Min box.Enter
100in the Max box.Enter
10in the box for the number of frequency points.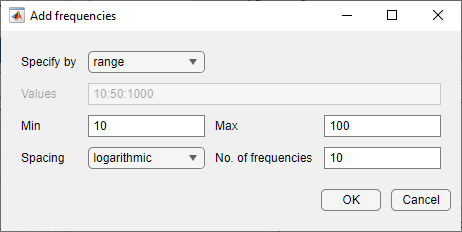
Click OK.
The added points are visible in the frequency content viewer of the Create sinestream input dialog box.
In the frequency content viewer of the Create sinestream input dialog box, select all the frequency points.
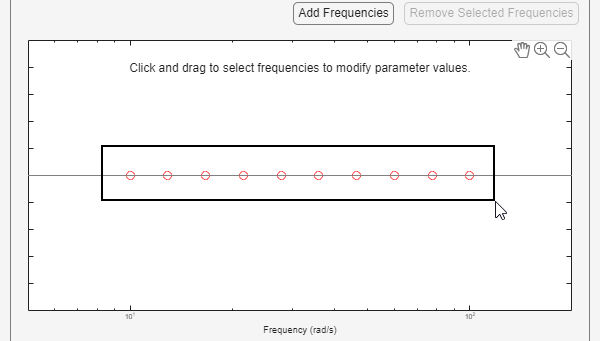
Specify input sinestream parameters.
Change the Number of periods and Settling periods to ensure that the model reaches steady-state for each frequency point in the input sinestream.
Enter
30in the Number of periods box.Enter
25in the Settling periods box.Create the input sinestream.
Click OK. The new input signal,
in_sine1, appears in the Linear Analysis Workspace.
Set the Diagnostic Viewer to open when estimation is performed.
On the Estimation tab, select Diagnostic Viewer.
Estimate the frequency response for the model.
Click
 Bode Plot 1 to estimate the frequency response. The
Diagnostic Viewer appears in the document area and the estimated system
Bode Plot 1 to estimate the frequency response. The
Diagnostic Viewer appears in the document area and the estimated system
estsys1appears in the Linear Analysis Workspace.Compare the estimated model and the linearized model.
In Bode Plot 1, there is one frequency point where the estimation and linearization do not match
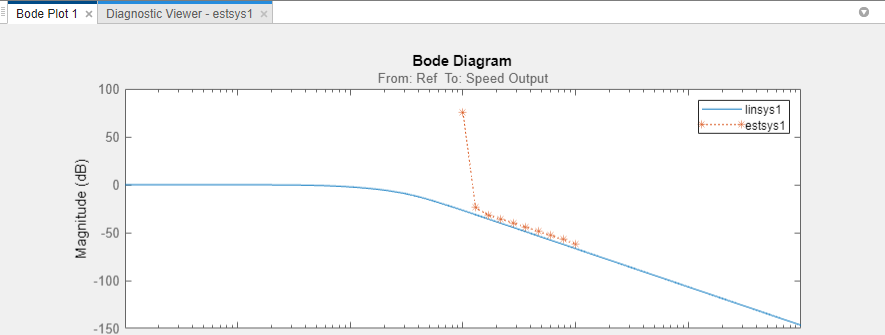
Click the Diagnostic Viewer tab in the plot area of the Model Linearizer.
Configure the Diagnostic Viewer to show only the frequency point where the estimation and linearization results do not match.
On the Diagnostic Viewer tab, in the Frequency Selector section, enter
9in the From box and11in the To box to set the frequency range that is analyzed in the Diagnostic Viewer.
The Filtered Steady State Time Response plot shows a signal that is not sinusoidal.
View the unfiltered time response.
Right-click the Filtered Steady State Time Response plot and clear the Show filtered steady state output only option.
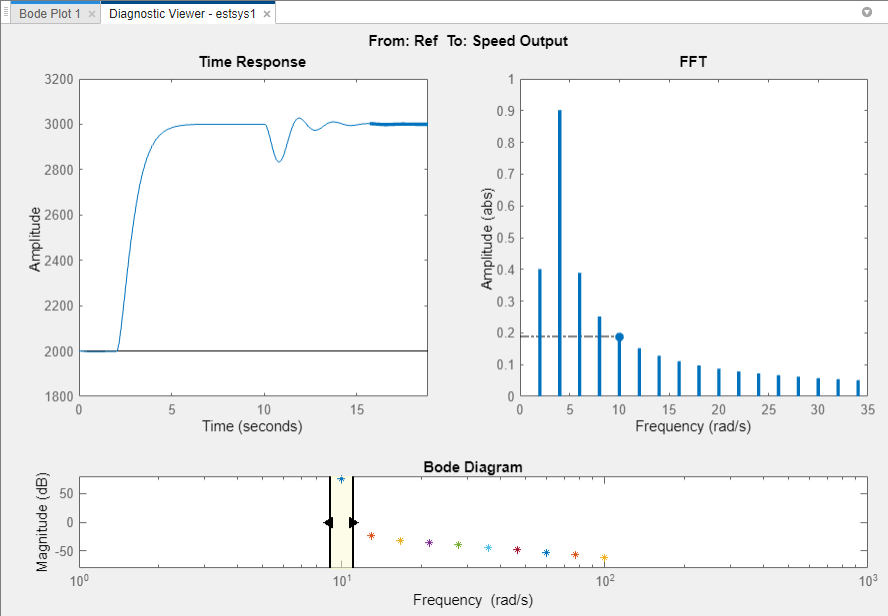
The step input and external disturbances drive the model away from the operating point used to linearize the model, which prevents the response from reaching steady-state. To correct this problem, find and disable the time-varying source blocks that interfere with the estimation. Then, estimate the frequency response of the model again.
Find and disable the time-varying sources within the model.
Open the Options for frequency response estimation dialog box.
On the Estimation tab, in the Options section, click More Options.

In the Options for frequency response estimation dialog box, on the Time Varying Sources tab, click Find and add time varying source blocks automatically.
This action populates the time varying sources list with the block paths of the time varying sources in the model. These sources will be held constant during estimation.

Close the dialog box.
Estimate the frequency response for the model.
On the estimation tab, click
 Bode Plot 1 to estimate the frequency response. The estimated
system
Bode Plot 1 to estimate the frequency response. The estimated
system estsys2, appears in the Linear Analysis Workspace.Compare the newly estimated model and the linearized model.
In Bode Plot 1, the magnitude response of
estsys1matches the exact linearization.
Set Time-Varying Sources to Constant for Estimation at the Command Line
This example also shows how to improve estimation results by setting time-varying
sources to be constant when estimating frequency responses using the
frestimate function.
Open the Simulink model.
openExample("scdspeed_ctrlloop")
Obtain the linear analysis points from the model.
io = getlinio(mdl);
Set the Engine Model subsystem to normal mode for accurate simulation results.
set_param("scdspeed_ctrlloop/Engine Model","SimulationMode","Normal")
Linearize the model.
sys = linearize(mdl,io);
Estimate the frequency response between 10 and 100 rad/s.
in = frest.Sinestream(... "Frequency",logspace(1,2,10),... "NumPeriods",30, "SettlingPeriods",25); [sysest,simout] = frestimate(mdl,io,in);
Compare the estimation results sysest with the exact linearization
sys.
frest.simView(simout,in,sysest,sys)
To view the unfiltered time response for the first frequency point, in the Simulation Results Viewer:
In the Bode Diagram section, adjust the shaded frequency range to contain only the first frequency point, which does not match the exact linearization at that frequency.
In the Time Response section, right click the plot and clear the Show filtered steady state output only parameter.
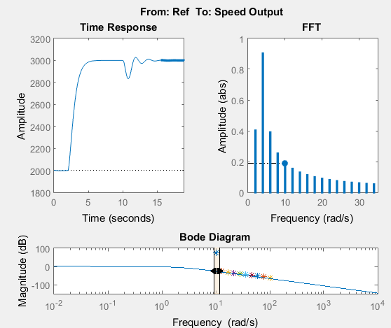
The step input and external disturbances drive the model away from the operating point, preventing the response from reaching steady-state. To correct this problem, find and disable the time-varying source blocks that interfere with the estimation.
Identify the time-varying source blocks using frest.findSources.
srcblks = frest.findSources(mdl,io);
Create a frequency response estimation option set to disable the blocks.
opts = frestimateOptions; opts.BlocksToHoldConstant = srcblks;
Repeat the frequency response estimation using the specified options.
[sysest2,simout2] = frestimate(mdl,io,in,opts); frest.simView(simout2,in,sysest2,sys)
In the Bode Diagram section, the estimated frequency response matches the exact linearization.
View the unfiltered time response for the first frequency point. In the Simulation Results Viewer:
In the Bode Diagram section, adjust the shaded frequency range to contain only the first frequency point.
In the Time Response section, right click the plot and clear the Show filtered steady state output only parameter.
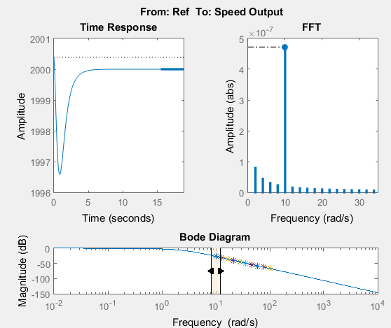
As shown in the Time Response plot, the system remains near the initial operating point.