Selecting a Measurement Frame
You can use the Transform Sensor block to measure the relative relationship between two arbitrary frames that are connected to the B and F frame ports of the block. The relationship includes relative rotation, translation, and their first and second time derivatives. These measurements are 3-D vectors or higher dimensioned quantities, such as rotation matrices.
To do computation with the measured vectors, the vectors must be expressed in
coordinates. The setting of Measurement Frame parameter
determines where to express the measured vectors; the vectors are expressed in the
selected frame's coordinates. For example, in the figure, because
Measurement Frame was set to
World, the Transform
Sensor block expresses a translation vector, shown as a black
arrow, in the world frame's coordinates.

Note
The rotation measurement of the Transform Sensor block is independent of the Measurement Frame parameter.
Measurement Frames
You can set the Measurement Frame parameter to
World, Base,
Follower, Non-Rotating
Base, or Non-Rotating
Follower.
World
The Transform Sensor block expresses and observes the measured vectors by using the world frame. For an example, see World.
The world frame is an inertial frame.
Base or Follower
The Transform Sensor block expresses and observes the measured vectors by using the selected base or follower frame.
The base or follower frame is the frame that connects to the block's B or F port, respectively. The base and follower frames are non-inertial. Therefore, the vectors expressed in the base or follower frame may involve centripetal and Coriolis terms.
Non-Rotating Base or Non-Rotating Follower
The Transform Sensor block maps the vectors expressed in the world frame to the selected frame that is non-rotating base or non-rotating follower frame. In other words, the block calculates the rotation matrix from the world frame to the current base or follower frame then multiplies the matrix with the vectors expressed in the world frame.
The non-rotating base or non-rotating follower frame is an instantaneous frame that is coincident and aligned with the corresponding base or follower frame at the current time. The measurements expressed in the non-rotating frames do not involve centripetal and Coriolis terms.
The table compares the properties of the measurements for the different Measurement Frame settings.
| Measurement Frame | Standard Derivative Relationship |
|---|---|
| World | Yes |
| Base | Yes |
| Follower | Yes |
| Non-Rotating Base | No |
| Non-Rotating Follower | No |
When a selected frame satisfies the standard derivative relationship, the
measurements expressed in this frame are related to each other. For example,
when you select World, the expressed linear
acceleration vector is the time derivative of the expressed linear velocity
vector, which is the time derivative of the expressed linear translation
vector.
Example
This example shows the measurements of the Transform Sensor block with different settings of the Measurement Frame parameter. The image illustrates a single degree-of-freedom system with four parts: a support, hub, rod, and car. The support is fixed on the ground, and the rod connects the hub and car. The base, follower, and world frames of the system are located at the center of the hub, car, and support’s bottom, respectively. Note that the world and base frames are fixed frames and the follower frame moves with the car.

The rod has a length of and rotates with a constant angular velocity, , around the Z-axis of the base frame. A
Transform Sensor block is used to measure the
relative motions between the car and hub. For example, the block measures the
relative translation, and rotation, between the car and hub. The maps vectors in the follower frame to vectors in the base
frame.
The image shows the front view of the system. For simplicity purposes, this example only shows how to express linear measurements, such as translation, velocity, and acceleration, in Cartesian coordinates.

World
When you set Measurement Frame to World, the
block measures the motion of the follower frame with respect to the base
frame then expresses and observes the relative motion by using the world
frame.
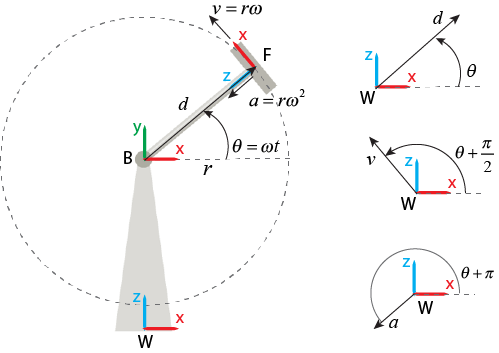
The translation, velocity, and acceleration vectors have constant magnitudes because the
length of the rod and the rotational speed are constant. However, they
rotate with a constant rotational velocity, , around the Y-axis of the world frame.
Therefore, the translation, velocity, and acceleration vectors can be
observed as:
Note that the vectors expressed in the world frame always satisfy the standard derivative relationship. For example, equals the time derivative of .
Base or Follower
When you set Measurement Frame to Base, the
block measures the relative motion of the follower frame with respect to the
base frame then expresses and observes the relative motion by using the base
frame.

Because the base frame is fixed in this example, the measurements can be observed as:
When you set Measurement Frame to Follower,
the block measures the relative motion of the follower frame to the base
frame then expresses and observes the relative motion by using the follower
frame. The expressed vectors include centripetal and Coriolis terms because
the follower frame rotates over time. To an observer attached to the
follower frame, the origin of the base frame never moves. Therefore, the
offset between the base and follower frames is constant, and the relative
linear velocity and linear acceleration are zero.
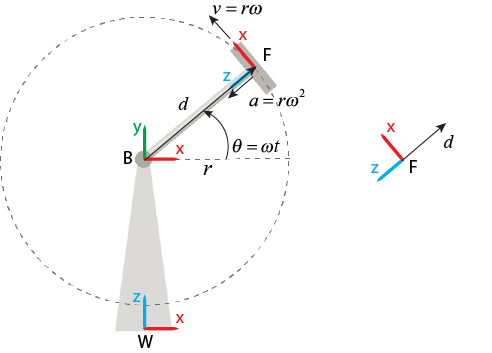
Note that the vectors expressed in the base and follower frames always satisfy the standard derivative relationship. For example, equals the time derivative of .
Non-Rotating Base or Non-Rotating Follower
When you set Measurement Frame to Non-Rotating
Base, the block maps the vectors expressed in the world
frame to an instantaneous frame that is coincident and aligned with the base
frame at the current moment.
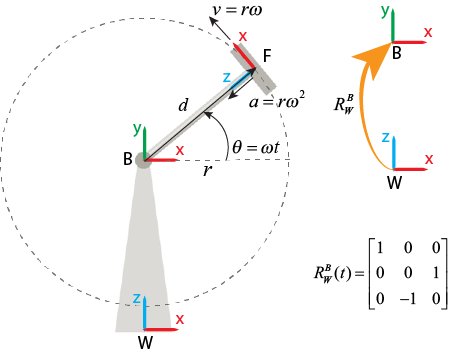
When you set Measurement Frame to Non-Rotating
Follower, the block maps the vectors expressed in the
world frame to an instantaneous frame that is coincident and aligned with
the follower frame at the current moment.

Note that if a base or follower frame is not fixed, the measurements in its corresponding
non-rotating frame do not satisfy the standard derivative relationship. For
example, because the follower frame rotates, if you set
Measurement Frame to Non-Rotating
Follower, the expressed velocity vector is not the time
derivative of the expressed translation vector.