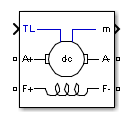
DC Machine
(To be removed) Implement wound-field or permanent magnet DC machine
The Specialized Power Systems library will be removed in R2026a. Use the Simscape™ Electrical™ blocks and functions instead. For more information on updating your models, see Upgrade Specialized Power System Models to use Simscape Electrical Blocks.
Libraries:
Simscape /
Electrical /
Specialized Power Systems /
Electrical Machines
Description
The DC Machine block implements a wound-field or permanent magnet DC machine.
For the wound-field DC machine, you can access the field terminals (F+, F−) to use the machine model as a shunt-connected or a series-connected DC machine. The Simulink® input TL provides the torque applied to the shaft.
The armature circuit (A+, A−) consists of an inductor La and resistor Ra in series with a counter-electromotive force (CEMF) E.
The CEMF is proportional to the machine speed.
| E = KEω | (1) |
KE is the voltage constant and ω is the machine speed.
In a separately excited DC machine model, the voltage constant KE is proportional to the field current If:
| KE = LafIf, | (2) |
Laf is the field-armature mutual inductance.
The electromechanical torque that the DC Machine block develops is proportional to the armature current Ia.
| Te = KTIa, | (3) |
KT is the torque constant. The sign convention for Te and TL is:
| Te ,
TL > 0: Motor
mode Te, TL < 0: Generator mode | (4) |
The torque constant is equal to the voltage constant.
| KT = KE. | (5) |
The armature circuit is connected between the A+ and A− ports of the DC Machine block. It is represented by a series Ra La branch in series with a Controlled Voltage Source and a Current Measurement block.
In the wound-field DC machine model, the field circuit is represented by an RL circuit. It is connected between the F+ and F− ports of the DC Machine block.
In the permanent magnet DC machine model, there is no field current as the magnets establish the excitation flux. KE and KT are constants.
The mechanical part computes the speed of the DC machine from the net torque applied to the rotor. The block uses the speed to implement the CEMF voltage E of the armature circuit.
The mechanical part implements this equation:
where J is the inertia, Bm is the viscous friction coefficient, and Tf is the Coulomb friction torque.
Ports
Input
Output
Conserving
Parameters
References
[1] Analysis of Electric Machinery, Krause et al., pp. 89–92.
Extended Capabilities
Version History
Introduced before R2006a