SM AC5C
Discrete-time or continuous-time synchronous machine AC5C excitation system including an automatic voltage regulator and an exciter
Libraries:
Simscape /
Electrical /
Control /
SM Control
Description
The SM AC5C block implements a synchronous machine type AC5C excitation system model in conformance with IEEE 421.5-2016[1].
Use this block to model the control and regulation of the field voltage of a synchronous machine that operates as a generator using an AC rotating exciter.
You can switch between continuous and discrete implementations of the block by using the
Sample time (-1 for inherited) parameter. To configure the
integrator for continuous time, set the Sample time (-1 for
inherited) property to 0. To configure the integrator
for discrete time, set the Sample time (-1 for inherited) property
to a positive, nonzero value, or to -1 to inherit the sample time
from an upstream block.
The SM AC5C block is made up of four major components:
The Current Compensator modifies the measured terminal voltage as a function of terminal current.
The Voltage Measurement Transducer simulates the dynamics of a terminal voltage transducer using a low-pass filter.
The Excitation Control Elements component compares the voltage transducer output with a terminal voltage reference to produce a voltage error. This voltage error is then passed through a voltage regulator to produce the exciter field voltage.
The AC Rotating Exciter models the AC rotating exciter, which produces a field voltage that is applied to the controlled synchronous machine. The block also feeds the exciter field current (which is given the standard symbol VFE) back to the excitation system.
This diagram shows the overall structure of the AC5C excitation system model:

In the diagram:
VT and IT are the measured terminal voltage and current of the synchronous machine.
VC1 is the current-compensated terminal voltage.
VC is the filtered, current-compensated terminal voltage.
VREF is the reference terminal voltage.
VS is the power system stabilizer voltage.
EFE and VFE are the exciter field voltage and current, respectively.
EFD and IFD are the field voltage and current, respectively.
The following sections describe each of the major parts of the block in detail.
Current Compensator and Voltage Measurement Transducer
The current compensator is modeled as:
where:
RC is the load compensation resistance.
XC is the load compensation reactance.
The voltage measurement transducer is implemented as a Low-Pass Filter block with time constant TR. Refer to the documentation for this block for the discrete and continuous implementations.
Excitation Control Elements
This diagram illustrates the overall structure of the excitation control elements:
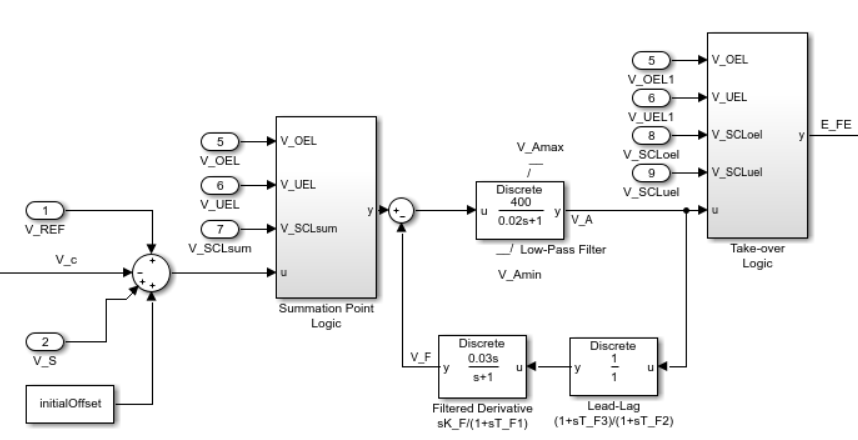
In the diagram:
The Summation Point Logic subsystem models the summation point input location for the overexcitation limiter (OEL), underexcitation limiter (UEL), and stator current limiter (SCL) voltages. For more information about using limiters with this block, see Field Current Limiters.
The Low-Pass Filter block models the major dynamics of the voltage regulator. Here, KA is the regulator gain and TA is the major time constant of the regulator. The minimum and maximum anti-windup saturation limits for the block are VAmin and VAmax, respectively.
The Filtered Derivative and the Lead-Lag blocks model the rate feedback path for stabilization of the excitation system. Here, KF is the gain of this system and TF1, TF2, and TF3 are its time constants. Refer to the documentation for the Filtered Derivative block for the discrete and continuous implementations.
The Take-over Logic subsystem models the take-over point input location for the OEL, UEL, and SCL voltages. For more information about using limiters with this block, see Field Current Limiters.
The initialOffset Constant block ensures the simulation can start from a steady state. The SM AC5C block calculates this value by using saturation and exciter parameters, including the initial field voltage and the regulator output gain.
Field Current Limiters
You can use various field current limiters to modify the output of the voltage regulator under unsafe operating conditions:
Use an overexcitation limiter to prevent overheating of the field winding due to excessive field current demand.
Use an underexcitation limiter to boost field excitation when it is too low, which risks desynchronization.
Use a stator current limiter to prevent overheating of the stator windings due to excessive current.
Attach the output of any of these limiters at one of these points:
The summation point as part of the automatic voltage regulator (AVR) feedback loop
The take-over point to override the usual behavior of the AVR
If you are using the stator current limiter at the summation point, use the single input VSCLsum. If you are using the stator current limiter at the take-over point, use both the overexcitation input, VSCLoel and the underexcitation input, VSCLuel.
AC Rotating Exciter
This diagram shows the structure of the AC rotating exciter:

In the diagram:
The exciter field current VFE is the sum of three signals:
The nonlinear function Vx models the saturation of the exciter output voltage.
The proportional term KE models the linear relationship between the exciter output voltage and the exciter field current.
The subsystem models the demagnetizing effect of the load current on the exciter output voltage using the demagnetization constant KD in the feedback loop.
The Integrator with variable limits subsystem integrates the difference between EFE and VFE to generate the exciter alternator output voltage VE. TE is the time constant for this process.
The nonlinear function FEX models the exciter output voltage drop from the rectifier regulation. This function depends on the constant KC, which itself is a function of commutating reactance.
The parameters VEmin and VFEmax model the lower and upper limits of the rotating exciter.
Ports
Input
Output
Parameters
References
[1] IEEE Recommended Practice for Excitation System Models for Power System Stability Studies. IEEE Std 421.5-2016. Piscataway, NJ: IEEE-SA, 2016.
Extended Capabilities
Version History
Introduced in R2020a
