loss

Classification error

Syntax

L = loss(obj,X,Y)
L = loss(obj,X,Y,Name,Value)


Description

L = loss(obj,X,Y) returns the classification loss, which is a scalar representing how well obj classifies the data in X, when Y contains the true classifications.

When computing the loss, loss normalizes the class probabilities in Y to the class probabilities used for training, stored in the Prior property of obj.

L = loss(obj,X,Y,Name,Value) returns the loss with additional options specified by one or more Name,Value pair arguments.

Note

If the predictor data X contains any missing values and LossFun is not set to "mincost" or "classiferror", the loss function can return NaN. For more information, see loss can return NaN for predictor data with missing values.

Input Arguments

obj	Discriminant analysis classifier of class ClassificationDiscriminant or CompactClassificationDiscriminant, typically constructed with fitcdiscr.
X	Matrix where each row represents an observation, and each column represents a predictor. The number of columns in X must equal the number of predictors in obj.
Y	Class labels, with the same data type as exists in obj. The number of elements of Y must equal the number of rows of X.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

LossFun

Built-in loss function name (character vector or string scalar in the table) or function handle. The following table lists the available loss functions. Specify one using the corresponding value. Value Description 'binodeviance' Binomial deviance 'classifcost' Observed misclassification cost 'classiferror' Misclassified rate in decimal 'exponential' Exponential loss 'hinge' Hinge loss 'logit' Logistic loss 'mincost' Minimal expected misclassification cost (for classification scores that are posterior probabilities) 'quadratic' Quadratic loss 'mincost' is appropriate for classification scores that are posterior probabilities. Discriminant analysis models return posterior probabilities as classification scores by default (see predict). Specify your own function using function handle notation. Suppose that n be the number of observations in X and K be the number of distinct classes (numel(Mdl.ClassNames)). Your function must have this signature lossvalue = lossfun(C,S,W,Cost) where: The output argument lossvalue is a scalar. You choose the function name (lossfun). C is an n-by-K logical matrix with rows indicating which class the corresponding observation belongs. The column order corresponds to the class order in Mdl.ClassNames. Construct C by setting C(p,q) = 1 if observation p is in class q, for each row. Set all other elements of row p to 0. S is an n-by-K numeric matrix of classification scores. The column order corresponds to the class order in Mdl.ClassNames. S is a matrix of classification scores, similar to the output of predict. W is an n-by-1 numeric vector of observation weights. If you pass W, the software normalizes them to sum to 1. Cost is a K-by-K numeric matrix of misclassification costs. For example, Cost = ones(K) - eye(K) specifies a cost of 0 for correct classification, and 1 for misclassification. Specify your function using 'LossFun',@lossfun. For more details on loss functions, see Classification Loss. Default: 'mincost'

Weights

Numeric vector of length N, where N is the number of rows of X. weights are nonnegative. loss normalizes the weights so that observation weights in each class sum to the prior probability of that class. When you supply weights, loss computes weighted classification loss. Default: ones(N,1)

Output Arguments

L	Classification loss, a scalar. The interpretation of L depends on the values in weights and lossfun.

Examples

Estimate Classification Error

Load Fisher's iris data set.

load fisheriris

Train a discriminant analysis model using all observations in the data.

Mdl = fitcdiscr(meas,species);

Estimate the classification error of the model using the training observations.

L = loss(Mdl,meas,species)

L = 0.0200

Alternatively, if Mdl is not compact, then you can estimate the training-sample classification error by passing Mdl to resubLoss.

More About

Classification Loss

Classification loss functions measure the predictive inaccuracy of classification models. When you compare the same type of loss among many models, a lower loss indicates a better predictive model.

Consider the following scenario.

• L is the weighted average classification loss.

• n is the sample size.

• For binary classification:

  • y_j is the observed class label. The software codes it as –1 or 1, indicating the negative or positive class (or the first or second class in the ClassNames property), respectively.

  • f(X_j) is the positive-class classification score for observation (row) j of the predictor data X.

  • m_j = y_jf(X_j) is the classification score for classifying observation j into the class corresponding to y_j. Positive values of m_j indicate correct classification and do not contribute much to the average loss. Negative values of m_j indicate incorrect classification and contribute significantly to the average loss.

• For algorithms that support multiclass classification (that is, K ≥ 3):

  • y_j^* is a vector of K – 1 zeros, with 1 in the position corresponding to the true, observed class y_j. For example, if the true class of the second observation is the third class and K = 4, then y₂^* = [0 0 1 0]′. The order of the classes corresponds to the order in the ClassNames property of the input model.

  • f(X_j) is the length K vector of class scores for observation j of the predictor data X. The order of the scores corresponds to the order of the classes in the ClassNames property of the input model.

  • m_j = y_j^*′f(X_j). Therefore, m_j is the scalar classification score that the model predicts for the true, observed class.

• The weight for observation j is w_j. The software normalizes the observation weights so that they sum to the corresponding prior class probability stored in the Prior property. Therefore,

  $${\displaystyle \sum _{j=1}^n{w}_j}=1.$$

Given this scenario, the following table describes the supported loss functions that you can specify by using the LossFun name-value argument.

Loss Function	Value of LossFun	Equation
Binomial deviance	'binodeviance'	$$L={\displaystyle \sum _{j=1}^n{w}_j\log \left\{1+\exp \left[-2m_j\right]\right\}}.$$
Observed misclassification cost	'classifcost'	$$L={\displaystyle \sum _{j=1}^n{w}_j}{c}_{y_j{\widehat{y}}_j},$$ where $${\widehat{y}}_j$$ is the class label corresponding to the class with the maximal score, and $$c_{y_j{\widehat{y}}_j}$$ is the user-specified cost of classifying an observation into class $${\widehat{y}}_j$$ when its true class is yj.
Misclassified rate in decimal	'classiferror'	$$L={\displaystyle \sum _{j=1}^n{w}_j}I\left\{{\widehat{y}}_j\ne y_j\right\},$$ where I{·} is the indicator function.
Cross-entropy loss	'crossentropy'	'crossentropy' is appropriate only for neural network models. The weighted cross-entropy loss is $$L=-{\displaystyle \sum _{j=1}^n\frac{{\tilde{w}}_j\log (m_j)}{Kn}},$$ where the weights $${\tilde{w}}_j$$ are normalized to sum to n instead of 1.
Exponential loss	'exponential'	$$L={\displaystyle \sum _{j=1}^n{w}_j\exp \left(-m_j\right)}.$$
Hinge loss	'hinge'	$$L={\displaystyle \sum }_{j=1}^n{w}_j\max \left\{0,1-m_j\right\}.$$
Logit loss	'logit'	$$L={\displaystyle \sum _{j=1}^n{w}_j\log \left(1+\exp \left(-m_j\right)\right)}.$$
Minimal expected misclassification cost	'mincost'	'mincost' is appropriate only if classification scores are posterior probabilities. The software computes the weighted minimal expected classification cost using this procedure for observations j = 1,...,n. Estimate the expected misclassification cost of classifying the observation Xj into the class k: $${\gamma }_{jk}={\left(f{\left(X_j\right)}^{\prime }C\right)}_k.$$ f(Xj) is the column vector of class posterior probabilities for the observation Xj. C is the cost matrix stored in the Cost property of the model. For observation j, predict the class label corresponding to the minimal expected misclassification cost: $${\widehat{y}}_j=\underset{k=1,\mathrm{...},K}{\text{argmin}}{\gamma }_{jk}.$$ Using C, identify the cost incurred (cj) for making the prediction. The weighted average of the minimal expected misclassification cost loss is $$L={\displaystyle \sum _{j=1}^n{w}_j{c}_j}.$$
Quadratic loss	'quadratic'	$$L={\displaystyle \sum _{j=1}^n{w}_j{\left(1-m_j\right)}^2}.$$

If you use the default cost matrix (whose element value is 0 for correct classification and 1 for incorrect classification), then the loss values for 'classifcost', 'classiferror', and 'mincost' are identical. For a model with a nondefault cost matrix, the 'classifcost' loss is equivalent to the 'mincost' loss most of the time. These losses can be different if prediction into the class with maximal posterior probability is different from prediction into the class with minimal expected cost. Note that 'mincost' is appropriate only if classification scores are posterior probabilities.

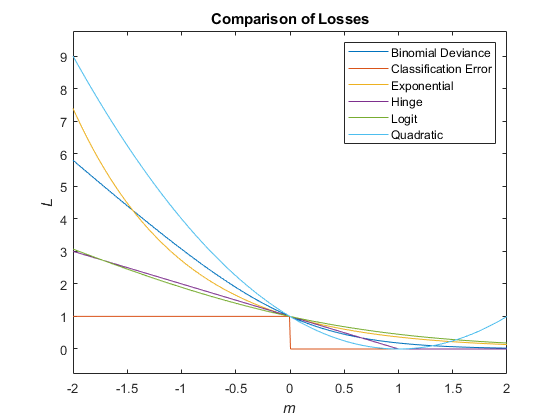
This figure compares the loss functions (except 'classifcost', 'crossentropy', and 'mincost') over the score m for one observation. Some functions are normalized to pass through the point (0,1).

Posterior Probability

The posterior probability that a point x belongs to class k is the product of the prior probability and the multivariate normal density. The density function of the multivariate normal with 1-by-d mean μ_k and d-by-d covariance Σ_k at a 1-by-d point x is

$$P\left(x|k\right)=\frac{1}{{\left({\left(2\pi \right)}^d\left|{\Sigma }_k\right|\right)}^{1/2}}\exp \left(-\frac{1}{2}\left(x-{\mu }_k\right){\Sigma }_k^{-1}{\left(x-{\mu }_k\right)}^T\right),$$

where $$\left|{\Sigma }_k\right|$$ is the determinant of Σ_k, and $${\Sigma }_k^{-1}$$ is the inverse matrix.

Let P(k) represent the prior probability of class k. Then the posterior probability that an observation x is of class k is

$$\widehat{P}\left(k|x\right)=\frac{P\left(x|k\right)P\left(k\right)}{P\left(x\right)},$$

where P(x) is a normalization constant, the sum over k of P(x|k)P(k).

Prior Probability

The prior probability is one of three choices:

• 'uniform' — The prior probability of class k is one over the total number of classes.

• 'empirical' — The prior probability of class k is the number of training samples of class k divided by the total number of training samples.

• Custom — The prior probability of class k is the kth element of the prior vector. See fitcdiscr.

After creating a classification model (Mdl) you can set the prior using dot notation:

Mdl.Prior = v;

where v is a vector of positive elements representing the frequency with which each element occurs. You do not need to retrain the classifier when you set a new prior.

Cost

The matrix of expected costs per observation is defined in Cost.

Extended Capabilities

Tall Arrays

Calculate with arrays that have more rows than fit in memory.

This function fully supports tall arrays. You can use models trained on either in-memory or tall data with this function.

For more information, see Tall Arrays.

Version History

R2022a: loss can return NaN for predictor data with missing values

Behavior changed in R2022a

The loss function no longer omits an observation with a NaN score when computing the weighted average classification loss. Therefore, loss can now return NaN when the predictor data X contains any missing values and the name-value argument LossFun is not specified as "classifcost", "classiferror", or "mincost". In most cases, if the test set observations do not contain missing predictors, the loss function does not return NaN.

This change improves the automatic selection of a classification model when you use fitcauto. Before this change, the software might select a model (expected to best classify new data) with few non-NaN predictors.

If loss in your code returns NaN, you can update your code to avoid this result by doing one of the following:

• Remove or replace the missing values by using rmmissing or fillmissing, respectively.

• Specify the name-value argument LossFun as "classifcost", "classiferror", or "mincost".

The following table shows the classification models for which the loss object function might return NaN. For more details, see the Compatibility Considerations for each loss function.

Model Type	Full or Compact Model Object	loss Object Function
Discriminant analysis classification model	ClassificationDiscriminant, CompactClassificationDiscriminant	loss
Ensemble of learners for classification	ClassificationEnsemble, CompactClassificationEnsemble	loss
Gaussian kernel classification model	ClassificationKernel	loss
k-nearest neighbor classification model	ClassificationKNN	loss
Linear classification model	ClassificationLinear	loss
Neural network classification model	ClassificationNeuralNetwork, CompactClassificationNeuralNetwork	loss
Support vector machine (SVM) classification model	ClassificationSVM, CompactClassificationSVM	loss