finv
F inverse cumulative distribution function
Syntax
Description
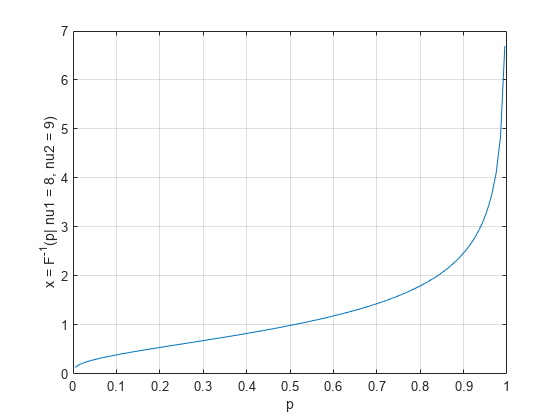
Examples
Input Arguments
Output Arguments
More About
Alternative Functionality
finvis a function specific to the F distribution. Statistics and Machine Learning Toolbox™ also offers the generic functionicdf, which supports various probability distributions. To useicdf, specify the probability distribution name and its parameters. Note that the distribution-specific functionfinvis faster than the generic functionicdf.
References
[1] Abramowitz, M., and I. A. Stegun. Handbook of Mathematical Functions. New York: Dover, 1964.
[2] Freund, John E. Mathematical Statistics Fifth Edition. Englewood Cliffs, NJ: Prentice Hall College Division, 1992.
Extended Capabilities
Version History
Introduced before R2006a