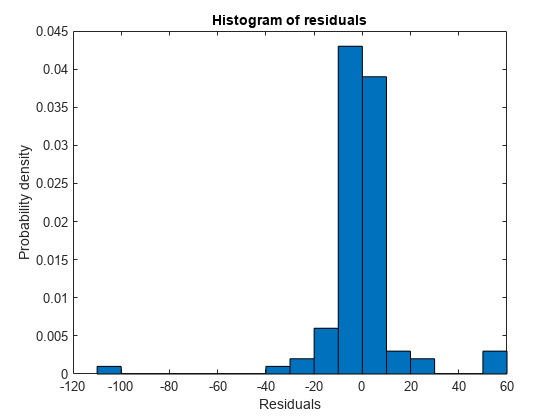
plotResiduals
Plot residuals of generalized linear regression model
Syntax
Description
plotResiduals( creates a histogram
plot of the generalized linear regression model (mdl)mdl)
residuals.
plotResiduals(
specifies additional options using one or more name-value pair arguments. For
example, you can specify the residual type and the graphical properties of residual
data points.mdl,plottype,Name,Value)
h = plotResiduals(___)h to modify the properties of a specific line or patch
after you create the plot. For a list of properties, see Line Properties and Patch Properties.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Tips
The data cursor displays the values of the selected plot point in a data tip (small text box located next to the data point). The data tip includes the x-axis and y-axis values for the selected point, along with the observation name or number.
Alternative Functionality
A GeneralizedLinearModel object provides multiple plotting functions.
When verifying a model, use
plotDiagnosticsto find questionable data and to understand the effect of each observation. Also, useplotResidualsto analyze the residuals of the model.After fitting a model, use
plotPartialDependenceto understand the effect of a particular predictor. Also, useplotSliceto plot slices through the prediction surface.