incrementalDynamicKMeans
Description
The incrementalDynamicKMeans function creates an
incrementalDynamicKMeans model object that is suitable for incremental dynamic
k-means clustering. incrementalDynamicKMeans allows you to update
the dynamic clustering model incrementally by supplying chunks of data to the incremental
fit function. To
perform incremental k-means clustering with a fixed number of clusters, use
incrementalKMeans.
When you call the incrementalDynamicKMeans function, you can specify clustering
options, such as the cluster growth penalty factor, the warm-up period, and whether to
standardize the training data before fitting the model to data. After you create an
incrementalDynamicKMeans object, it is prepared for incremental dynamic
k-means clustering. For more information, see Incremental Dynamic k-Means Clustering.
Creation
You can create an incrementalDynamicKMeans model object in two ways:
Call the function directly — Configure incremental dynamic k-means clustering options by calling
incrementalDynamicKMeansdirectly. This approach is best when you do not have data yet or you want to start incremental dynamic k-means clustering immediately. When you callincrementalDynamicKMeans, you can specify initial cluster centroids and cluster counts so that the initial model is warm.Call an incremental learning function — The
fitandupdateMetricsfunctions accept a configuredincrementalDynamicKMeansmodel object and data as input, and return anincrementalDynamicKMeansmodel object updated with information computed from the input model and data.
Syntax
Description
Mdl = incrementalDynamicKMeans(numClusters=k)
Mdl = incrementalDynamicKMeans(centroids=C)C.
Mdl = incrementalDynamicKMeans(___,Name=Value)Mdl=incrementalDynamicKMeans(numClusters=12,Distance="cityblock")
creates an incrementalDynamicKMeans model object that has 12 initial
clusters and uses the city block distance metric.
Input Arguments
Parameter for initial number of clusters, specified as a positive integer. The
software uses k to set the initial value of the NumClusters
and NumDynamicClusters properties.
If you specify k:
You cannot specify
C.If
MergeClustersisfalse(the default), the software setsNumClustersandNumDynamicClustersequal to j, where j ismax(k,max(1,ceil((k-15)/5))+NumAdditionalClusters). IfNumAdditionalClusters=10(the default), then j=11whenk≤10, and j=kotherwise.If
MergeClustersistrue, the software setsNumClusters=kandNumDynamicClusters=j.
Example: 10
Data Types: single | double
Initial cluster centroids, specified as an
n-by-p numeric matrix where each row contains
a cluster centroid, and each column contains the predictor values. The software uses
C to set the initial values of the following properties:
Centroids,
DynamicCentroids, NumClusters, and NumDynamicClusters.
If you specify C:
You cannot specify
korStandardizeData. The software setsStandardizeData=false.You cannot specify a nonzero value of
NumPredictors. If you specifyNumPredictors=0, the software setsNumPredictors=p.CentroidsandDynamicCentroidscontain the unique rows ofCand additional rows ofNaNvalues, ifCcontains nonunique rows.If you specify
MergeClusters=false(the default):The software sets
NumClustersandNumDynamicClustersequal to j, where j ismax(n,max(1,ceil((n-15)/5))+NumAdditionalClusters). IfNumAdditionalClusters=10(the default), then j=11whenn≤10, and j=kotherwise.CentroidsandDynamicCentroidsare j-by-p matrices that contain the unique rows ofCand additional rows ofNaNvalues.
If you specify
MergeClusters=true:The software sets
NumClusters=nandNumDynamicClusters=j.Centroidsis an n-by-p matrix that contains the unique rows ofCand additional rows ofNaNvalues.DynamicCentroidsis a j-by-p matrix that contains the unique rows ofCand additional rows ofNaNvalues.
Example: [2 4 5; 1 3 3; 2 5 1]
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: Mdl =
incrementalDynamicKMeans(numClusters=13,EstimationPeriod=1000,StandardizeData=true)
specifies to use 13 initial clusters, and to standardize the data using
an estimation period of 1000 observations.
Cluster counts, specified as a vector of positive integers. The software uses
ClusterCounts to set the initial values of the ClusterCounts and
DynamicClusterCounts properties. The software updates these properties
when you call the reset
function or the incremental fit
function. The incremental fit function uses
ClusterCounts to determine the learning rate when it updates
the cluster centroids.
If you specify ClusterCounts=counts when
you create Mdl:
You must specify
C.You cannot specify
korStandardizeData. The software setsStandardizeData=false.countsmust be a vector of positive integers with lengthsize(.C,1)ClusterCountsis aNumClusters-by-1 vector.The first m rows of
ClusterCountscontain the sum of thecountsvalues for each unique row ofC, ifCcontains nonunique rows and m unique rows. The remaining rows ofClusterCountscontain zeros.
If you do not specify ClusterCounts when you create
Mdl:
ClusterCountsis aNumClusters-by-1 vector of zeros, if you specifyk.ClusterCountsis aNumClusters-by-1 vector, if you specifyC. The first m rows ofClusterCountscontain the number of instances of each m unique row inC. The remaining rows ofClusterCountscontain zeros.
Example: ClusterCounts=[2 4 9 2 5 2 6 7]
Data Types: single | double
Number of predictors, specified as a nonnegative integer. This argument sets the NumPredictors
property.
If you specify
Cwhen you createMdl:You can only specify
NumPredictors=size(orC,2)NumPredictors=0The software sets
NumPredictors=size(if you do not specifyC,2)NumPredictorsor specifyNumPredictors=0
If you specify
kand do not specifyNumPredictorswhen you createMdl, the software setsNumPredictors=0.If
NumPredictors=0, the software infers the number of predictors from the training data and updatesNumPredictorswhen you call the incrementalfitfunction.
Example: NumPredictors=10
Data Types: single | double
Distance metric in p-dimensional space used for minimization, where
p is the number of predictors in the training data, specified as
"sqeuclidean", "cityblock",
"cosine", or "correlation". The
incrementalDynamicKMeans function does not support the Hamming distance
metric. This argument sets the Distance property.
incrementalDynamicKMeans computes centroid clusters differently for the
supported distance metrics. This table summarizes the available distance metrics. In
each formula, x is an observation (that is, a row of
X) and c is a centroid (a row
vector).
| Distance Metric | Description | Formula |
|---|---|---|
"sqeuclidean" | Squared Euclidean distance (default). Each centroid is the mean of the points in the cluster. |
|
"cityblock" | Sum of absolute differences, that is, the L1 distance. Each centroid is the component-wise median of the points in the cluster. |
|
"cosine" | One minus the cosine of the included angle between points (treated as vectors). Each centroid is the mean of the points in the cluster, after the points are normalized to unit Euclidean length. |
|
"correlation" | One minus the sample correlation between points (treated as sequences of values). Each centroid is the component-wise mean of the points in the cluster, after the points are centered and normalized to zero mean and unit standard deviation. |
where
|
Example: Distance="cityblock"
Data Types: char | string
Forgetting factor for cluster centroid updates, specified as a scalar value from
0 to 1. This argument sets the ForgettingFactor
property.
A forgetting factor value of 0.1 gives more weight to the older
data than a forgetting factor value of 0.9. A forgetting factor value
of 0 indicates infinite memory, where all the previous observations
have equal weight when the incremental fit function updates the
cluster centroids.
Example: ForgettingFactor=0.1
Data Types: double | single
Number of observations to which the model must be fit before it is warm, specified as a
nonnegative integer. This argument sets the WarmupPeriod property.
When a model is warm, the incremental fit function returns
cluster indices, and the incremental updateMetrics function returns
performance metrics. When processing observations during the warm-up period, the
software ignores observations that contain at least one missing value. If you specify
C and ClusterCounts when you create
Mdl, and C contains no duplicate rows, then
IsWarm is
true and the default value of WarmupPeriod
is 0. Otherwise, the default value of
WarmupPeriod is 1000.
Note
IsWarm cannot be true if
Centroids contains any NaN values or
NumPredictors is 0.
Example: WarmupPeriod=100
Data Types: single | double
Performance metrics to track during incremental learning, specified as
"SimplifiedSilhouette". The Metrics
and DynamicMetrics properties of Mdl store two forms
of each performance metric as variables (columns) of a table,
Cumulative and Window, with individual
metrics in rows. MetricsWindowSize determines the update
frequency of the Window metrics. For more details, see Estimation Period and Simplified Silhouette.
Example: Metrics="SimplifiedSilhouette"
Data Types: char | string
Number of observations to use to compute window performance metrics, specified
as a positive integer. The default value is 200. This argument
sets the MetricsWindowSize property.
For more details on performance metrics options, see Performance Metrics.
Example: MetricsWindowSize=100
Data Types: single | double
Flag to standardize the predictor data, specified as a numeric or logical 0
(false) or 1 (true).
If you specify StandardizeData=true, the incremental
fit function estimates the predictor means
Mu and standard deviations Sigma during the
estimation period specified by EstimationPeriod, and standardizes
the predictor data.
You cannot specify StandardizeData if you specify C.
For more information, see Standardize Data.
Example: StandardizeData=true
Data Types: single | double | logical
Number of observations processed by the incremental model to estimate the predictor
means and standard deviations, specified as a nonnegative integer. This argument sets
the EstimationPeriod
property.
If you specify StandardizeData=true, the
default value is 1000. Otherwise, the default value is
0.
If you specify EstimationPeriod when you create
Mdl:
The software sets
EstimationPeriod=0when you specifyCorStandardizeData=false.The software uses
EstimationPeriodobservations to estimate the predictor means (Mu) and standard deviations (Sigma) prior to training the model.The software ignores observations that contain at least one missing value when processing observations during the estimation period.
For more details, see Estimation Period.
Example: EstimationPeriod=500
Data Types: single | double
Cluster growth penalty factor, specified as a positive scalar. The incremental
fit function uses the value of
GrowthPenaltyFactor to determine whether to add new cluster
centroids to Mdl. A higher value of
GrowthPenaltyFactor imposes a higher cost on new
centroids.
Example: GrowthPenaltyFactor=10
Data Types: single | double
Number of additional clusters, specified as a nonnegative scalar. When
MergeClusters is false (the default), the
software uses NumAdditionalClusters to set the initial values of
NumClusters and NumDynamicClusters. When
MergeClusters is true, the software uses
NumAdditionalClusters to set the initial value of
NumDynamicClusters. For more information, see the k and C input argument descriptions.
Example: NumAdditionalClusters=10
Data Types: single | double
Maximum number of clusters, specified as a positive scalar.
MaxNumClusters must be larger than
NumClusters + NumAdditionalClusters. When
the incremental fit function updates the number of clusters in
Mdl, the software ensures that
NumDynamicClusters does not exceed
MaxNumClusters.
Example: MaxNumClusters=15
Data Types: single | double
Flag indicating whether to enable cluster merging, specified as a numeric or
logical 0 (false) or 1
(true).
If you specify MergeClusters=false (the default):
NumClustersandNumDynamicClustershave the same value, which is updated when you call the incrementalfitfunction.CentroidsandDynamicCentroidshave the same value.ClusterCountsandDynamicClusterCountshave the same value.MetricsandDynamicMetricshave the same value.
If you specify MergeClusters=true:
The value of
NumClustersdoes not change after object creation.The value of
NumDynamicClustersis updated when you call the incrementalfitfunction.Centroids,ClusterCounts, andMetricscontain the values for the merged cluster centroids.
Example: MergeClusters=true
Data Types: single | double | logical
Properties
Training Parameters
This property is read-only.
Predictor means, represented as a numeric vector.
When you create
Mdland specifyNumPredictors=0orStandardizeData=false(the default), thenMuis an empty array[].When you create
Mdland setStandardizeData=true, specifyNumPredictorsas a positive integer, and specifyk, thenMuis initially a 1-by-NumPredictorsvector of zeros. Otherwise,Muis[].When you create
Mdland setStandardizeData=true, andMuis[]or an array of zeros, then the incrementalfitfunction calculates the predictor variable means using all data points that do not have any missing values. At the end of the estimation period specified byEstimationPeriod,Muis aNumPredictors-by-1 vector that contains the predictor means.
You cannot specify Mu directly.
Data Types: single | double
This property is read-only.
Predictor standard deviations, represented as a numeric vector.
When you create
Mdland specifyNumPredictors=0orStandardizeData=false(the default), thenSigmais an empty array[].When you create
Mdland setStandardizeData=true, specifyNumPredictorsas a positive integer, and specifyk, thenSigmais initially a 1-by-NumPredictorsvector of zeros. Otherwise,Sigmais[].When you create
Mdland setStandardizeData=true, andSigmais[]or an array of zeros, then the incrementalfitfunction calculates the predictor variable standard deviations using all data points that do not have any missing values. At the end of the estimation period specified byEstimationPeriod,Sigmais aNumPredictors-by-1 vector that contains the predictor standard deviations.
You cannot specify Sigma directly.
Data Types: single | double
This property is read-only after object creation.
Number of observations processed by the incremental model to estimate the predictor
means and standard deviations, represented as a nonnegative integer. If you specify
StandardizeData=true when you create
Mdl, the default value is 1000. Otherwise,
the default value is 0.
If EstimationPeriod
>
0:
The software uses
EstimationPeriodobservations to estimate the predictor means (Mu) and standard deviations (Sigma) prior to training the model.The software ignores observations that contain at least one missing value when processing observations during the estimation period.
For more details, see Estimation Period.
Data Types: single | double
This property is read-only after object creation.
Distance metric in p-dimensional space used for minimization, where
p is the number of variables in the training data, stored as
"sqeuclidean", "cityblock",
"cosine", or "correlation". For a description
of the supported distance metrics, see Distance. The incrementalDynamicKMeans function does not support
the Hamming distance metric.
Data Types: string
This property is read-only after object creation.
Forgetting factor for cluster centroid updates, represented as a scalar value
from 0 to 1. A forgetting factor value
of 0.1 gives more weight to the older data than a
forgetting factor value of 0.9. A forgetting factor value
of 0 indicates infinite memory, where all the previous
observations have equal weight when the incremental fit
function updates the cluster centroids.
Data Types: single | double
This property is read-only.
Number of observations fit to the incremental model Mdl, represented as a
nonnegative numeric scalar. NumTrainingObservations increases when
you pass Mdl and training data to the incremental
fit function outside of the estimation period. The software
resets NumTrainingObservations to 0 when you call
the reset function.
When fitting the model, the software ignores observations that contain at least one missing value.
You cannot specify NumTrainingObservations directly.
Data Types: double
Clustering Parameters
This property is read-only after object creation.
Number of predictors, represented as a nonnegative integer.
If you specify
Cwhen you createMdland do not specifyNumPredictors, or specifyNumPredictors=0NumPredictors=size(.C,2)If you specify
kwhen you createMdland do not specifyNumPredictors, the initial value ofNumPredictorsis0.If
NumPredictors=0, the software infers the number of predictors from the training data and updatesNumPredictorswhen you call the incrementalfitfunction.
Data Types: single | double
This property is read-only after object creation.
Number of clusters, represented as a positive integer. The software updates this
property when you call the reset function or the incremental
fit function. If MergeClusters is false, then
NumClusters has the same value as
NumDynamicClusters. If MergeClusters is
true, the value of NumClusters does not
change after object creation.
Data Types: single | double
This property is read-only after object creation.
Cluster centroids, represented as a
NumClusters-by-NumPredictors numeric matrix
where each row contains a cluster centroid, and each column contains the predictor
values. The software updates this property when you call the
reset function or the incremental fit
function. If MergeClusters is false, then
Centroids and DynamicCentroids have the
same values.
Data Types: single | double
This property is read-only after object creation.
Cluster counts, represented as a
NumClusters-by-1 vector of numeric scalars.
The software updates this property when you call the reset
function or the incremental fit function. The incremental
fit function uses ClusterCounts to
determine the learning rate when it updates the cluster centroids.
If MergeClusters is false,
ClusterCounts and DynamicClusterCounts
have the same values If ForgettingFactor is 0, then each value of
ClusterCounts is 1 + the number of
observations assigned to each cluster. Otherwise, the values of
ClusterCounts represent the relative size of each
cluster.
Data Types: single | double
Dynamic Clustering Parameters
This property is read-only after object creation.
Flag indicating whether to enable cluster merging, represented as a numeric or
logical 0 (false) or 1
(true). For more information, see MergeClusters.
Data Types: logical
This property is read-only after object creation.
Number of additional clusters, specified as a nonnegative scalar. When
MergeClusters is false (the default), the
software uses NumAdditionalClusters to set the initial values of
NumClusters and NumDynamicClusters. When
MergeClusters is true, the software uses
NumAdditionalClusters to set the initial value of
NumDynamicClusters. For more information, see the k
and C
input argument descriptions.
Data Types: single | double
This property is read-only after object creation.
Maximum number of clusters, represented as a positive scalar. When the incremental
fit function updates the number of clusters in
Mdl, the software ensures that
NumDynamicClusters does not exceed
MaxNumClusters.
Data Types: single | double
This property is read-only after object creation.
Cluster growth penalty factor, represented as a positive scalar. The incremental
fit function uses the value of
GrowthPenaltyFactor to determine whether to add new cluster
centroids to Mdl. A higher value of
GrowthPenaltyFactor imposes a higher cost on new
centroids.
Data Types: single | double
This property is read-only.
Number of dynamic clusters, represented as a positive integer. If MergeClusters is false, then
NumDynamicClusters has the same value as
NumClusters.
You cannot specify NumDynamicClusters directly.
Data Types: single | double
This property is read-only.
Dynamic cluster centroids, represented as a
NumDynamicClusters-by-NumPredictors numeric
matrix, where each row contains a dynamic cluster centroid, and each column contains
the predictor values. The software updates DynamicCentroids when
you call the reset function or the incremental
fit function. If MergeClusters is false, then
DynamicCentroids and Centroids have the
same values.
You cannot specify DynamicCentroids directly.
Data Types: single | double
This property is read-only.
Dynamic cluster counts, represented as a
NumDynamicClusters-by-1 vector of numeric
scalars. The software updates DynamicClusterCounts when you call
the reset function or the incremental fit
function. The incremental fit function uses
DynamicClusterCounts to determine the learning rate when it
updates the dynamic cluster centroids.
If ForgettingFactor is 0, then each value of
DynamicClusterCounts is 1 + the number of
observations assigned to each dynamic cluster. Otherwise, the values of
DynamicClusterCounts represent the relative size of each dynamic
cluster. If MergeClusters is false,
DynamicClusterCounts and ClusterCounts have
the same values.
You cannot specify DynamicClusterCounts directly.
Data Types: single | double
Performance Metrics Parameters
This property is read-only.
Flag indicating whether the incremental fit function returns cluster
indices and the incremental updateMetrics function returns
performance metrics, represented as a numeric or logical 0
(false) or 1 (true).
IsWarm becomes true after the incremental fit function fits the incremental model to WarmupPeriod observations. However, IsWarm cannot be true if Centroids contains any NaN values or NumPredictors is 0.
If IsWarm is false:
The
idxoutput offitconsists ofNaNvalues.The
updateMetricsfunction storesNaNvalues inMetrics.
If Mdl.EstimationPeriod > 0, then during the estimation period:
IsWarmisfalse.The value of
NumTrainingObservationsis0.The
fitfunction does not fit the model.The
updateMetricsfunction does not store any values inMetrics.
You cannot specify IsWarm directly.
Data Types: single | double | logical
This property is read-only after object creation.
Number of observations to which the model must be fit before it is warm, represented
as a nonnegative integer. When a model is warm, the incremental fit
function returns cluster indices, and the incremental updateMetrics
function returns performance metrics. When processing observations during the warm-up
period, the software ignores observations that contain at least one missing value. If
you specify both C and ClusterCounts when you
create Mdl, and C contains no duplicate rows,
then IsWarm=true and the default value of
WarmupPeriod is 0. Otherwise, the default
value of WarmupPeriod is 1000.
Note
IsWarm cannot be true if
Centroids contains any NaN values or
NumPredictors is 0.
Data Types: single | double
This property is read-only.
Model performance metrics updated during incremental learning by
updateMetrics, represented as a table with two columns labeled
Cumulative and Window.
Cumulative— Model performance, as measured by the Simplified Silhouette metric, from the time the model becomes warm (IsWarmis1).Window— Model performance, as measured by the Simplified Silhouette metric, evaluated over all observations within the window specified by theMetricsWindowSizeproperty. The software updatesWindowafter it processesMetricsWindowSizeobservations.
The software sets Metrics to NaN when you
call the reset function.
You cannot specify the Metrics property
directly.
Data Types: table
This property is read-only.
Dynamic model performance metrics updated during incremental learning by
updateMetrics, represented as a table with two columns. The
software uses the dynamic clusters to calculate DynamicMetrics.
If MergeClusters=false, then
DynamicMetrics and Metrics have the same
value. The software sets DynamicMetrics to NaN
when you call the reset function. For more details, see Metrics.
Data Types: table
This property is read-only after object creation.
Number of observations to use to compute window performance metrics, represented as a positive integer. The default value is 200.
For more details on performance metrics options, see Performance Metrics.
Data Types: single | double
Object Functions
fit | Train model for incremental dynamic k-means clustering |
updateMetrics | Update performance metrics in incremental dynamic k-means clustering model given new data |
assignClusters | Assign observations to existing clusters and dynamic clusters |
reset | Reset incremental dynamic k-means clustering model |
Examples
Create a training data set of 10,000 observations of three predictors. The data set contains ten groups of 1000 observations each. The predictor values of each group centroid lie within the range ([–10,10], [–10,10], [–10,10]). Store the group identification numbers in ids.
rng(0,"twister"); % For reproducibility ngroups = 10; obspergroup = 1000; Xtrain = []; ids = []; cposrange = 10; for c = 1:ngroups sigma = rand; Xtrain = [Xtrain; randn(obspergroup,3)*sigma + ... (randi(2*cposrange,[1,3])-cposrange).*ones(obspergroup,3)]; ids = [ids; c*ones(obspergroup,1)]; end
Shuffle the data set.
ntrain = size(Xtrain,1); indices = randperm(ntrain); Xtrain = Xtrain(indices,:); ids = ids(indices,:);
Split off the last 2000 observations to create a test set.
Xtest = Xtrain(end-1999:end,:); idsTest = ids(end-1999:end,:); Xtrain = Xtrain(1:end-2000,:); ids = ids(1:end-2000,:);
Plot the data set and color the observations according to their group number.
scatter3(Xtrain(:,1),Xtrain(:,2),Xtrain(:,3),1,ids,"filled");
colormap(jet);
Create Incremental Model
Create an incremental dynamic k-means model object with numClusters=2 and default parameters.
Mdl = incrementalDynamicKMeans(numClusters=2);
Display the initial number of clusters and dynamic clusters.
Mdl.NumClusters
ans = 11
Mdl.NumDynamicClusters
ans = 11
The software sets Mdl.NumClusters using the specified value of NumClusters and the default value of NumAdditionalClusters (10). Because the default value of MergeClusters is false, the cluster and dynamic cluster property values of Mdl are identical.
Fit Incremental Clustering Model
Fit the incremental dynamic clustering model to the data using the fit function. To simulate a data stream, fit the model in chunks of 50 observations at a time. Because default value of WarmupPeriod is 1000, updateMetrics only updates performance metrics after the 20th iteration. At each iteration:
Process 50 observations.
Store the number of clusters in
numClustersto see how it evolves during incremental learning.Overwrite the previous incremental model with a new one fitted to the incoming observations.
Update the window and cumulative simplified silhouette performance metrics using the
updateMetricsfunction.Store the metrics for the merged clusters in
silto see how they evolve during incremental learning.
numObsPerChunk = 50; n = size(Xtrain,1); nchunk = floor(n/numObsPerChunk); sil = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]); numClusters = zeros(nchunk); for j = 1:nchunk numClusters(j) = Mdl.NumClusters; ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); chunkrows = ibegin:iend; Mdl = fit(Mdl,Xtrain(chunkrows,:)); Mdl = updateMetrics(Mdl,Xtrain(chunkrows,:)); sil{j,:} = Mdl.Metrics{'SimplifiedSilhouette',:}; end
Analyze Incremental Model During Training
Plot the number of clusters at the start of each iteration.
plot(numClusters) xlabel("Iteration") ylabel("Number of Clusters")

The model initially has 11 clusters, and has 14 clusters at the final iteration.
figure; plot(sil.Variables); xlim([0 nchunk]) ylabel("Simplified Silhouette") xline(Mdl.WarmupPeriod/numObsPerChunk,"g-.") legend(sil.Properties.VariableNames,Location="southeast") xlabel("Iteration")

The plot indicates that when the model becomes warm, the window performance metric value is 0.83. After the 90th iteration, the metric value steadily increases.
Create a bar chart of the cluster counts after the final iteration.
bar(Mdl.ClusterCounts)
xlabel("Cluster")
The plot shows that the observations are distributed relatively equally among all clusters except clusters 2, 5, 6, 7, and 13.
Plot the test data set and color the points according to the cluster assignments of the final trained model. Plot the fitted cluster centroids using blue pentagram markers.
idx = assignClusters(Mdl,Xtest); scatter3(Xtest(:,1),Xtest(:,2),Xtest(:,3),5,idx,"filled"); colormap(jet) hold on C = Mdl.Centroids; scatter3(C(:,1),C(:,2),C(:,3),100,"b","Pentagram","filled"); hold off

The plot shows that some groups in the test set are fit by a single cluster, while others are fit by two clusters.
Create a data set with 20,000 observations of three predictors. The data set contains two groups of 10,000 observations each. Store the group identification numbers in ids.
rng(0,"twister"); % For reproducibility ngroups = 2; obspergroup = 10000; Xtrain = []; ids = []; sigma = 0.4; for c = 1:ngroups Xtrain = [Xtrain; randn(obspergroup,3)*sigma + ... (randi(2,[1,3])-1).*ones(obspergroup,3)]; ids = [ids; c*ones(obspergroup,1)]; end
Shuffle the data set.
ntrain = size(Xtrain,1); indices = randperm(ntrain); Xtrain = Xtrain(indices,:); ids = ids(indices,:);
Create a test set that contains the last 2000 observations of the data set. Store the group identification numbers for the test set in idsTest. Keep the first 18,000 observations as the training set.
Xtest = Xtrain(end-1999:end,:); idsTest = ids(end-1999:end,:); Xtrain = Xtrain(1:end-2000,:); ids = ids(1:end-2000,:);
Plot the training set, and color the observations according to their group identification number.
scatter3(Xtrain(:,1),Xtrain(:,2),Xtrain(:,3),1,ids,"filled");
Create Incremental Model
Create an incremental dynamic k-means model object with a warm-up period of 1000 observations. Specify that the incremental fit function stores two clusters that are merged from the dynamic clusters.
Mdl = incrementalDynamicKMeans(numClusters=2, ...
WarmupPeriod=1000, MergeClusters=true)Mdl =
incrementalDynamicKMeans
IsWarm: 0
Metrics: [1×2 table]
NumClusters: 2
NumDynamicClusters: 11
Centroids: [2×0 double]
DynamicCentroids: [11×0 double]
Distance: "sqeuclidean"
Properties, Methods
Mdl is an incrementalDynamicKMeans model object that is prepared for incremental learning.
Fit Incremental Clustering Model
Fit the incremental clustering model Mdl to the data using the fit function. To simulate a data stream, fit the model in chunks of 100 observations at a time. Because WarmupPeriod = 1000, fit only returns cluster indices after the tenth iteration. At each iteration:
Process 100 observations.
Store the number of dynamic clusters in
numDynClusters, to see how it evolves during incremental learning.Overwrite the previous incremental model with a new one fitted to the incoming observations.
Update the simplified silhouette performance metrics (
CumulativeandWindow) using theupdateMetricsfunction.Store the metrics for the merged clusters in
siland the metrics for the dynamic clusters indynsil, to see how they evolve during incremental learning.
numObsPerChunk = 100; n = size(Xtrain,1); nchunk = floor(n/numObsPerChunk); sil = array2table(zeros(nchunk,2),"VariableNames",["Cumulative" "Window"]); dynsil = array2table(zeros(nchunk,2),"VariableNames",["Cumulative" "Window"]); numDynClusters = []; for j = 1:nchunk numDynClusters(j) = Mdl.NumDynamicClusters; ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); chunkrows = ibegin:iend; Mdl = fit(Mdl,Xtrain(chunkrows,:)); Mdl = updateMetrics(Mdl,Xtrain(chunkrows,:)); sil{j,:} = Mdl.Metrics{"SimplifiedSilhouette",:}; dynsil{j,:} = Mdl.DynamicMetrics{"SimplifiedSilhouette",:}; end
Analyze Incremental Model During Training
Plot the number of dynamic clusters at the start of each iteration.
plot(numDynClusters)
xlabel("Iteration");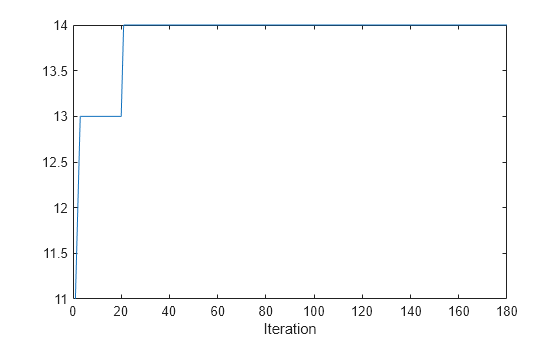
The model initially has 11 dynamic clusters, and 14 dynamic clusters at the final iteration.
Plot the mean simplified silhouette metric for the merged clusters and the dynamic clusters.
figure; t = tiledlayout(2,1); nexttile h = plot(sil.Variables); ylabel("Simplified Silhouette") xline(Mdl.WarmupPeriod/numObsPerChunk,"b:") legend(h,sil.Properties.VariableNames,Location="southeast") title("Merged Cluster Metrics") nexttile h2 = plot(dynsil.Variables); ylabel("Simplified Silhouette") xline(Mdl.WarmupPeriod/numObsPerChunk,"b:") legend(h2,dynsil.Properties.VariableNames,Location="northeast") xlabel(t,"Iteration") title("Dynamic Cluster Metrics")
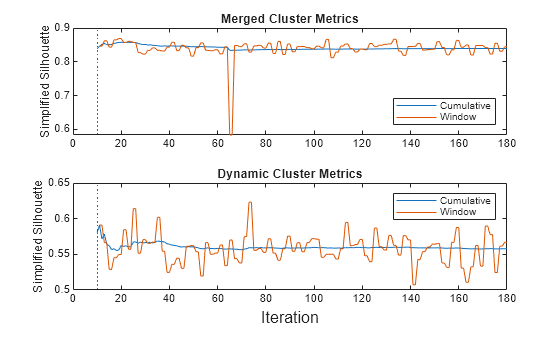
After the warm-up period, the updateMetrics function returns performance metrics. A high metric value indicates that, on average, each observation is well matched to its own cluster and poorly matched to other clusters. The higher metric values in the top plot indicate that the merged clusters provide a better clustering solution for the data than the unmerged dynamic clusters.
Analyze the Final Clustering Model Using the Test Set
Create a bar chart of the dynamic cluster counts after the final iteration.
figure
bar(Mdl.DynamicClusterCounts)
xlabel("Dynamic Cluster Number");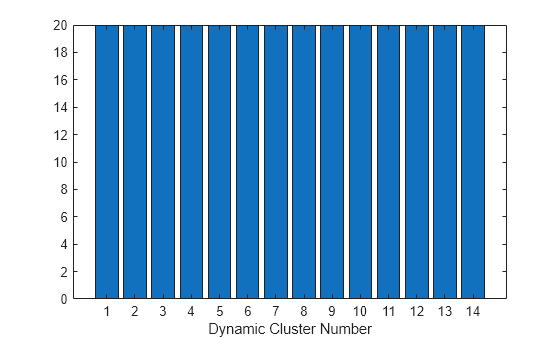
The bar chart shows that the model assigns the observations equally among the dynamic clusters.
Plot the test data set, and color the points according to the dynamic cluster assignments of the final trained model. Plot the dynamic cluster centroids using blue pentagram markers.
C = Mdl.DynamicCentroids; [~,~,dynIdx] = assignClusters(Mdl,Xtest); figure; scatter3(Xtest(:,1),Xtest(:,2),Xtest(:,3),3,dynIdx,"filled"); hold on scatter3(C(:,1),C(:,2),C(:,3),100,"b","Pentagram","filled"); hold off

The dynamic cluster centroids are located within the overall distribution of the observations, and are equally divided among the two groups in the data.
Plot the test data set and color the points according to the merged cluster assignments of the final trained model. Use the color red for the observations whose merged cluster assignments do not match the group identification numbers. Plot the merged cluster centroids using blue pentagram markers.
C = Mdl.Centroids; idx = assignClusters(Mdl,Xtest); incorrectIds = find(idx ~= idsTest); figure; scatter3(Xtest(:,1),Xtest(:,2),Xtest(:,3),1,idx,"filled"); hold on scatter3(C(:,1),C(:,2),C(:,3),100,"b","Pentagram","filled"); scatter3(Xtest(incorrectIds,1),Xtest(incorrectIds,2),Xtest(incorrectIds,3),5,"r","filled") hold off
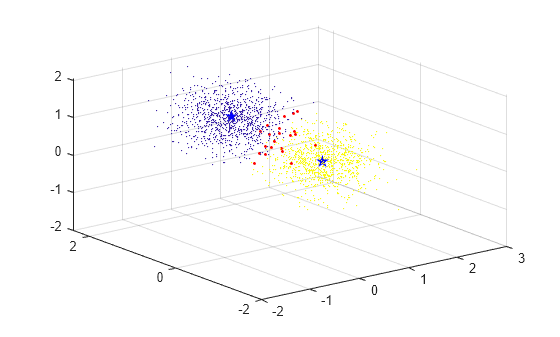
The plot shows that the merged centroids lie near the center of each group in the data. The observations with incorrect cluster assignments lie mainly in the region in between the two groups.
Use the helper function AdjustedRandIndex to calculate the adjusted Rand index, which measures the similarity of the clustering indices and the group identification numbers.
AdjustedRandIndex(idx,idsTest)
ans = 0.9584
The adjusted Rand index is close to 1, indicating that the clustering model does a good job of correctly predicting the group identification numbers of the test set observations.
function ARI = AdjustedRandIndex(labels1, labels2) % Helper function to calculate the Adjusted Rand Index (ARI) to % measure the similarity between two clustering labels labels1 % and labels2. C = confusionmat(labels1, labels2); n = numel(labels2); % Calculate sums for rows and columns sumRows = sum(C, 2); sumCols = sum(C, 1); ss = sum(C.^2,"all"); TN = ss-n; % True negatives FP = sum(C*sumCols')-ss; % False positives FN = sum(C'*sumRows)-ss; % False negatives TP = n^2-FP-FN-ss; % True positives if FN == 0 && FP == 0 ARI = 1; else ARI = 2*(TP*TN-FN*FP)/((TP+FN)*(FN+TN)+(TP+FP)*(FP+TN)); end end % LocalWords: ARI
Prepare an incremental dynamic k-means model by specifying two initial clusters and enable the merging of dynamic clusters. The software uses the specified value of NumAdditionalClusters to set an initial number of dynamic clusters. Specify a growth penalty factor of 500, which imposes a higher cost when the incremental fit function adds more dynamic clusters. Also specify a warm-up period of 100 observations.
Mdl = incrementalDynamicKMeans(numClusters=2,MergeClusters=true, ...
NumAdditionalClusters=1,GrowthPenaltyFactor=500,WarmupPeriod=100)Mdl =
incrementalDynamicKMeans
IsWarm: 0
Metrics: [1×2 table]
NumClusters: 2
NumDynamicClusters: 2
Centroids: [2×0 double]
DynamicCentroids: [2×0 double]
Distance: "sqeuclidean"
Properties, Methods
Mdl is an incrementalDynamicKMeans model object that is configured for incremental learning. The model initially has two dynamic clusters, and two clusters that are merged from the dynamic clusters.
Load and Sort Data
Load the humanactivity.mat file.
load humanactivity.matThis data set contains 20,000 observations of five physical human activities: Sitting (1), Standing (2), Walking (3), Running (4), and Dancing (5). Each observation has 60 features extracted from acceleration data measured by smartphone accelerometer sensors.
Sort the data set so that the first 5000 observations contain only activity modes 1 and 2, the next 5000 observations contain activity modes 1, 2, and 3, and so on.
rng(0,"twister"); % For reproducibility selectID12 = find(actid == 1 | actid == 2); selectID123 = find(actid == 1 | actid == 2 | actid == 3); selectID1234 = find(actid == 1 | actid == 2 | actid == 3 | actid == 4); batch2 = selectID12(randperm(length(selectID12),5000)); batch3 = selectID123(randperm(length(selectID123),5000)); batch4 = selectID1234(randperm(length(selectID1234),5000)); batch5 = randperm(length(actid),5000)'; feat = [feat(batch2,:); feat(batch3,:); feat(batch4,:); feat(batch5,:)]; actid = [actid(batch2); actid(batch3); actid(batch4); actid(batch5)];
Fit Incremental Clustering Model
Fit the incremental clustering model Mdl to the data by using the fit function. To simulate a data stream, fit the model in chunks of 100 observations at a time. Because WarmupPeriod = 100, fit only returns cluster indices after the first iteration. At each iteration:
Process 100 observations.
Overwrite the previous incremental model with a new one fitted to the incoming observations.
Return the dynamic cluster indices for the data chunk.
Store
actIDcounts, a matrix that contains the number of observations of each activity mode (columns) assigned to each dynamic cluster (rows), to see how it evolves during incremental learning.Store the simplified silhouette performance metrics (
CumulativeandWindow) insilDynamic, to see how they evolve during incremental learning.
n = numel(feat(:,1)); numObsPerChunk = 100; nchunk = floor(n/numObsPerChunk); numIDs = numel(unique(actid)); % Number of unique activity modes actIDcounts = zeros(10,numIDs,nchunk); silDynamic = array2table(zeros(nchunk,2), ... VariableNames=["Cumulative" "Window"]); % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1); iend = min(n,numObsPerChunk*j); chunkrows = ibegin:iend; [Mdl,~,dynamicIndices] = fit(Mdl,feat(chunkrows,:)); ids = [dynamicIndices,actid(chunkrows)]; Mdl = updateMetrics(Mdl,feat(chunkrows,:)); silDynamic{j,:} = Mdl.DynamicMetrics{'SimplifiedSilhouette',:}; for k = 1:Mdl.NumDynamicClusters for i = 1:numIDs actIDcounts(k,i,j) = sum(ids(:,1)==k & ids(:,2)==i); end end end
Display the number of merged clusters and dynamic clusters in the model after the final iteration.
Mdl.NumClusters
ans = 2
Mdl.NumDynamicClusters
ans = 5
The final model contains 2 merged clusters and 5 dynamic clusters.
For each dynamic cluster, plot the number of observations belonging to each of the five activity modes to see how they evolve during incremental learning.
figure t = tiledlayout(Mdl.NumDynamicClusters,1,TileSpacing="none"); for c = 1:Mdl.NumDynamicClusters nexttile plot(squeeze(actIDcounts(c,:,:))') xticks(10:10:190); yticks([15 30 45]); xline(5001/numObsPerChunk,"b:") xline(10001/numObsPerChunk,"b:") xline(15001/numObsPerChunk,"b:") yLimits = ylim; ylabel("N_{obs}"); text(155,yLimits(2)-0.2*diff(yLimits), ... sprintf("Dynamic Cluster %d",c),FontSize=8); end legend("ActID 1","ActID 2","ActID 3","ActID 4","ActID 5",location="west") xlabel("Iteration")
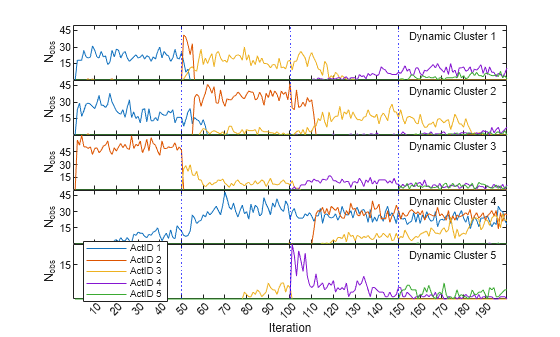
The vertical dotted lines in the plot indicate the iteration number at which a new activity mode appears in the streaming data. Each colored line represents a different activity mode. Only two activity modes are present prior to iteration 50. Observations corresponding to activity mode 1 are split between dynamic clusters 1 and 2, while all the activity mode 2 observations are assigned to cluster 3. As more activity mode observations are introduced during iterations 50 through 200, the algorithm allocates them more evenly among all the dynamic clusters. After the final iteration, activity modes 1, 2, and 3 (sitting, standing, and walking) are all assigned to cluster 4, while activity modes 4 and 5 (running and dancing) are distributed equally among the other clusters.
Plot the simplified silhouette metric for the dynamic clusters to see how it evolves over time. A high metric value indicates that, on average, each observation is well matched to its own cluster and poorly matched to other clusters.
figure plot(silDynamic.Variables); xline(5001/numObsPerChunk,"b:") xline(10001/numObsPerChunk,"b:") xline(15001/numObsPerChunk,"b:") xlabel("Iteration") ylabel("Simplified Silhouette") xline(Mdl.WarmupPeriod/numObsPerChunk,'g-.') legend(silDynamic.Properties.VariableNames,Location="southeast")
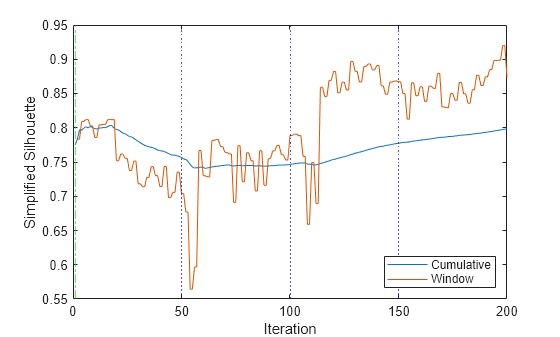
The window metric value is relatively constant for the first 50 iterations, and then drops slightly between iterations 50 and 113. The metric value jumps significantly at iteration 114, when the algorithm assigns all the activity mode 2 observations to dynamic cluster 4. The final metric value is close to the maximum possible value of 1.
More About
The k-means clustering algorithm [2] is a data-partitioning algorithm that assigns observations (points) to exactly
one of k clusters defined by centroids, where
k is specified before the algorithm starts. The
incremental k-means fit function uses a
gradient descent method based on the algorithm in [3] to minimize the sum
of point-to-centroid distances, summed over all k
clusters.
The incremental dynamic k-means clustering algorithm of [1] was developed for streaming data. After receiving each batch of data, the algorithm can create new cluster centroids in order to obtain a better clustering solution, according to a specified distance metric and growth penalty factor. This factor imposes an additional cost as the number of dynamic clusters increases.
Here, the term cluster refers to a dynamic cluster that the
software stores in the incrementalDynamicKMeans model object
Mdl. When Mdl.MergeClusters is
true, Mdl contains the property values
of an additional fixed number of clusters that are merged from the dynamic
clusters.
When you call fit with an
incrementalDynamicKMeans model object
Mdl and a batch of data X:
If
Mdlhas i missing centroid locations, the function sets their locations equal to the first i unique observations inX.The function finds cluster indices for all the observations in
Xusing the current centroid locations. The cluster index of each observation corresponds to the closest cluster centroid according to the distance metric inMdl.The function determines whether to add any new clusters and update
NumDynamicClusters, based on the point-to-centroid distances and the growth penalty factor.The function updates the p cluster centroids
DynamicCentroidsusing the following steps:Compute gradients using the distance between each observation and the centroid p.
Update the
DynamicClusterCountsvalueCCpfor cluster p using the formulaCCp,new=(1-ForgettingFactor)*CCp+Cp, whereCpis the number of observations inXthat have cluster index p according to the current model.Use 1/
CCp,newas the learning rate for the gradient descent update.Update the cluster centroid p by looping over each observation with cluster index p, using the computed gradient for each observation.
If
Mdl.MergeClustersistrue, the function updatesMdl.CentroidsandMdl.ClusterCountswith merged dynamic cluster values. Otherwise, the function setsMdl.Centroids,Mdl.ClusterCounts, andMdl.NumClustersto the corresponding dynamic cluster property values.
The updateMetrics
function tracks model performance metrics (Metrics and
DynamicMetrics) from new data when the incremental dynamic model is
warm (Mdl.IsWarm property). An incremental dynamic model becomes warm
after fit fits the
incremental dynamic model to WarmupPeriod observations, which is the
warm-up period.
If Mdl.EstimationPeriod > 0, the software estimates the predictor
means and standard deviations before fitting the model to data. Therefore, the software must
process an additional EstimationPeriod observations before the model
starts the warm-up period.
The Metrics property of the incremental dynamic model stores two
forms of each performance metric as variables (columns) of a table,
Cumulative and Window, with individual metrics in
rows. When the incremental dynamic model is warm, updateMetrics updates
the metrics at the following frequencies:
Cumulative— The function computes cumulative metrics since the start of model performance tracking. The function updates metrics every time you call it, and bases the calculation on the entire supplied data set until a model reset.Window— The function computes metrics based on all observations within a window determined by theMetricsWindowSizename-value argument.MetricsWindowSizealso determines the frequency at which the software updatesWindowmetrics. For example, ifMetricsWindowSizeis 20, the function computes metrics based on the last 20 observations in the supplied data (X((end – 20 + 1):end,:)andY((end – 20 + 1):end)).Incremental functions that track performance metrics within a window use the following process:
Store
MetricsWindowSizeamount of values for each specified metric.Populate elements of the metrics values with the model performance based on batches of incoming observations.
When the window of observations is filled, overwrite
Mdl.Metrics.WindowandMdl.DynamicMetrics.Windowwith the average performance in the metrics window. If the window is overfilled when the function processes a batch of observations, the latest incomingMetricsWindowSizeobservations are stored, and the earliest observations are removed from the window. For example, supposeMetricsWindowSizeis 20, the window contains 10 stored values from a previously processed batch, and 15 values are incoming. To compose the length 20 window, the functions use the measurements from the 15 incoming observations and the latest 5 measurements from the previous batch.
The software omits an observation with a NaN cluster index when
computing the Cumulative and Window performance metric
values.
If incremental learning functions are configured to standardize predictor variables, they
do so using the means and standard deviations stored in the Mu and
Sigma properties, respectively, of the incremental learning model
Mdl. The incremental fit function estimates
means and standard deviations using the estimation period observations when:
You specify
StandardizeData=truewhen you createMdlMdl.EstimationPeriodis positive (see Estimation Period).Mdl.Muis[]or an array of zeros, andMdl.Sigmais[]or an array of ones.
During the estimation period, the incremental fit function does not
fit the model. The function uses the first incoming EstimationPeriod
observations to estimate the variable means and standard deviations. At the end of the
estimation period, the function updates the Mu and
Sigma properties of the model.
Estimation occurs only when:
You specify
StandardizeData=truewhen you createMdl.Mdl.EstimationPeriodis positive.Mdl.Muis[]or an array of zeros, andMdl.Sigmais[]or an array of ones.
The simplified silhouette value si for the ith point is defined as
where ap,i is the distance of
the ith point to the centroid of its cluster p[4].
bp,i is the distance of the
ith point to the centroid of its closest neighboring cluster. If the
ith point is the only point in its cluster, then the simplified
silhouette value of the point is 1.
The simplified silhouette values range from –1 to 1.
A high value indicates that the point is well matched to its own cluster and poorly matched
to other clusters. If most points have a high simplified silhouette value, then the
clustering solution is appropriate. If many points have a low or negative simplified
silhouette value, then the clustering solution might have too many or too few clusters. You
can use simplified silhouette values as a clustering evaluation criterion with any distance
metric. By default, the performance metric values stored in the model object are the average
simplified silhouette values for all points passed to the updateMetrics
function.
Tips
You can create an
incrementalDynamicKMeansmodel object that incorporates the outputs of thekmeansfunction by using the following code:k = 2; [idx,C]=kmeans(X,k); countTable = tabulate(idx); counts = countTable(:,2) Mdl = incrementalDynamicKMeans(centroids=C,ClusterCounts=counts);
References
[1] Liberty, Edo, Ram Sriharsha, and Maxim Sviridenko. An Algorithm for Online K-Means Clustering. In 2016 Proceedings of the Eighteenth Workshop on Algorithm Engineering and Experiments (ALENEX), 81–89. Society for Industrial and Applied Mathematics, 2016.
[2] Lloyd, S. Least Squares Quantization in PCM. IEEE Transactions on Information Theory 28, no. 2 (March 1982): 129–37.
[3] Sculley, D. Web-Scale k-Means Clustering. In Proceedings of the 19th International Conference on World Wide Web, 1177–78. Raleigh North Carolina USA: ACM, 2010.
[4] Vendramin, Lucas, Ricardo J.G.B. Campello, and Eduardo R. Hruschka. On the Comparison of Relative Clustering Validity Criteria. In Proceedings of the 2009 SIAM international conference on data mining, 733–744. Society for Industrial and Applied Mathematics, 2009.
Version History
Introduced in R2025a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)