rangesearch
Find all neighbors within specified distance using input data
Description
Examples
Find the X points that are within a Euclidean distance 1.5 of each Y point. Both X and Y are samples of five-dimensional normally distributed variables.
rng('default') % For reproducibility X = randn(100,5); Y = randn(10,5); [Idx,D] = rangesearch(X,Y,1.5)
Idx=10×1 cell array
{[ 25 62 33 99 87 92 16]}
{[ 92 25]}
{[ 93 42 31 73 60 28 78 83 48 89 85]}
{[ 92 41]}
{[44 7 28 78 75 42 69 31 1 26 83 93]}
{[ 15 31 89 41 27 17 29 60 34]}
{[ 89]}
{1×0 double }
{1×0 double }
{1×0 double }
D=10×1 cell array
{[ 0.9546 1.0987 1.2730 1.3981 1.4140 1.4249 1.4822]}
{[ 1.4203 1.4558]}
{[ 0.7114 0.7552 1.0081 1.1324 1.1424 1.1637 1.2108 1.3824 1.3944 1.4116 1.4605]}
{[ 1.1244 1.4672]}
{[0.7863 0.9326 0.9773 1.0508 1.1722 1.1934 1.3218 1.3623 1.3869 1.3919 1.4814 1.4978]}
{[ 1.2824 1.2843 1.3342 1.3469 1.4154 1.4237 1.4625 1.4626 1.4744]}
{[ 1.1739]}
{1×0 double }
{1×0 double }
{1×0 double }
In this case, the last three Y points are more than 1.5 distance away from any X point. X(89,:) is 1.1739 distance away from Y(7,:), and no other X point is within distance 1.5 of Y(7,:). X contains 12 points within distance 1.5 of Y(5,:).
Generate 5000 random points from each of three distinct multivariate normal distributions. Shift the means of the distributions so that the randomly generated points are likely to form three separate clusters.
rng('default') % For reproducibility N = 5000; dist = 10; X = [mvnrnd([0 0],eye(2),N); mvnrnd(dist*[1 1],eye(2),N); mvnrnd(dist*[-1 -1],eye(2),N)];
For each point in X, find the points in X that are within a radius dist away from the point. For faster computation, specify to keep the indices of the nearest neighbors unsorted. Select the first point in X, and find its nearest neighbors.
Idx = rangesearch(X,X,dist,'SortIndices',false);
x = X(1,:);
nearestPoints = X(Idx{1},:);Find the values in X that are not the nearest neighbors of x. Display those points in one color and the nearest neighbors of x in a different color. Label the point x with a black, filled circle.
nonNearestIdx = true(size(X,1),1);
nonNearestIdx(Idx{1}) = false;
scatter(X(nonNearestIdx,1),X(nonNearestIdx,2))
hold on
scatter(nearestPoints(:,1),nearestPoints(:,2))
scatter(x(1),x(2),'black','filled')
hold off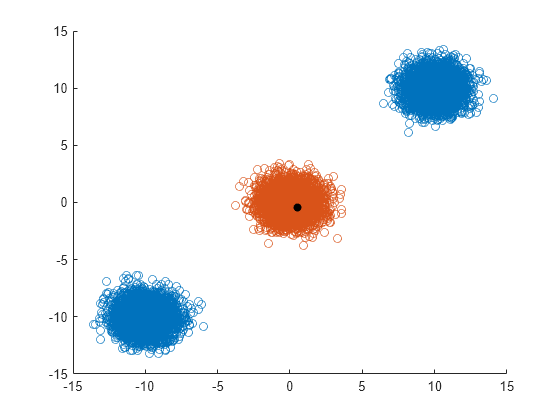
Find the patients in the patients data set that are within a certain age and weight range of the patients in Y.
Load the patients data set. The Age values are in years, and the Weight values are in pounds.
load patients X = [Age Weight]; Y = [20 162; 30 169; 40 168]; % New patients
Create a custom distance function distfun that determines the distance between patients in terms of age and weight. For example, according to distfun, two patients that are one year apart in age and have the same weight are one distance unit apart. Similarly, two patients that have the same age and are five pounds apart in weight are also one distance unit apart.
type distfun.m % Display contents of distfun.m file
function D2 = distfun(ZI,ZJ) ageDifference = abs(ZI(1)-ZJ(:,1)); weightDifference = abs(ZI(2)-ZJ(:,2)); D2 = ageDifference + 0.2*weightDifference; end
Note: If you click the button located in the upper-right section of this example and open the example in MATLAB®, then MATLAB opens the example folder. This folder includes the function file distfun.m.
Find the patients in X that are within the distance 2 of the patients in Y.
[Idx,D] = rangesearch(X,Y,2,'Distance',@distfun)Idx=3×1 cell array
{1×0 double}
{1×0 double}
{[ 41]}
D=3×1 cell array
{1×0 double}
{1×0 double}
{[ 1.8000]}
The third patient in Y is the only one to have a patient in X within a distance of 2.
Display the Age and Weight values for the nearest patient in X to the patient with age 40 and weight 168.
X(Idx{3},:)ans = 1×2
39 164
Input Arguments
Input data, specified as an mx-by-n numeric
matrix, where each row represents one n-dimensional point. The number
of columns n must equal the number of columns in
Y.
Data Types: single | double
Query points, specified as an my-by-n numeric
matrix, where each row represents one n-dimensional point. The number
of columns n must equal the number of columns in
X.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: rangesearch(X,Y,1.4,'Distance','seuclidean','Scale',iqr(X))
specifies to find all the observations in X within distance
1.4 of each observation in Y, using a standardized
Euclidean distance scaled by the interquartile range of X.
Nearest neighbor search method, specified as the comma-separated pair consisting
of 'NSMethod' and one of these values.
| Value | Description |
|---|---|
'kdtree' | Create and use a Kd-tree to find nearest
neighbors.
|
'exhaustive' | Use the exhaustive search algorithm. The software computes the distances
from all X points to each Y point to
find nearest neighbors. |
'kdtree' is the default value when the number of columns in
X is less than or equal to 10,
X is not sparse, and the distance metric is one of the valid
'kdtree' metrics. Otherwise, the default value is
'exhaustive'.
Example: 'NSMethod','exhaustive'
Distance metric that rangesearch uses, specified as the
comma-separated pair consisting of 'Distance' and one of the values
in this table.
| Value | Description |
|---|---|
'euclidean' | Euclidean distance. |
'seuclidean' | Standardized Euclidean distance. Each coordinate difference between a row
in X and a query point is scaled by dividing by the
corresponding element of the standard deviation computed from
X, std(X,'omitnan'). To specify
another scaling, use the 'Scale' name-value pair
argument. |
'mahalanobis' | Mahalanobis distance, computed using a positive definite covariance
matrix C. The default value of C is the
sample covariance matrix of X, as computed by
cov(X,'omitrows'). To specify a different value for
C, use the 'Cov' name-value pair
argument. |
'cityblock' | City block distance. |
'minkowski' | Minkowski distance. The default exponent is 2. To
specify a different exponent, use the 'P' name-value pair
argument. |
'chebychev' | Chebychev distance (maximum coordinate difference). |
'cosine' | One minus the cosine of the included angle between observations (treated as vectors). |
'correlation' | One minus the sample linear correlation between observations (treated as sequences of values). |
'hamming' | Hamming distance, the percentage of coordinates that differ. |
'jaccard' | One minus the Jaccard coefficient, the percentage of nonzero coordinates that differ. |
'spearman' | One minus the sample Spearman's rank correlation between observations (treated as sequences of values). |
@ | Custom distance function handle. A distance function has the form function D2 = distfun(ZI,ZJ) % calculation of distance ...
|
For more information, see Distance Metrics.
Example: 'Distance','minkowski'
Exponent for the Minkowski distance metric, specified as the comma-separated pair
consisting of 'P' and a positive scalar. This argument is valid
only if 'Distance' is 'minkowski'.
Example: 'P',4
Data Types: single | double
Covariance matrix for the Mahalanobis distance metric, specified as the
comma-separated pair consisting of 'Cov' and a positive definite
matrix. This argument is valid only when 'Distance' is
'mahalanobis'.
Example: 'Cov',eye(4)
Data Types: single | double
Scale parameter value for the standardized Euclidean distance metric, specified as
the comma-separated pair consisting of 'Scale' and a nonnegative
vector. Scale has length equal to the number of columns in
X. Each coordinate difference between a row in
X and a query point is scaled by the corresponding element of
Scale. This argument is valid only when
'Distance' is 'seuclidean'.
Example: 'Scale',iqr(X)
Data Types: single | double
Maximum number of data points in the leaf node of the Kd-tree,
specified as the comma-separated pair consisting of 'BucketSize'
and a positive integer scalar. This argument is valid only when
NSMethod is 'kdtree'.
Example: 'BucketSize',20
Data Types: single | double
Flag to sort returned indices according to distance, specified as the
comma-separated pair consisting of 'SortIndices' and either
true (1) or false
(0).
For faster performance when Y contains many observations that
have many nearest points in X, you can set
SortIndices to false. In this case,
rangesearch returns the indices of the nearest points in no
particular order. When SortIndices is true,
the function arranges the indices of the nearest points in ascending order by
distance.
Example: 'SortIndices',false
Data Types: logical
Output Arguments
Indices of nearest points, returned as a cell array of numeric vectors.
Idx is an my-by-1 cell
array, where my is the number of rows in Y. The
vector Idx{j} contains the indices of points (rows) in
X whose distances to Y(j,:) are not greater
than r. If SortIndices is
true, then rangesearch arranges the indices in
ascending order by distance.
Distances of the nearest points to the query points, returned as a cell array of numeric vectors.
D is an my-by-1 cell
array, where my is the number of rows in Y.
D{j} contains the distance values between Y(j,:)
and the points (rows) in X(Idx{j},:). If
SortIndices is true, then
rangesearch arranges the distances in ascending order.
Tips
For a fixed positive real value
r,rangesearchfinds all theXpoints that are within a distancerof eachYpoint. To find the k points inXthat are nearest to eachYpoint, for a fixed positive integer k, useknnsearch.rangesearchdoes not save a search object. To create a search object, usecreatens.
Algorithms
For an overview of the kd-tree algorithm, see k-Nearest Neighbor Search Using a Kd-Tree.
The exhaustive search algorithm finds the distance from each point in
Xto each point inY.
Alternative Functionality
If you set the rangesearch function 'NSMethod'
name-value pair argument to the appropriate value ('exhaustive' for an
exhaustive search algorithm or 'kdtree' for a Kd-tree
algorithm), then the search results are equivalent to the results obtained by conducting a
distance search using the rangesearch object function. Unlike the
rangesearch function, the rangesearch object function requires an ExhaustiveSearcher or KDTreeSearcher model object.
Extended Capabilities
The
rangesearch function supports tall arrays with the following usage
notes and limitations:
If
Xis a tall array, thenYcannot be a tall array. Similarly, ifYis a tall array, thenXcannot be a tall array.
For more information, see Tall Arrays.
Usage notes and limitations:
For code generation, the default value of the
'NSMethod'name-value pair argument is'exhaustive'when the number of columns inXis greater than 7.The value of the
'Distance'name-value pair argument must be a compile-time constant and cannot be a custom distance function.The
'SortIndices'name-value pair argument is not supported. The output arguments are always sorted.Names in name-value arguments must be compile-time constants. For example, to allow a user-defined exponent for the Minkowski distance in the generated code, include
{coder.Constant('Distance'),coder.Constant('Minkowski'),coder.Constant('P'),0}in the-argsvalue ofcodegen(MATLAB Coder).The sorted order of tied distances in the generated code can be different from the order in MATLAB® due to numerical precision.
When
rangesearchuses the kd-tree search algorithm, and the code generation build type is a MEX function,codegen(MATLAB Coder) generates a MEX function using Intel® Threading Building Blocks (TBB) for parallel computation. Otherwise,codegengenerates code usingparfor(MATLAB Coder).MEX function for the kd-tree search algorithm —
codegengenerates an optimized MEX function using Intel TBB for parallel computation on multicore platforms. You can use the MEX function to accelerate MATLAB algorithms. For details on Intel TBB, see https://www.intel.com/content/www/us/en/developer/tools/oneapi/onetbb.html.If you generate the MEX function to test the generated code of the
parforversion, you can disable the usage of Intel TBB. Set theExtrinsicCallsproperty of the MEX configuration object tofalse. For details, seecoder.MexCodeConfig(MATLAB Coder).MEX function for the exhaustive search algorithm and standalone C/C++ code for both algorithms — The generated code of
rangesearchusesparfor(MATLAB Coder) to create loops that run in parallel on supported shared-memory multicore platforms in the generated code. If your compiler does not support the Open Multiprocessing (OpenMP) application interface or you disable OpenMP library, MATLAB Coder™ treats theparfor-loops asfor-loops. To find supported compilers, see Supported Compilers. To disable OpenMP library, set theEnableOpenMPproperty of the configuration object tofalse. For details, seecoder.CodeConfig(MATLAB Coder).
rangesearchreturns integer-type (int32) indices in generated standalone C/C++ code. Therefore, the function allows for strict single-precision support when you use single-precision inputs. For MEX code generation, the function still returns double-precision indices to match the MATLAB behavior.
For more information on code generation, see Introduction to Code Generation and General Code Generation Workflow.
Version History
Introduced in R2011b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)