cvloss

Loss for partitioned data at each horizon step

Since R2023b

Syntax

L = cvloss(CVMdl)

L = cvloss(CVMdl,Name=Value)

Description

L = cvloss(CVMdl) returns the loss (mean squared error) obtained by the cross-validated direct forecasting model CVMdl at each step of the horizon (CVMdl.Horizon). For each partition window in CVMdl.Partition and each horizon step, the function computes the loss for the test observations using a model trained on the training observations. CVMdl.X and CVMdl.Y contain all observations.

L = cvloss(CVMdl,Name=Value) specifies additional options using one or more name-value arguments. For example, you can specify a custom loss function.

Examples

Evaluate Model Using Expanding Window Cross-Validation

Create a cross-validated direct forecasting model using expanding window cross-validation. To evaluate the performance of the model:

• Compute the mean squared error (MSE) on each test set using the cvloss object function.

• For each test set, compare the true response values to the predicted response values using the cvpredict object function.

Load the sample file TemperatureData.csv, which contains average daily temperature from January 2015 through July 2016. Read the file into a table. Observe the first eight observations in the table.

Tbl = readtable("TemperatureData.csv");
head(Tbl)

    Year       Month       Day    TemperatureF
    ____    ___________    ___    ____________

    2015    {'January'}     1          23     
    2015    {'January'}     2          31     
    2015    {'January'}     3          25     
    2015    {'January'}     4          39     
    2015    {'January'}     5          29     
    2015    {'January'}     6          12     
    2015    {'January'}     7          10     
    2015    {'January'}     8           4     

Create a datetime variable t that contains the year, month, and day information for each observation in Tbl.

numericMonth = month(datetime(Tbl.Month, ...
    InputFormat="MMMM",Locale="en_US"));
t = datetime(Tbl.Year,numericMonth,Tbl.Day);

Plot the temperature values in Tbl over time.

plot(t,Tbl.TemperatureF)
xlabel("Date")
ylabel("Temperature in Fahrenheit")

Create a direct forecasting model by using the data in Tbl. Train the model using a bagged ensemble of trees. All three of the predictors (Year, Month, and Day) are leading predictors because their future values are known. To create new predictors by shifting the leading predictor and response variables backward in time, specify the leading predictor lags and the response variable lags.

Mdl = directforecaster(Tbl,"TemperatureF", ...
    Learner="bag", ...
    LeadingPredictors="all",LeadingPredictorLags={0:1,0:1,0:7}, ...
    ResponseLags=1:7)

Mdl = 
  DirectForecaster

                  Horizon: 1
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: 2
                 Learners: {[1x1 classreg.learning.regr.CompactRegressionEnsemble]}
                   MaxLag: 7
          NumObservations: 565

Mdl is a DirectForecaster model object. By default, the horizon is one step ahead. That is, Mdl predicts a value that is one step into the future.

Partition the time series data in Tbl using an expanding window cross-validation scheme. Create three training sets and three test sets, where each test set has 100 observations. Note that each observation in Tbl is in at most one test set.

CVPartition = tspartition(size(Mdl.X,1),"ExpandingWindow",3, ...
    TestSize=100)

CVPartition = 
  tspartition

               Type: 'expanding-window'
    NumObservations: 565
        NumTestSets: 3
          TrainSize: [265 365 465]
           TestSize: [100 100 100]
           StepSize: 100

The training sets increase in size from 265 observations in the first window to 465 observations in the third window.

Create a cross-validated direct forecasting model using the partition specified in CVPartition. Inspect the Learners property of the resulting CVMdl object.

CVMdl = crossval(Mdl,CVPartition)

CVMdl = 
  PartitionedDirectForecaster

                Partition: [1x1 tspartition]
                  Horizon: 1
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: 2
                 Learners: {3x1 cell}
                   MaxLag: 7
          NumObservations: 565

CVMdl.Learners

ans=3×1 cell array
    {1x1 timeseries.forecaster.CompactDirectForecaster}
    {1x1 timeseries.forecaster.CompactDirectForecaster}
    {1x1 timeseries.forecaster.CompactDirectForecaster}

CVMdl is a PartitionedDirectForecaster model object. The crossval function trains CVMdl.Learners{1} using the observations in the first training set, CVMdl.Learner{2} using the observations in the second training set, and CVMdl.Learner{3} using the observations in the third training set.

Compute the average test set MSE.

averageMSE = cvloss(CVMdl)

averageMSE = 
53.3480

To obtain more information, compute the MSE for each test set.

individualMSE = cvloss(CVMdl,Mode="individual")

individualMSE = 3×1

   44.1352
   84.0695
   31.8393

The models trained on the first and third training sets seem to perform better than the model trained on the second training set.

For each test set observation, predict the temperature value using the corresponding model in CVMdl.Learners.

predictedY = cvpredict(CVMdl);
predictedY(260:end,:)

ans=306×1 table
    TemperatureF_Step1
    __________________

             NaN      
             NaN      
             NaN      
             NaN      
             NaN      
             NaN      
          50.963      
          57.363      
           57.04      
          60.705      
          59.606      
          58.302      
          58.023      
           61.39      
          67.229      
          61.083      
      ⋮

Only the last 300 observations appear in any test set. For observations that do not appear in a test set, the predicted response value is NaN.

For each test set, plot the true response values and the predicted response values.

tiledlayout(3,1)

nexttile
idx1 = test(CVPartition,1);
plot(t(idx1),Tbl.TemperatureF(idx1))
hold on
plot(t(idx1),predictedY.TemperatureF_Step1(idx1))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Test Set 1")
hold off

nexttile
idx2 = test(CVPartition,2);
plot(t(idx2),Tbl.TemperatureF(idx2))
hold on
plot(t(idx2),predictedY.TemperatureF_Step1(idx2))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Test Set 2")
hold off

nexttile
idx3 = test(CVPartition,3);
plot(t(idx3),Tbl.TemperatureF(idx3))
hold on
plot(t(idx3),predictedY.TemperatureF_Step1(idx3))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Test Set 3")
hold off

Overall, the cross-validated direct forecasting model is able to predict the trend in temperatures. If you are satisfied with the performance of the cross-validated model, you can use the full DirectForecaster model Mdl for forecasting at time steps beyond the available data.

Evaluate Model Using Holdout Validation

Create a partitioned direct forecasting model using holdout validation. To evaluate the performance of the model:

• At each horizon step, compute the root relative squared error (RRSE) on the test set using the cvloss object function.

• At each horizon step, compare the true response values to the predicted response values using the cvpredict object function.

Load the sample file TemperatureData.csv, which contains average daily temperature from January 2015 through July 2016. Read the file into a table. Observe the first eight observations in the table.

Tbl = readtable("TemperatureData.csv");
head(Tbl)

    Year       Month       Day    TemperatureF
    ____    ___________    ___    ____________

    2015    {'January'}     1          23     
    2015    {'January'}     2          31     
    2015    {'January'}     3          25     
    2015    {'January'}     4          39     
    2015    {'January'}     5          29     
    2015    {'January'}     6          12     
    2015    {'January'}     7          10     
    2015    {'January'}     8           4     

Create a datetime variable t that contains the year, month, and day information for each observation in Tbl.

numericMonth = month(datetime(Tbl.Month, ...
    InputFormat="MMMM",Locale="en_US"));
t = datetime(Tbl.Year,numericMonth,Tbl.Day);

Plot the temperature values in Tbl over time.

plot(t,Tbl.TemperatureF)
xlabel("Date")
ylabel("Temperature in Fahrenheit")

Create a direct forecasting model by using the data in Tbl. Specify the horizon steps as one, two, and three steps ahead. Train a model at each horizon using a bagged ensemble of trees. All three of the predictors (Year, Month, and Day) are leading predictors because their future values are known. To create new predictors by shifting the leading predictor and response variables backward in time, specify the leading predictor lags and the response variable lags.

rng("default")
Mdl = directforecaster(Tbl,"TemperatureF", ...
    Horizon=1:3,Learner="bag", ...
    LeadingPredictors="all",LeadingPredictorLags={0:1,0:1,0:7}, ...
    ResponseLags=1:7)

Mdl = 
  DirectForecaster

                  Horizon: [1 2 3]
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: 2
                 Learners: {3x1 cell}
                   MaxLag: 7
          NumObservations: 565

Mdl is a DirectForecaster model object. Mdl consists of three regression models: Mdl.Learners{1}, which predicts one step ahead; Mdl.Learners{2}, which predicts two steps ahead; and Mdl.Learners{3}, which predicts three steps ahead.

Partition the time series data in Tbl using a holdout validation scheme. Reserve 20% of the observations for testing.

holdoutPartition = tspartition(size(Mdl.X,1),"Holdout",0.20)

holdoutPartition = 
  tspartition

               Type: 'holdout'
    NumObservations: 565
        NumTestSets: 1
          TrainSize: 452
           TestSize: 113

The test set consists of the latest 113 observations.

Create a partitioned direct forecasting model using the partition specified in holdoutPartition.

holdoutMdl = crossval(Mdl,holdoutPartition)

holdoutMdl = 
  PartitionedDirectForecaster

                Partition: [1x1 tspartition]
                  Horizon: [1 2 3]
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: 2
                 Learners: {[1x1 timeseries.forecaster.CompactDirectForecaster]}
                   MaxLag: 7
          NumObservations: 565

holdoutMdl is a PartitionedDirectForecaster model object. Because holdoutMdl uses holdout validation rather than a cross-validation scheme, the Learners property of the object contains one CompactDirectForecaster model only.

Like Mdl, holdoutMdl contains three regression models. The crossval function trains holdoutMdl.Learners{1}.Learners{1}, holdoutMdl.Learners{1}.Learners{2}, and holdoutMdl.Learners{1}.Learners{3} using the same training data. However, the three models use different response variables because each model predicts values for a different horizon step.

holdoutMdl.Learners{1}.Learners{1}.ResponseName

ans = 
'TemperatureF_Step1'

holdoutMdl.Learners{1}.Learners{2}.ResponseName

ans = 
'TemperatureF_Step2'

holdoutMdl.Learners{1}.Learners{3}.ResponseName

ans = 
'TemperatureF_Step3'

Compute the root relative squared error (RRSE) on the test data at each horizon step. Use the helper function computeRRSE (shown at the end of this example). The RRSE indicates how well a model performs relative to the simple model, which always predicts the average of the true values. In particular, when the RRSE is less than 1, the model performs better than the simple model.

holdoutRRSE = cvloss(holdoutMdl,LossFun=@computeRRSE)

holdoutRRSE = 1×3

    0.4797    0.5889    0.6103

At each horizon, the direct forecasting model seems to perform better than the simple model.

For each test set observation, predict the temperature value using the corresponding model in holdoutMdl.Learners.

predictedY = cvpredict(holdoutMdl);
predictedY(450:end,:)

ans=116×3 table
    TemperatureF_Step1    TemperatureF_Step2    TemperatureF_Step3
    __________________    __________________    __________________

             NaN                   NaN                   NaN      
             NaN                   NaN                   NaN      
             NaN                   NaN                   NaN      
          41.063                39.758                41.234      
          33.721                36.507                37.719      
          36.987                35.133                37.719      
          38.644                34.598                36.444      
          38.917                34.576                36.275      
          45.888                37.005                 38.34      
          48.516                42.762                 41.05      
          44.882                46.816                43.881      
          35.057                45.301                47.048      
            31.1                41.473                42.948      
          31.817                37.314                42.946      
          33.166                38.419                  41.3      
          40.279                38.432                40.533      
      ⋮

Recall that only the latest 113 observations appear in the test set. For observations that do not appear in the test set, the predicted response value is NaN.

For each test set, plot the true response values and the predicted response values.

tiledlayout(3,1)

idx = test(holdoutPartition);

nexttile
plot(t(idx),Tbl.TemperatureF(idx))
hold on
plot(t(idx),predictedY.TemperatureF_Step1(idx))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Horizon 1")
hold off

nexttile
plot(t(idx),Tbl.TemperatureF(idx))
hold on
plot(t(idx),predictedY.TemperatureF_Step2(idx))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Horizon 2")
hold off

nexttile
plot(t(idx),Tbl.TemperatureF(idx))
hold on
plot(t(idx),predictedY.TemperatureF_Step3(idx))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Horizon 3")
hold off

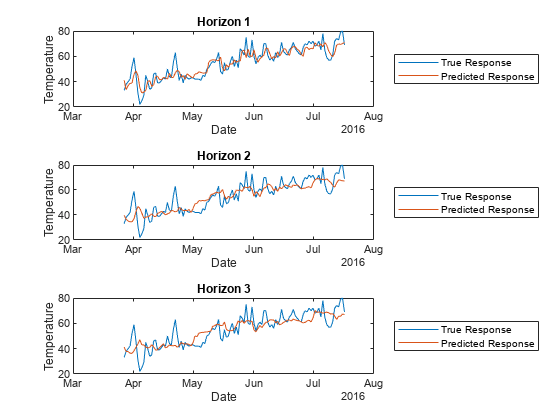
Overall, holdoutMdl is able to predict the trend in temperatures, although it seems to perform best when forecasting one step ahead. If you are satisfied with the performance of the partitioned model, you can use the full DirectForecaster model Mdl for forecasting at time steps beyond the available data.

Helper Function

The helper function computeRRSE computes the RRSE given the true response variable trueY and the predicted values predY. This code creates the computeRRSE helper function.

function rrse = computeRRSE(trueY,predY)
    error = trueY(:) - predY(:);
    meanY = mean(trueY(:),"omitnan");
    rrse = sqrt(sum(error.^2,"omitnan")/sum((trueY(:) - meanY).^2,"omitnan"));
end

Input Arguments

CVMdl — Cross-validated direct forecasting model

PartitionedDirectForecaster model object

Cross-validated direct forecasting model, specified as a PartitionedDirectForecaster model object.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: cvloss(CVMdl,Mode="individual") specifies to return the loss for each window and horizon step combination.

LossFun — Loss function

"mse" (default) | function handle

Loss function, specified as "mse" or a function handle.

• If you specify the built-in function "mse", then the loss function is the mean squared error.

• If you specify your own function using function handle notation, then the function must have the signature lossvalue = lossfun(Y,predictedY), where:

  • The output argument lossvalue is a scalar.

  • You specify the function name (lossfun).

  • Y is an n-by-1 vector of observed numeric responses at a specific horizon step, where n is the number of observations (CVMdl.NumObservations).

  • predictedY is an n-by-1 vector of predicted numeric responses at a specific horizon step.

  Specify your function using LossFun=@lossfun.

Data Types: single | double | function_handle

Mode — Loss aggregation level

"average" (default) | "individual"

Loss aggregation level, specified as "average" or "individual".

Value	Description
"average"	cvloss returns a vector of loss values containing the loss at each horizon step, averaged over all partition windows. At each horizon step, if an observation is in more than one test set, the function averages the predictions for the observation over all test sets before computing the loss.
"individual"	cvloss returns a w-by-h matrix of loss values, where w is the number of partition windows and h is the number of horizon steps (that is, the number of elements in CVMdl.Horizon). Before computing loss values at each horizon step, the function does not average the predictions for observations that are in more than one test set.

Example: Model="individual"

Data Types: char | string

Output Arguments

L — Losses

numeric vector | numeric matrix

Losses, returned as a numeric vector or numeric matrix.

• If Mode is "average", then L is a vector of loss values containing the loss at each horizon step, averaged over all partition windows. At each horizon step, if an observation is in more than one test set, the function averages the predictions for the observation over all test sets before computing the loss.

• If Mode is "individual", then L is a w-by-h matrix of loss values, where w is the number of partition windows and h is the number of horizon steps (that is, the number of elements in CVMdl.Horizon). Before computing the loss values at each horizon step, the function does not average the predictions for observations that are in more than one test set.

Version History

Introduced in R2023b