heaviside
Heaviside step function
Syntax
Description
Examples
The heaviside function returns 0, 1/2, or 1 depending on the argument value. If the argument is a floating-point number (not a symbolic object), then heaviside returns floating-point results.
Evaluate the Heaviside step function for a symbolic input sym(-3). The function heaviside(x) returns 0 for x < 0.
H = heaviside(sym(-3))
H =
Evaluate the Heaviside step function for a symbolic input sym(3). The function heaviside(x) returns 1 for x > 0.
H = heaviside(sym(3))
H =
Evaluate the Heaviside step function for a symbolic input sym(0). The function heaviside(x) returns 1/2 for x = 0.
H = heaviside(sym(0))
H =
For a numeric input x = 0, the function heaviside(x) returns floating-point results.
H = heaviside(0)
H = 0.5000
heaviside takes into account assumptions on variables.
Create a symbolic variable x and assume that it is less than 0.
syms x
assume(x < 0)Evaluate the Heaviside step function for the symbolic input x.
H = heaviside(x)
H =
For further computations, clear the assumptions on x by recreating it using syms.
syms xPlot the Heaviside step function for x and x - 1.
syms x
fplot(heaviside(x), [-2, 2])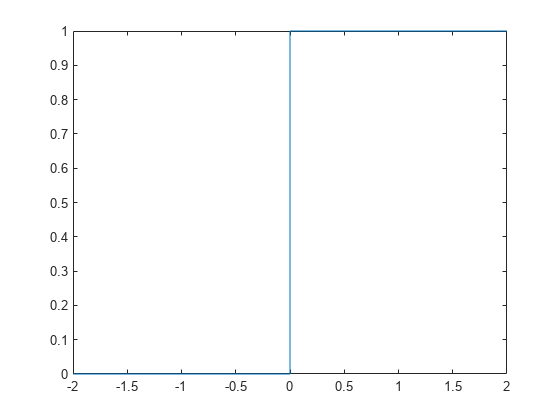
fplot(heaviside(x - 1), [-2, 2])
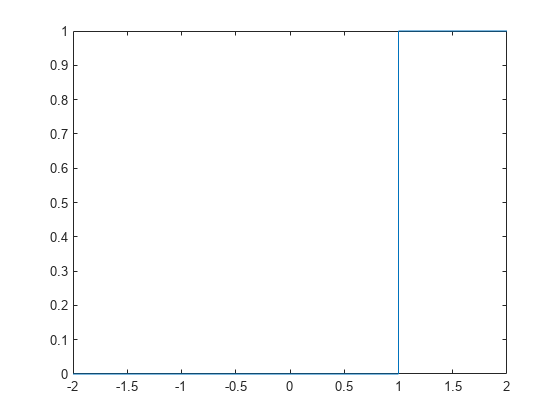
Evaluate the Heaviside function for a symbolic matrix. When the input argument is a matrix, heaviside computes the Heaviside function for each element.
syms x
H = heaviside(sym([-1 0; 1/2 x]))H =
Compute derivatives and integrals of expressions involving the Heaviside function.
Find the first derivative of the Heaviside function. The first derivative of the Heaviside function is the Dirac delta function.
syms x
diff_H = diff(heaviside(x),x)diff_H =
Evaluate the integral .
syms x
int_H = int(exp(-x)*heaviside(x),x,-Inf,Inf)int_H =
The default value of the Heaviside function at the origin is 1/2.
H = heaviside(sym(0))
H =
Other common values for the Heaviside function at the origin are 0 and 1. To change the value of heaviside at the origin, use sympref and specify the value of the "HeavisideAtOrigin" setting. Store the previous parameter value returned by sympref, so that you can restore it later.
oldparam = sympref("HeavisideAtOrigin",1);Check the new value of heaviside at 0.
H = heaviside(sym(0))
H =
The symbolic settings that you set using sympref persist throughout your current and future MATLAB® sessions. To restore the previous value of heaviside at the origin, use the value stored in oldparam.
sympref("HeavisideAtOrigin",oldparam);Alternatively, you can restore the default value of "HeavisideAtOrigin" by using the "default" setting.
sympref("HeavisideAtOrigin","default");
Input Arguments
Input, specified as a number, symbolic number, variable, expression, function, vector, or matrix.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)