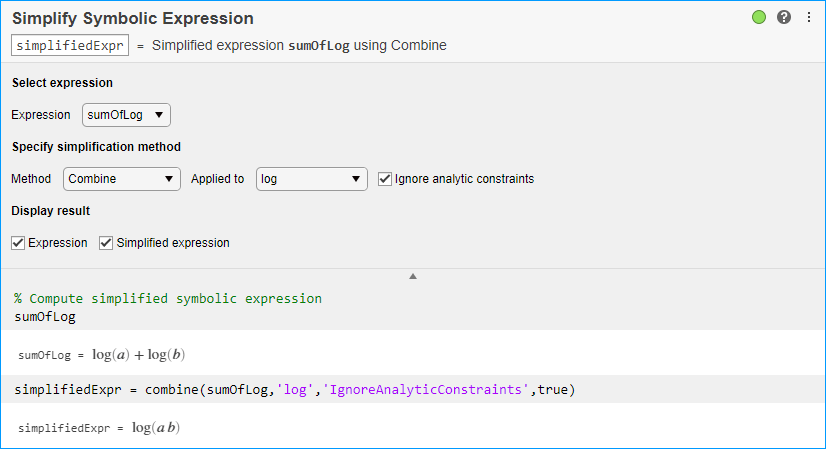
Simplify Symbolic Expression
Simplify symbolic expressions in Live Editor
Open the Task
To add the Simplify Symbolic Expression task to a live script in the MATLAB Editor:
On the Live Editor tab, select Task > Simplify Symbolic Expression.
In a code block in your script, type a relevant keyword, such as
simplify,symbolic,rewrite,expand, orcombine. SelectSimplify Symbolic Expressionfrom the suggested command completions.
Parameters
Algorithms
When you use Ignore analytic constraints, then the simplification
follows some of these rules:
log(a) + log(b) = log(a·b) for all values of a and b. In particular, the following equality is valid for all values of a, b, and c :
(a·b)c = ac·bc.
log(ab) = b·log(a) for all values of a and b. In particular, the following equality is valid for all values of a, b, and c :
(ab)c = ab·c.
If f and g are standard mathematical functions and f(g(x)) = x for all small positive numbers, f(g(x)) = x is assumed to be valid for all complex values of x. In particular:
log(ex) = x
asin(sin(x)) = x, acos(cos(x)) = x, atan(tan(x)) = x
asinh(sinh(x)) = x, acosh(cosh(x)) = x, atanh(tanh(x)) = x
Wk(x·ex) = x for all branch indices k of the Lambert W function.
Version History
Introduced in R2020a