Structure from Motion from Two Views
Structure from motion (SfM) is the process of estimating the 3-D structure of a scene from a set of 2-D images. This example shows you how to estimate the poses of a calibrated camera from two images, reconstruct the 3-D structure of the scene up to an unknown scale factor, and then recover the actual scale factor by detecting an object of a known size.
Overview
This example shows how to reconstruct a 3-D scene from a pair of 2-D images taken with a camera calibrated using the Camera Calibrator app. The algorithm consists of the following steps:
Match a sparse set of points between the two images. There are multiple ways of finding point correspondences between two images. This example detects corners in the first image using the
detectMinEigenFeaturesfunction, and tracks them into the second image usingvision.PointTracker. Alternatively you can useextractFeaturesfollowed bymatchFeatures.Estimate the fundamental matrix using
estimateEssentialMatrix.Compute the motion of the camera using the
estrelposefunction.Match a dense set of points between the two images. Re-detect the point using
detectMinEigenFeatureswith a reduced'MinQuality'to get more points. Then track the dense points into the second image usingvision.PointTracker.Determine the 3-D locations of the matched points using
triangulate.Detect an object of a known size. In this scene there is a globe, whose radius is known to be 10cm. Use
pcfitsphereto find the globe in the point cloud.Recover the actual scale, resulting in a metric reconstruction.
Read a Pair of Images
Load a pair of images into the workspace.
imageDir = fullfile(toolboxdir("vision"),"visiondata","upToScaleReconstructionImages"); images = imageDatastore(imageDir); I1 = readimage(images, 1); I2 = readimage(images, 2); figure imshowpair(I1, I2, 'montage'); title('Original Images');

Load Camera Parameters
This example uses the camera parameters calculated by the Camera Calibrator app. The parameters are stored in the cameraIntrinsics object, and include the camera intrinsics and lens distortion coefficients.
% Load precomputed camera intrinsics data = load("sfmCameraIntrinsics.mat"); intrinsics = data.intrinsics;
Remove Lens Distortion
Lens distortion can affect the accuracy of the final reconstruction. You can remove the distortion from each of the images using the undistortImage function. This process straightens the lines that are bent by the radial distortion of the lens.
I1 = undistortImage(I1, intrinsics); I2 = undistortImage(I2, intrinsics); figure imshowpair(I1, I2, "montage"); title("Undistorted Images");

Find Point Correspondences Between the Images
Detect good features to track. Increase 'MinQuality' to detect fewer points, which would be more uniformly distributed throughout the image. If the motion of the camera is not very large, then tracking using the KLT algorithm is a good way to establish point correspondences.
% Detect feature points imagePoints1 = detectMinEigenFeatures(im2gray(I1), MinQuality=0.1); % Visualize detected points figure imshow(I1, InitialMagnification = 50); title("150 Strongest Corners from the First Image"); hold on plot(selectStrongest(imagePoints1, 150));

% Create the point tracker tracker = vision.PointTracker(MaxBidirectionalError=1, NumPyramidLevels=5); % Initialize the point tracker imagePoints1 = imagePoints1.Location; initialize(tracker, imagePoints1, I1); % Track the points [imagePoints2, validIdx] = step(tracker, I2); matchedPoints1 = imagePoints1(validIdx, :); matchedPoints2 = imagePoints2(validIdx, :); % Visualize correspondences figure showMatchedFeatures(I1, I2, matchedPoints1, matchedPoints2); title("Tracked Features");

Estimate the Essential Matrix
Use the estimateEssentialMatrix function to compute the essential matrix and find the inlier points that meet the epipolar constraint.
% Estimate the fundamental matrix [E, epipolarInliers] = estimateEssentialMatrix(... matchedPoints1, matchedPoints2, intrinsics, Confidence = 99.99); % Find epipolar inliers inlierPoints1 = matchedPoints1(epipolarInliers, :); inlierPoints2 = matchedPoints2(epipolarInliers, :); % Display inlier matches figure showMatchedFeatures(I1, I2, inlierPoints1, inlierPoints2); title("Epipolar Inliers");

Compute the Camera Pose
Compute the location and orientation of the second camera relative to the first one. Note that loc is a translation unit vector, because translation can only be computed up to scale.
relPose = estrelpose(E, intrinsics, inlierPoints1, inlierPoints2);
Reconstruct the 3-D Locations of Matched Points
Re-detect points in the first image using lower 'MinQuality' to get more points. Track the new points into the second image. Estimate the 3-D locations corresponding to the matched points using the triangulate function, which implements the Direct Linear Transformation (DLT) algorithm [1]. Place the origin at the optical center of the camera corresponding to the first image.
% Detect dense feature points. Use an ROI to exclude points close to the % image edges. border = 30; roi = [border, border, size(I1, 2)- 2*border, size(I1, 1)- 2*border]; imagePoints1 = detectMinEigenFeatures(im2gray(I1), ROI = roi, ... MinQuality = 0.001); % Create the point tracker tracker = vision.PointTracker(MaxBidirectionalError=1, NumPyramidLevels=5); % Initialize the point tracker imagePoints1 = imagePoints1.Location; initialize(tracker, imagePoints1, I1); % Track the points [imagePoints2, validIdx] = step(tracker, I2); matchedPoints1 = imagePoints1(validIdx, :); matchedPoints2 = imagePoints2(validIdx, :); % Compute the camera matrices for each position of the camera % The first camera is at the origin looking along the Z-axis. Thus, its % transformation is identity. camMatrix1 = cameraProjection(intrinsics, rigidtform3d); camMatrix2 = cameraProjection(intrinsics, pose2extr(relPose)); % Compute the 3-D points points3D = triangulate(matchedPoints1, matchedPoints2, camMatrix1, camMatrix2); % Get the color of each reconstructed point numPixels = size(I1, 1) * size(I1, 2); allColors = reshape(I1, [numPixels, 3]); colorIdx = sub2ind([size(I1, 1), size(I1, 2)], round(matchedPoints1(:,2)), ... round(matchedPoints1(:, 1))); color = allColors(colorIdx, :); % Create the point cloud ptCloud = pointCloud(points3D, Color=color);
Display the 3-D Point Cloud
Use the plotCamera function to visualize the locations and orientations of the camera, and the pcshow function to visualize the point cloud.
% Visualize the camera locations and orientations cameraSize = 0.3; figure plotCamera(Size=cameraSize, Color="r", Label="1", Opacity=0); hold on grid on plotCamera(AbsolutePose=relPose, Size=cameraSize, ... Color="b", Label="2", Opacity=0); % Visualize the point cloud pcshow(ptCloud, VerticalAxis="y", VerticalAxisDir="down", MarkerSize=45); % Rotate and zoom the plot camorbit(0, -30); camzoom(1.5); % Label the axes xlabel("x-axis"); ylabel("y-axis"); zlabel("z-axis") title("Up to Scale Reconstruction of the Scene");

Fit a Sphere to the Point Cloud to Find the Globe
Find the globe in the point cloud by fitting a sphere to the 3-D points using the pcfitsphere function.
% Detect the globe globe = pcfitsphere(ptCloud, 0.1); % Display the surface of the globe plot(globe); title("Estimated Location and Size of the Globe"); hold off
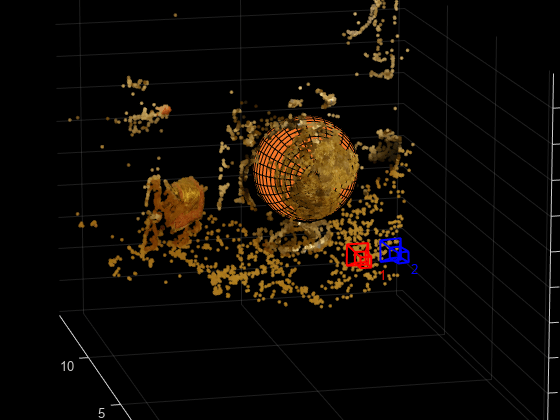
Metric Reconstruction of the Scene
The actual radius of the globe is 10cm. You can now determine the coordinates of the 3-D points in centimeters.
% Determine the scale factor scaleFactor = 10 / globe.Radius; % Scale the point cloud ptCloud = pointCloud(points3D * scaleFactor, Color=color); relPose.Translation = relPose.Translation * scaleFactor; % Visualize the point cloud in centimeters cameraSize = 2; figure plotCamera(Size=cameraSize, Color="r", Label="1", Opacity=0); hold on grid on plotCamera(AbsolutePose=relPose, Size=cameraSize, ... Color="b", Label="2", Opacity=0); % Visualize the point cloud pcshow(ptCloud, VerticalAxis="y", VerticalAxisDir="down", MarkerSize=45); camorbit(0, -30); camzoom(1.5); % Label the axes xlabel("x-axis (cm)"); ylabel("y-axis (cm)"); zlabel("z-axis (cm)") title("Metric Reconstruction of the Scene");

Summary
This example showed you how to recover camera motion and reconstruct the 3-D structure of a scene from two images taken with a calibrated camera.
References
[1] Hartley, Richard, and Andrew Zisserman. Multiple View Geometry in Computer Vision. Second Edition. Cambridge, 2000.