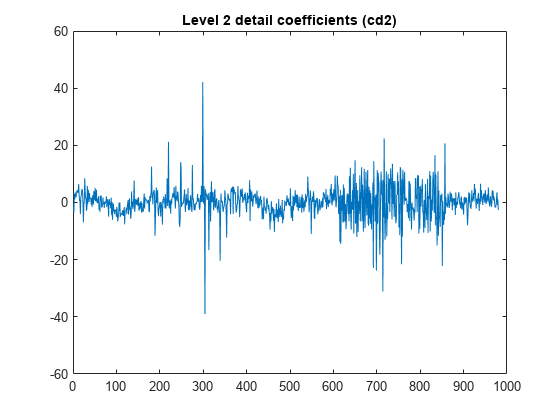
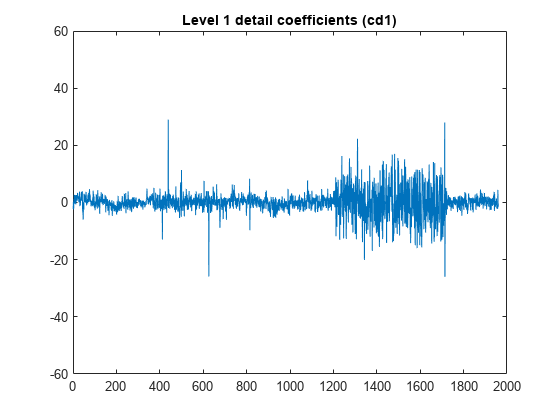
detcoef
1-D detail coefficients
Description
D = detcoef(C,L,N,"cells")D contains the detail coefficients at the
ith specified level.
If
length(N)>1, theD = detcoef(C,L,N)is equivalent toD = detcoef(C,L,N,"cells").D = detcoef(C,L,"cells")is equivalent toD = detcoef(C,L,[1:NMAX]), whereNMAX = length(L)-2.
Examples
Input Arguments
Output Arguments
Extended Capabilities
Version History
Introduced before R2006a