mlptdenoise
Denoise signal using multiscale local 1-D polynomial transform
Syntax
Description
y = mlptdenoise(___,Name,Value)mlpt properties
using one or more Name,Value pair arguments,
and any of the previous syntaxes
[ also returns the thresholded
multiscale local 1–D polynomial transform coefficients.y,T,thresholdedCoefs]
= mlptdenoise(___)
[ also returns the original
multiscale local 1–D polynomial transform coefficients.y,T,thresholdedCoefs,originalCoefs]
= mlptdenoise(___)
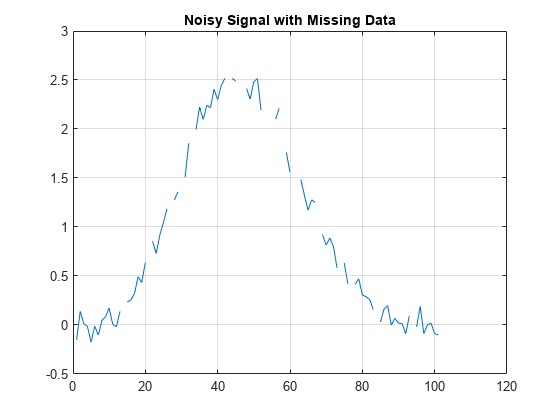
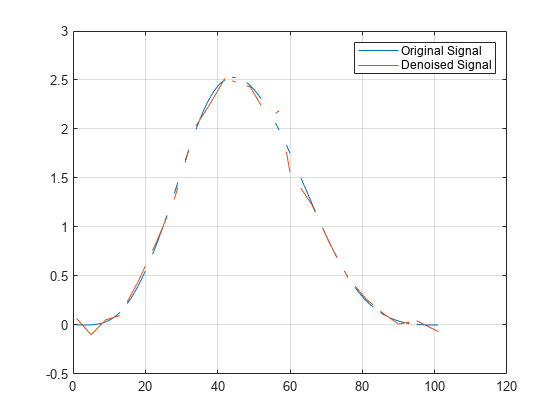
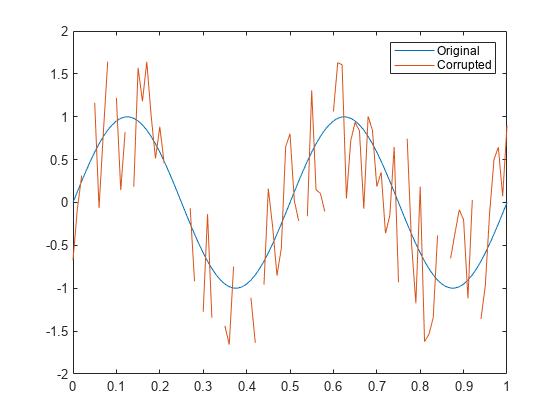
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
Maarten Jansen developed the theoretical foundation of the multiscale
local polynomial transform (MLPT) and algorithms for its efficient
computation [1][2][3]. The MLPT uses a lifting scheme, wherein a kernel
function smooths fine-scale coefficients with a given bandwidth to
obtain the coarser resolution coefficients. The mlpt function uses only local polynomial
interpolation, but the technique developed by Jansen is more general
and admits many other kernel types with adjustable bandwidths [2].
References
[1] Jansen, Maarten. “Multiscale Local Polynomial Smoothing in a Lifted Pyramid for Non-Equispaced Data.” IEEE Transactions on Signal Processing 61, no. 3 (February 2013): 545–55. https://doi.org/10.1109/TSP.2012.2225059.
[2] Jansen, Maarten, and Mohamed Amghar. “Multiscale Local Polynomial Decompositions Using Bandwidths as Scales.” Statistics and Computing 27, no. 5 (September 2017): 1383–99. https://doi.org/10.1007/s11222-016-9692-8.
[3] Jansen, Maarten, and Patrick Oonincx. Second Generation Wavelets and Applications. London ; New York: Springer, 2005.
Version History
Introduced in R2017a