swt2
Discrete stationary 2-D wavelet transform
Description
[
returns the approximation coefficients A,H,V,D] = swt2(X,N,wname)A and the horizontal,
vertical, and diagonal detail coefficients H, V,
and D, respectively, of the stationary 2-D wavelet decomposition of
the image X at level N using the wavelet
wname.
Note
swt2is uses periodic extension.swt2uses double-precision arithmetic internally and returns double-precision coefficient matrices.swt2warns if there is a loss of precision when converting to double.
swc = swt2(___)swc.
Examples
Load and display an image.
load woman imagesc(X) colormap(map) title('Original')

Perform the stationary wavelet decomposition of the image at level 2 using db6.
[ca,chd,cvd,cdd] = swt2(X,2,'db6');Extract the level 1 and level 2 approximation and detail coefficients from the decomposition.
A1 = wcodemat(ca(:,:,1),255); H1 = wcodemat(chd(:,:,1),255); V1 = wcodemat(cvd(:,:,1),255); D1 = wcodemat(cdd(:,:,1),255); A2 = wcodemat(ca(:,:,2),255); H2 = wcodemat(chd(:,:,2),255); V2 = wcodemat(cvd(:,:,2),255); D2 = wcodemat(cdd(:,:,2),255);
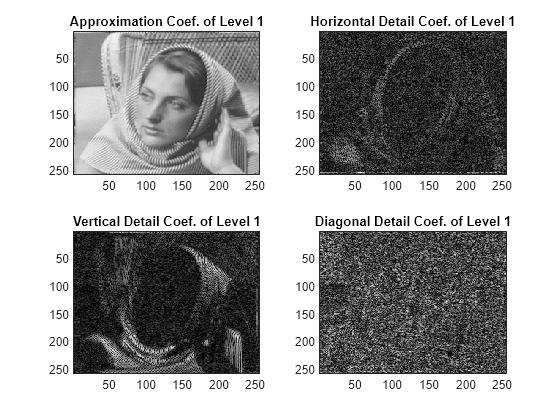
Display the approximation and detail coefficients from the two levels.
subplot(2,2,1) imagesc(A1) title('Approximation Coef. of Level 1') subplot(2,2,2) imagesc(H1) title('Horizontal Detail Coef. of Level 1') subplot(2,2,3) imagesc(V1) title('Vertical Detail Coef. of Level 1') subplot(2,2,4) imagesc(D1) title('Diagonal Detail Coef. of Level 1')
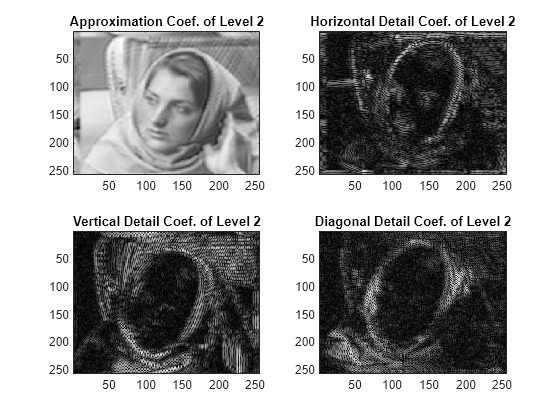
subplot(2,2,1) imagesc(A2) title('Approximation Coef. of Level 2') subplot(2,2,2) imagesc(H2) title('Horizontal Detail Coef. of Level 2') subplot(2,2,3) imagesc(V2) title('Vertical Detail Coef. of Level 2') subplot(2,2,4) imagesc(D2) title('Diagonal Detail Coef. of Level 2')
This example shows how to obtain single-level and multilevel stationary wavelet decompositions of an RGB image.
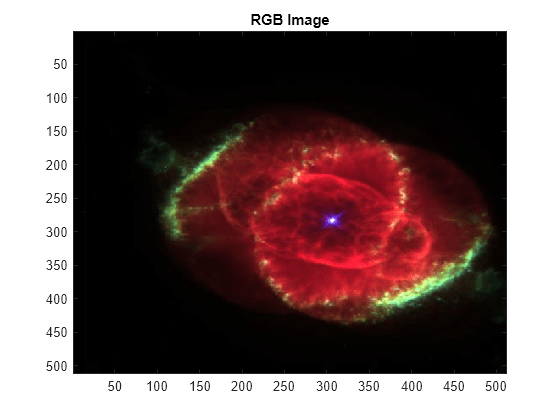
Load and view an RGB image. The image is a 3-D array of type uint8. Since swt2 requires that the first and second dimensions both be divisible by a power of 2, extract a portion of the image.
imdata = imread('ngc6543a.jpg'); x = imdata(1:512,1:512,:); image(x) title('RGB Image')
Obtain the level 4 stationary wavelet decomposition of the image using the db4 wavelet. Return the approximation coefficients. Note the dimensions of the coefficients array.
[a,~,~,~] = swt2(x,4,'db4');
size(a)ans = 1×4
512 512 3 4
The coefficients are all of type double. In an RGB array of type double, each color component is a value between 0 and 1. Rescale the level 2 approximation coefficients to values between 0 and 1 and view the result.
a2 = a(:,:,:,2);
a2 = (a2-min(a2(:)))/(max(a2(:))-min(a2(:)));
image(a2)
title('Level 2 Approximation')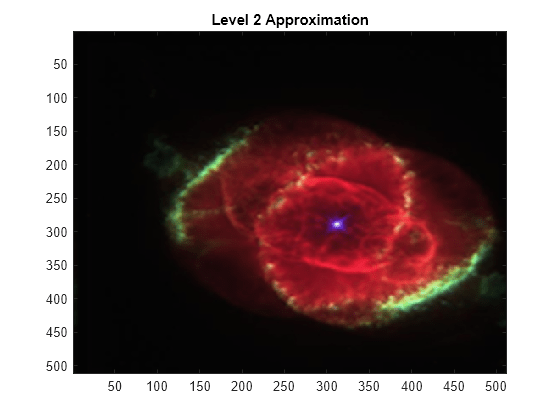
Obtain the single-level stationary wavelet decomposition of the image using the db4 wavelet. Return the approximation coefficients. In a single-level decomposition of an RGB image, the third dimension is singleton.
[a,~,~,~] = swt2(x,1,'db4');
size(a)ans = 1×4
512 512 1 3
View the approximation coefficients. To prevent an error when using image, squeeze the approximation coefficients array to remove the singleton dimension.
a2 = squeeze(a);
a2 = (a2-min(a(:)))/(max(a(:))-min(a(:)));
image(a2)
title('Approximation')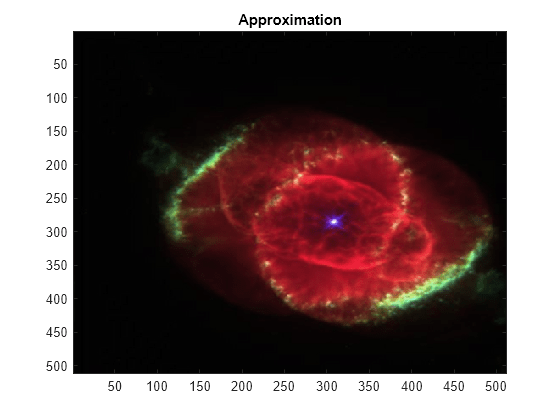
Input Arguments
Input image, specified as a real-valued 2-D matrix or real-valued 3-D array. If
X is 3-D, X is assumed to be an RGB image,
also referred to as a truecolor image, and the third dimension of
X must equal 3. For more information on truecolor images, see
Working with Image Types in MATLAB.
Data Types: double
Level of decomposition, specified as a positive integer.
2N must divide size(X,1) and
size(X,2). Use wmaxlev to determine the maximum level of decomposition.
Analyzing wavelet, specified as a character vector or string scalar.
swt2 supports only Type 1 (orthogonal) or Type 2 (biorthogonal)
wavelets. See wfilters for a list of orthogonal and
biorthogonal wavelets.
Wavelet decomposition filters, specified as a pair of even-length real-valued
vectors. LoD is the lowpass decomposition filter, and
HiD is the highpass decomposition filter. The lengths of
LoD and HiD must be equal. See wfilters for additional information.
Output Arguments
Approximation coefficients, returned as a multidimensional array. The dimensions of
A depend on the dimensions of the input X
and the level of decomposition N.
If
Xis m-by-n:If
Nis greater than 1, thenAis m-by-n-by-N. For 1 ≤ i ≤N,A(:,:,i)contains the approximation coefficients at level i.If
Nis equal to 1, thenAis m-by-n.
If
Xis m-by-n-by-3:If
Nis greater than 1, thenAis m-by-n-by-3-by-N. For 1 ≤ i ≤Nandj = 1, 2, 3,A(:,:,j,i)contains approximation coefficients at level i.If
Nis equal to 1, thenAis m-by-n-by-1-by-3. Since MATLAB® removes singleton last dimensions by default, the third dimension is singleton.
Data Types: double
Detail coefficients, returned as multidimensional arrays of equal size.
H, V, and D contain the
horizontal, vertical, and diagonal detail coefficients, respectively. The dimensions of
the arrays depend on the dimensions of the input X and the level of
decomposition N.
If
Xis m-by-n:If
Nis greater than 1, the arrays are m-by-n-by-N. For 1 ≤ i ≤N,H(:,:,i),V(:,:,i), andD(:,:,i)contain the detail coefficients at level i.If
Nis equal to 1, the arrays are m-by-n.
If
Xis m-by-n-by-3:If
Nis greater than 1, the arrays are m-by-n-by-3-by-N. For 1 ≤ i ≤Nandj = 1, 2, 3,H(:,:,j,i),V(:,:,j,i), andD(:,:,j,i)contain the detail coefficients at level i.If
Nis equal to 1, the arrays are m-by-n-by-1-by-3. Forj = 1, 2, 3,H(:,:,1,j),V(:,:,1,j)andD(:,:,1,j)contain the detail coefficients. Since MATLAB removes singleton last dimensions by default, the third dimension is singleton.
Data Types: double
Stationary wavelet decomposition, returned as a multidimensional array.
swc is the concatenation of the approximation coefficients
A and detail coefficients H,
V, and D.
Algorithms
For images, a stationary wavelet transform (SWT) algorithm similar to the one-dimensional case is possible for two-dimensional wavelets and scaling functions obtained from one-dimensional functions by tensor product. This kind of two-dimensional SWT leads to a decomposition of approximation coefficients at level j into four components: the approximation at level j+1, and the details in three orientations (horizontal, vertical, and diagonal).
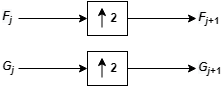
This chart describes the basic decomposition step for images.

where
 — Convolve the rows of the entry with filter
X.
— Convolve the rows of the entry with filter
X. — Convolve the columns of the entry with filter
X.
— Convolve the columns of the entry with filter
X.
Initialization
cA0 = s
F0 =
LoDG0 =
HiD-
where
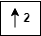 denotes upsample.
denotes upsample.
Note that size(cAj) =
size(cDj(h)) =
size(cDj(v)) =
size(cDj(d)) =
s, where s equals the size of the
analyzed image.
To distinguish a single-level decomposition of a truecolor image from a multilevel decomposition of an indexed image, the approximation and detail coefficient arrays of truecolor images are 4-D arrays.
If you perform a multilevel decomposition, the dimensions of
A,H,V, andDare m-by-n-by-3-by-k, where k is the level of decomposition.If you perform a single-level decomposition, the dimensions of
A,H,V, andDare m-by-n-by-1-by-3. Since MATLAB removes singleton last dimensions by default, the third dimension of the arrays is singleton.
References
[1] Nason, G. P., and B. W. Silverman. “The Stationary Wavelet Transform and Some Statistical Applications.” In Wavelets and Statistics, edited by Anestis Antoniadis and Georges Oppenheim, 103:281–99. New York, NY: Springer New York, 1995. https://doi.org/10.1007/978-1-4612-2544-7_17.
[2] Coifman, R. R., and D. L. Donoho. “Translation-Invariant De-Noising.” In Wavelets and Statistics, edited by Anestis Antoniadis and Georges Oppenheim, 103:125–50. New York, NY: Springer New York, 1995. https://doi.org/10.1007/978-1-4612-2544-7_9.
[3] Pesquet, J.-C., H. Krim, and H. Carfantan. “Time-Invariant Orthonormal Wavelet Representations.” IEEE Transactions on Signal Processing 44, no. 8 (August 1996): 1964–70. https://doi.org/10.1109/78.533717.
Extended Capabilities
Usage notes and limitations:
The input wavelet name must be constant.
The input level of decomposition must be defined as a scalar during compilation.
Version History
Introduced before R2006aTo distinguish a single-level decomposition of a truecolor image from a multilevel decomposition of an indexed image, the approximation and detail coefficient arrays of truecolor images are 4-D arrays.
Migrate from Previous Releases to R2017b
Depending on the original input data type and level of wavelet decomposition, you might have to take different steps to make
swt2coefficient arrays from previous releases compatible with R2017b coefficient arrays. The steps depend on whether you have a single coefficient array or separate approximation and detail coefficient arrays.Single Coefficient Array Multiple Coefficient Arrays Input: Index image
Single-level: No compatibility issues
Multi-level: No compatibility issues
Input: Index image
Single-level: No compatibility issues
Multi-level: No compatibility issues
Input: Truecolor image
Single-level: If
swcis the output ofswt2from a previous release, execute:swc1 = double(swc);
Multi-level: If
swcis the output ofswt2from a previous release, execute:swc1 = double(swc);
Input: Truecolor image
Single-level: If
ca,chd,cvd, andcddare outputs ofswt2from a previous release, execute:ca1 = double(ca); chd1 = double(chd); cvd1 = double(cvd); cdd1 = double(cdd); ca2 = reshape(ca1,[m,n,1,3]); chd2 = reshape(chd1,[m,n,1,3]); cvd2 = reshape(cvd1,[m,n,1,3]); cdd2 = reshape(cdd1,[m,n,1,3]);
Multi-level: If
ca,chd,cvd, andcddare outputs ofswt2from a previous release, execute:ca1 = double(ca); chd1 = double(chd); cvd1 = double(cvd); cdd1 = double(cdd);
Migrate from R2017b to Previous Releases
Depending on the original input data type and level of wavelet decomposition, you might have to take different steps to make R2017b
swt2coefficient arrays compatible with the coefficient arrays from previous releases. The steps depend on whether you have a single coefficient array or separate approximation and detail coefficient arrays.Single Coefficient Array Multiple Coefficient Arrays Input: Index image
Single-level: No compatibility issues
Multi-level: No compatibility issues
Input: Index image
Single-level: No compatibility issues
Multi-level: No compatibility issues
Input: Truecolor image
Single-level: No compatibility issues
Multi-level: No compatibility issues
Input: Truecolor image
Single-level: If
ca,chd,cvd, andcddare outputs ofswt2from R2017b, execute:ca1 = single(squeeze(ca)); chd1 = single(squeeze(chd)); cvd1 = single(squeeze(cvd)); cdd1 = single(squeeze(cdd));
Multi-level: No compatibility issues
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)