wmulden
Wavelet multivariate denoising
Syntax
Description
[
returns a denoised version x_den,npc,nestcov,dec_den,pca_params,den_params]
= wmulden(x,level,wname,npc_app,npc_fin,tptr,sorh)x_den of the input matrix
x. The strategy combines univariate wavelet denoising in
the basis where the estimated noise covariance matrix is diagonal with noncentered
Principal Component Analysis (PCA) on approximations in the wavelet domain or with
final PCA.
[dec,
returns the wavelet decomposition pca_params]
= wmulden("estimate",dec,npc_app,npc_fin)dec and the principal
components estimates pca_params.
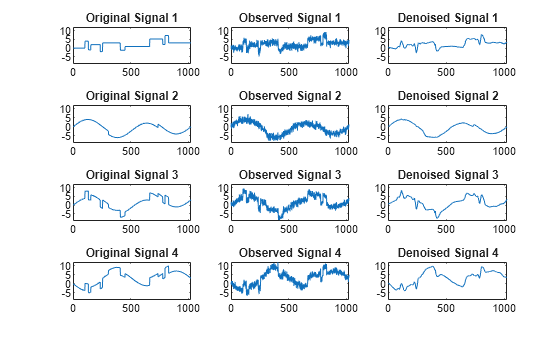
Examples
Input Arguments
Output Arguments
Algorithms
The multivariate denoising procedure is a generalization of the one-dimensional strategy. It combines univariate wavelet denoising in the basis where the estimated noise covariance matrix is diagonal and non-centered Principal Component Analysis (PCA) on approximations in the wavelet domain or with final PCA.
The robust estimate of the noise covariance matrix given by the minimum covariance determinant estimator based on the matrix of finest details.
References
[1] Aminghafari, Mina, Nathalie Cheze, and Jean-Michel Poggi. “Multivariate Denoising Using Wavelets and Principal Component Analysis.” Computational Statistics & Data Analysis 50, no. 9 (May 2006): 2381–98. https://doi.org/10.1016/j.csda.2004.12.010.
[2] Rousseeuw, Peter J., and Katrien Van Driessen. “A Fast Algorithm for the Minimum Covariance Determinant Estimator.” Technometrics 41, no. 3 (August 1999): 212–23. https://doi.org/10.1080/00401706.1999.10485670.
Version History
Introduced in R2006b