Signal Processing Toolbox provides functions and apps to manage, analyze, preprocess, and extract features from uniformly and nonuniformly sampled signals. The toolbox includes tools for filter design and analysis, resampling, smoothing, detrending, and power spectrum estimation. You can use the Signal Analyzer app for visualizing and processing signals simultaneously in time, frequency, and time-frequency domains. With the Filter Designer app you can design and analyze FIR and IIR digital filters. Both apps generate MATLAB scripts to reproduce or automate your work.
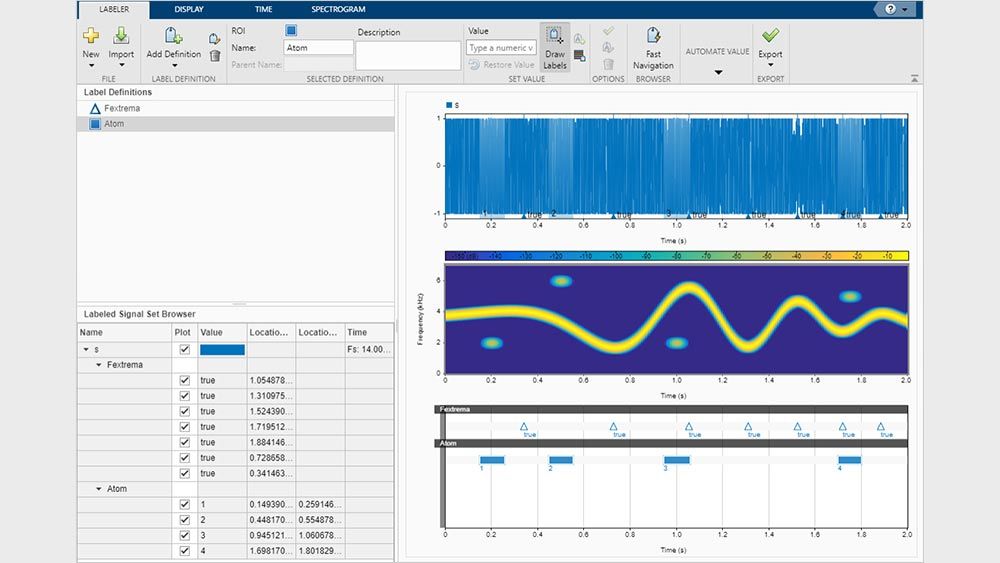
Using toolbox functions, you can prepare signal datasets for AI model training by engineering features that reduce dimensionality and improve the quality of signals. You can access and process collections of files and large datasets using signal datastores. With the Signal Labeler app, you can annotate signal attributes, regions, and points of interest to create labeled signal sets. The toolbox supports GPU acceleration in addition to C/C++ and CUDA® code generation for desktop prototyping and embedded system deployment.
Machine Learning and Deep Learning for Signals
Perform preprocessing, feature engineering, signal labeling, and dataset generation for machine learning and deep learning workflows. Use the Signal Labeler app to create ground truth datasets and extract features to train AI models.
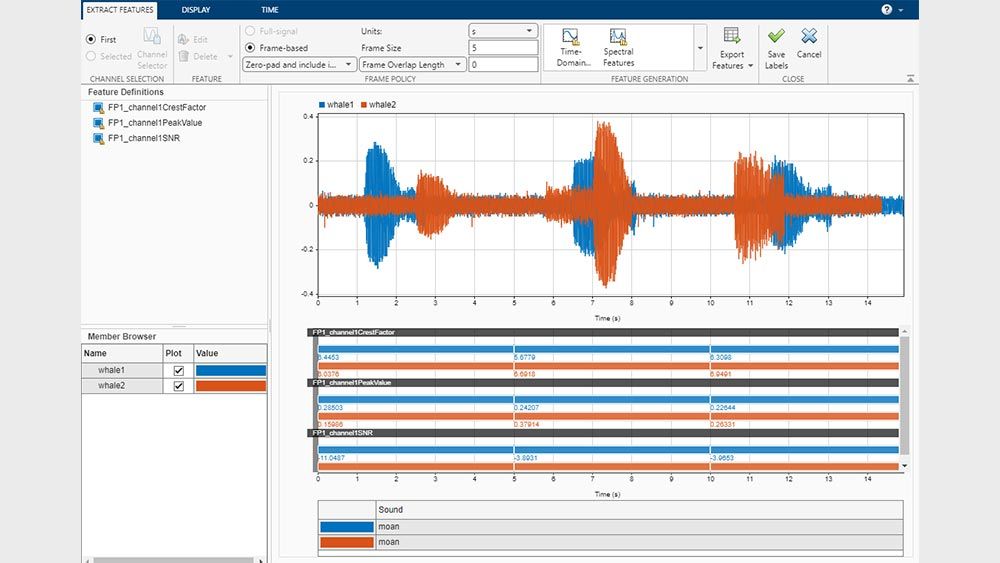
Feature Extraction and Signal Measurements
Measure and extract distinctive features in signals including peaks, power, bandwidth, distortion, and signal statistics. Compute metrics related to pulses and transitions. Extract features for an entire dataset using the Signal Labeler app.
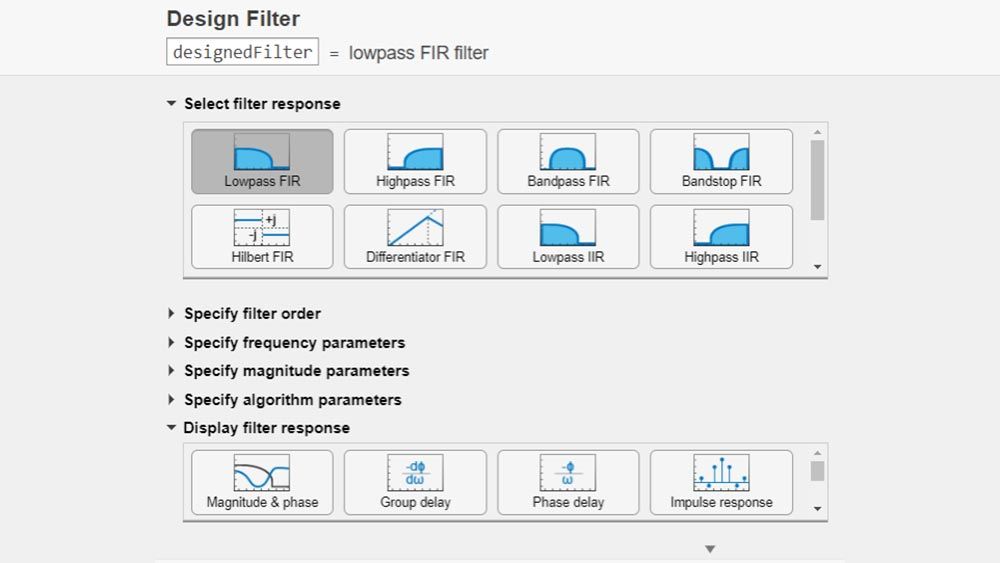
Filter Design and Analysis
Design, analyze, and implement digital and analog filters. Use the Filter Designer app or the Design Filter live editor task to design a variety of digital FIR and IIR filters, such as lowpass, highpass, and bandstop.
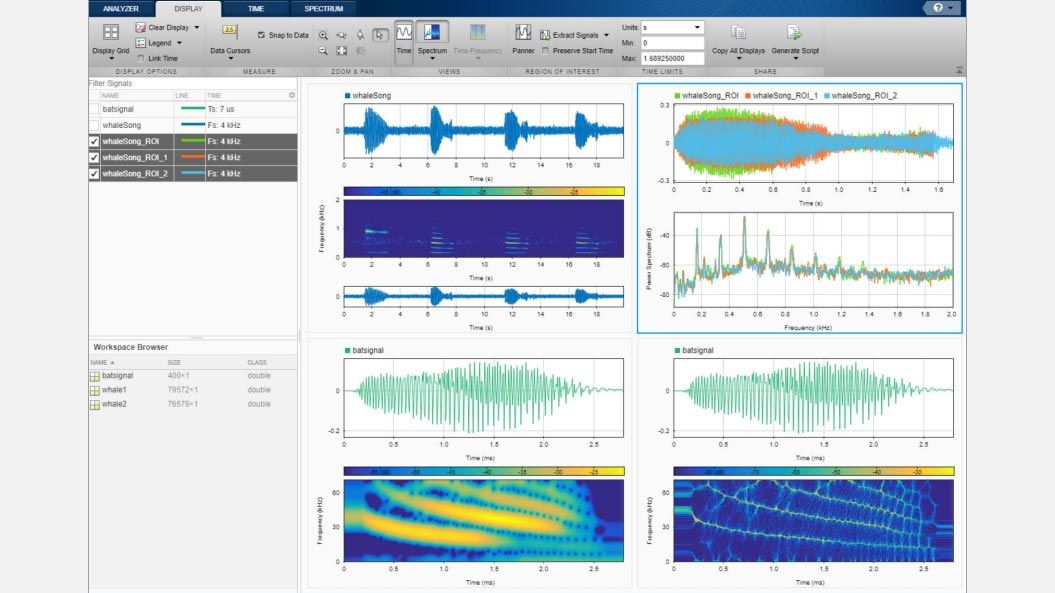
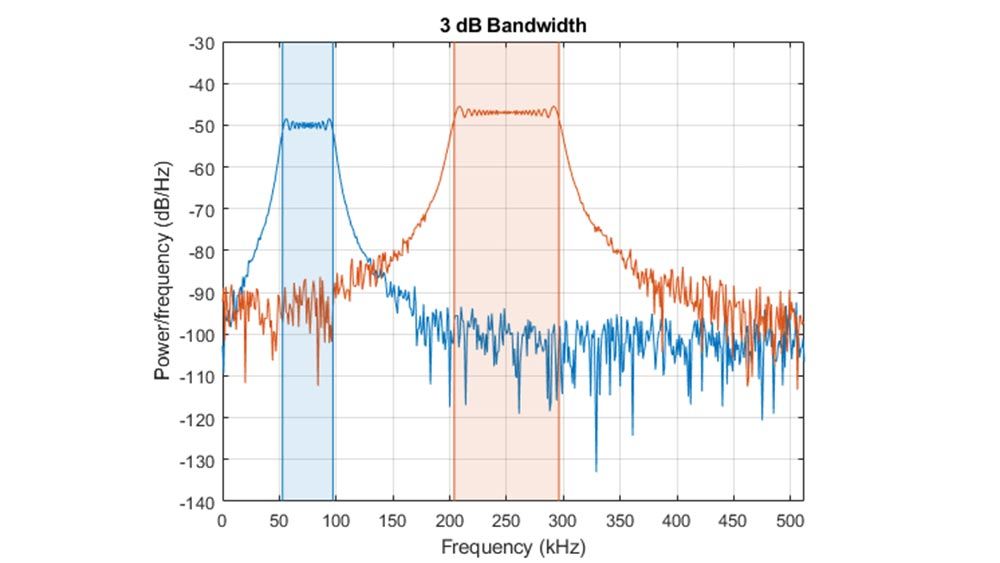
Spectral Analysis
Characterize the frequency content of a signal using spectral estimation and subspace techniques. Design, visualize, and implement windowing functions.
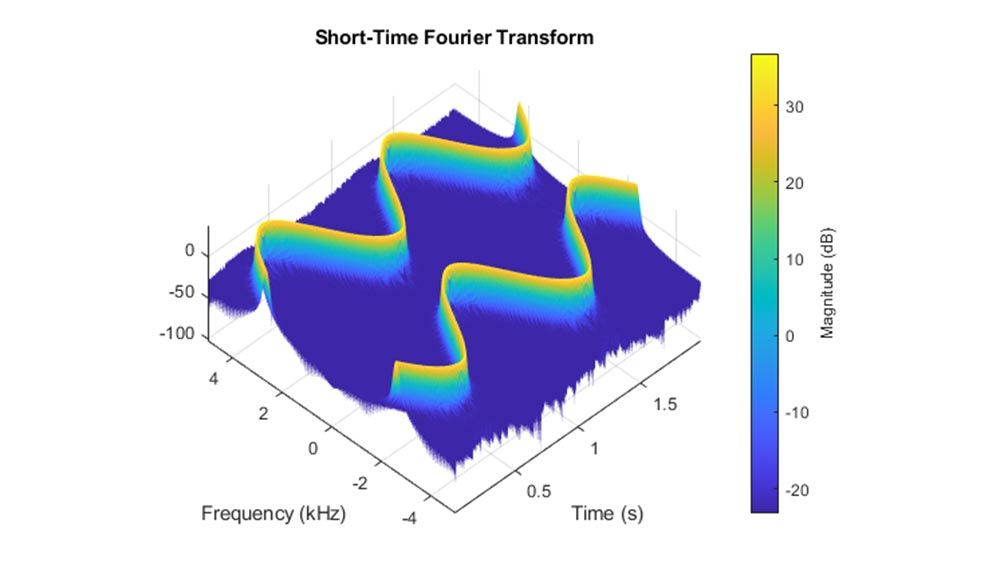
Time-Frequency Analysis
Visualize and compare time-frequency content of nonstationary signals using methods such as spectrogram, synchrosqueezing, and reassignment.
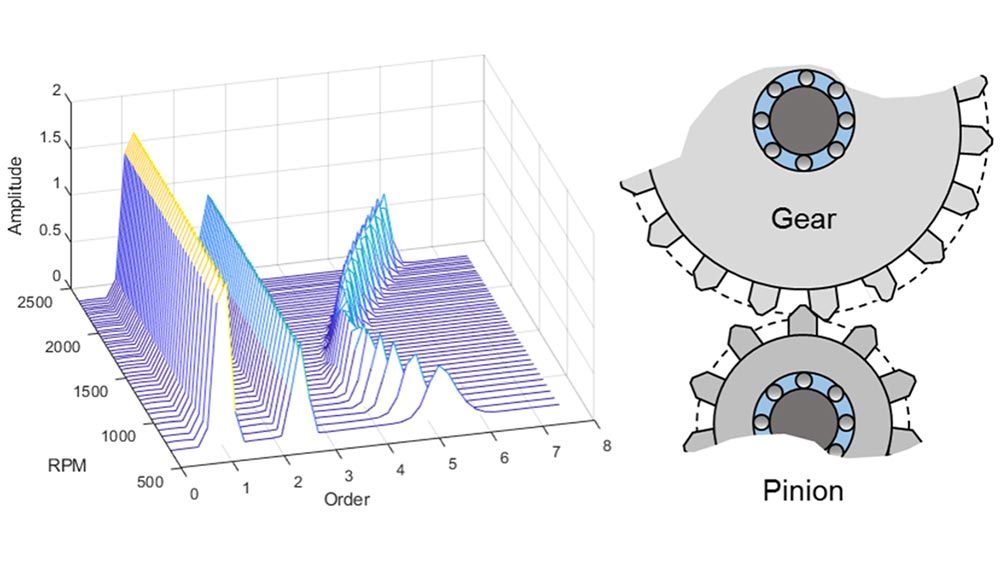
Vibration Analysis
Characterize vibrations in mechanical systems. Use order analysis to analyze and visualize spectral content occurring in rotating machinery. Perform experimental modal analysis and fatigue analysis.
Code Acceleration and Generation
Accelerate the execution of your signal processing algorithms using a Graphics Processing Unit (GPU). Generate portable C/C++ source code, standalone executables, or standalone applications from your MATLAB code.
Product Resources:
Get a Free Trial
30 days of exploration at your fingertips.
Ready to Buy?
Get pricing information and explore related products.
Are You a Student?
Your school may already provide access to MATLAB, Simulink, and add-on products through a campus-wide license.