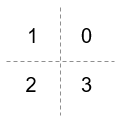comm.QPSKDemodulator
(To be removed) Demodulate using QPSK method
comm.QPSKDemodulator will be removed in a future release. Use pskdemod instead. For information on updating your code, see Version History.
Description
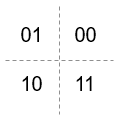
The comm.QPSKDemodulator object demodulates a signal that was modulated using the
quadrature phase shift keying (QPSK) method. The input is a baseband representation of the
modulated signal.
To demodulate a signal that was modulated using the QPSK method:
Create the
comm.QPSKDemodulatorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
qpskdemod = comm.QPSKDemodulator creates a System object™ to demodulate input QPSK signals.
qpskdemod = comm.QPSKDemodulator(
sets properties using one or more name-value arguments. For example,
Name=Value)DecisionMethod="Hard decision" specifies demodulation using the
hard-decision method.
qpskdemod = comm.QPSKDemodulator(
sets the phase=Name,Value)PhaseOffset property to
phase, and optional name-value arguments. Specify
phase in radians.
Properties
Usage
Description
y = qpskdemod(x,var)var. This syntax
applies when you set the BitOutput property to
true, the DecisionMethod property to
'Approximate log-likelihood ratio' or 'Log-likelihood
ratio', and the VarianceSource property to
'Input port'.
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)