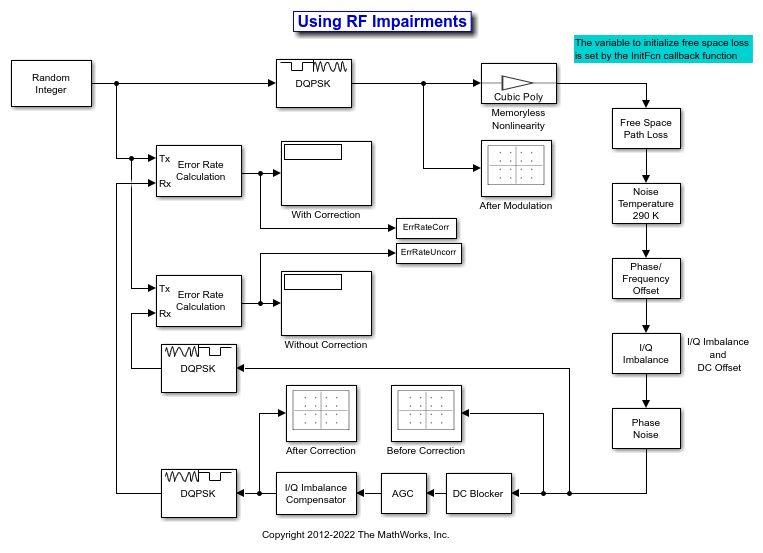
Receiver Thermal Noise
Apply receiver thermal noise to complex signal
Libraries:
Communications Toolbox /
RF Impairments and Components
Description
The Receiver Thermal Noise block applies receiver thermal noise to a complex signal. The block simulates the effects of thermal noise on a complex signal. The Specification method parameter enables specification of the thermal noise based on the noise temperature, noise figure, or noise factor.
Examples
Extended Examples
Limitations
To use this block in a For Each Subsystem (Simulink) you must set
Random number sourcetoGlobal Streamand the model toNormalorAcceleratorsimulation mode. This ensures that each run will generate independent noise samples.
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Algorithms
Wireless receiver performance is often expressed as a noise factor or figure. The noise factor, F, is defined as the ratio of the input signal-to-noise ratio, Si/Ni to the output signal-to-noise ratio, So/No, such that
Given the receiver gain G and receiver noise power Nckt, the noise factor can be expressed as
The IEEE® defines the noise factor assuming that noise temperature at the input is T0, where T0 = 290 K. The noise factor is then
k is Boltzmann's constant. B is the signal bandwidth. Tckt is the equivalent input noise temperature of the receiver and is expressed as
The overall noise temperature of an antenna and receiver Tsys is
where Tant is the antenna noise temperature.
The noise figure NF is the dB equivalent of the noise factor and can be expressed as
The noise power can be expressed as
where V is the noise voltage expressed as
and R is the reference load.
Extended Capabilities
Version History
Introduced before R2006aSee Also
Blocks
- I/Q Imbalance | Free Space Path Loss | Memoryless Nonlinearity | Phase Noise | Phase/Frequency Offset