TPC Encoder
Turbo product code (TPC) encoder
Libraries:
Communications Toolbox /
Error Detection and Correction /
Block
Description
The TPC Encoder block performs 2-D turbo product code (TPC) encoding of an input message. The product code is a 2-D concatenation of linear block codes. The linear block codes can be a parity check code, a Hamming code, or a BCH code capable of correcting two errors. Extended and shortened codes can be applied independently on each dimension. For a description of 2-D TPC encoding, see Turbo Product Code Construction.
For information about valid code pairs and the error-correcting capability for each valid code pair, see Component Code Pairs.
Examples
Perform error rate calculations for a transmission signal that has been TPC encoded and decoded.
A random signal is TPC encoded, QPSK modulated, filtered through an AWGN channel, and QPSK demodulated. The bipolar mapping is converted from negative to positive mapping and then the signal is TPC decoded. An error rate calculation compares the original message to the recovered message.
Open Example Model and Explore Its Contents
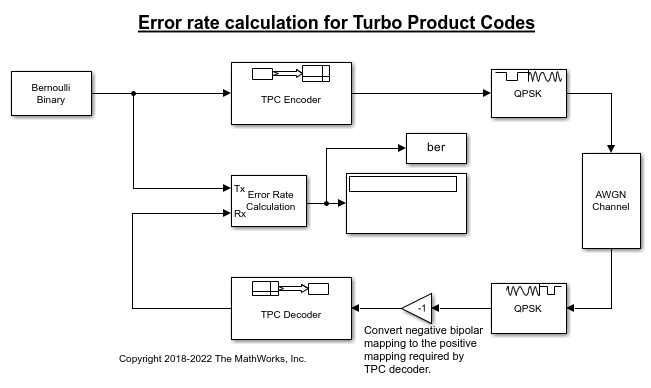
Several settings must be aligned with each other to synchronize encoding and decoding of the message. Start by deciding on a code rate, and aligning the TPC Encoder and TPC Decoder 2-D [N,K] pairs. For this example the default settings are used, [Nr,Kr] = [15,11] and [Nc,Kc] = [32,26].
The number of samples per frame and the sample time used by the Bernoulli Binary Generator block are determined based on the message length parameters, Number of rows in message, Kr and Number of columns in message, Kc.
Number of samples per frame = (Kr*Kc) = 286
Sample time = 1/(Kr*Kc) = 0.0035.
The white Gaussian noise the SNR setting is calculated based on the coding rate, modulation order, and Eb/N0.
Modulation order, M = 2
Eb/N0 = -11
rate = (Kr*Kc)/((Nr-Kr)*(Nc-Kc)) = 14.3
snr = 10*log10(M*rate*10^(ebn0/10)) = 3.5637
The noise variance used in the QPSK Demodulator Baseband block is calculated based on the SNR.
Noise variance = 1/10^(snr/10) = 1/10^(3.5637/10) = 0.4402
Run the model and observe the error rate calculation. Results will vary from run to run due to the use of random input data.
Bit error rate: 0.00042
Further Exploration
To run the model yourself, open the example using the button provided or by entering open slex_tpc_err_rate_calc at the MATLAB® command prompt. Consider modifying the model to change the signal to noise ratio. When adjusting TPC Encoder settings be sure to align settings in the TPC Decoder, Bernoulli Binary Generator, AWGN Channel, and QPSK Demodulator Baseband.
Ports
Input
Input message bits to encode, specified as a column vector.
For full-length input messages, the length of the column vector must be the product of Number of rows in message, Kr and Number of columns in message, Kc.
For shortened input messages, the length of the column vector must be the product of Number of rows in shortened message, Sr and Number of columns in shortened message, Sc.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean
Output
TPC-encoded message, returned as a column vector with the same data type as the input signal.
For full-length input messages, the length of the column vector is the product of Number of rows in code, Nr and Number of columns in code, Nc.
For shortened input messages, the length of the column vector is the product of (NR–KR+SR) and (NC–KC+SC), where:
NR is the value of Number of rows in code, Nr.
KR is the value of Number of rows in message, Kr.
SR is the value of Number of rows in shortened message, Sr.
NC is the value of Number of columns in code, Nc.
KC is the value of Number of columns in message, Kc.
SC is the value of Number of columns in shortened message, Sc.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Row TPC parameters
When Extended codes is selected, the lists for Number of rows in code, Nr and Number of rows in message, Kr contain the valid values for extended individual code pairs (NR,KR).
When Extended codes is cleared, the lists for Number of rows in code, Nr and Number of rows in message, Kr contain the valid values for nonextended individual code pairs (NR,KR).
Number of rows in the product code matrix, NR. The list of integer values varies depending on the setting for Extended codes.
Number of rows in the message matrix, KR. The list of integer values varies depending on the setting for Extended codes and Number of rows in code, Nr.
Select Specify shortened message length to specify a value for Number of rows in shortened message, Sr.
Number of rows in the shortened message matrix, SR, specified as an integer less than or equal to KR. When you specify this parameter, provide full-length NR and KR values to specify the (NR,KR) code pair. This code pair is then shortened to the (NR–KR+SR,SR) code pair, where:
NR is the value of Number of rows in code, Nr.
KR is the value of Number of rows in message, Kr.
SR is the value of Number of rows in shortened message, Sr.
Dependencies
To enable this parameter, select Specify shortened message length.
Column TPC parameters
When Extended codes is selected, the lists for Number of columns in code, Nc and Number of columns in message, Kc contain the valid values for extended individual code pairs (NC,KC).
When Extended codes is cleared, the lists for Number of columns in code, Nc and Number of columns in message, Kc contain the valid values for nonextended individual code pairs (NC,KC).
Number of columns in the product code matrix, NC. The list of integer values varies depending on the setting for Extended codes.
Number of columns in the message matrix, KC. The list of integer values varies depending on the setting for Extended codes and Number of columns in code, Nc.
Select Specify shortened message length to specify a value for Number of columns in shortened message, Sc.
Number of columns in the shortened message matrix, SC, specified as an integer. When you specify this parameter, provide full-length NC and KC values to specify the (NC,KC) code pair. This code pair is then shortened to the (NC–KC+SC, SC) code pair, where:
NC is the value of Number of columns in code, Nc.
KC is the value of Number of columns in message, Kc.
SC is the value of Number of columns in shortened message, Sc.
Dependencies
To enable this parameter, select Specify shortened message length.
Type of simulation to run, specified as Code generation or
Interpreted execution.
Code generation— Simulate the model by using generated C code. The first time you run a simulation, Simulink generates C code for the block. The model reuses the C code for subsequent simulations unless the model changes. This option requires additional startup time, but the speed of the subsequent simulations is faster than with theInterpreted executionoption.Interpreted execution— Simulate the model by using the MATLAB® interpreter. This option shortens startup time, but the speed of subsequent simulations is slower than with theCode generationoption. In this mode, you can debug the source code of the block.
For more information, see Interpreted Execution vs. Code Generation (Simulink).
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
More About
This table lists the supported component code pairs for the row (NR,KR) and column (NC,KC) parameters.
NR and KR represent the number of rows in the product code matrix and message matrix, respectively.
NC and KC represent the number of columns in the product code matrix and message matrix, respectively.
Within each code type, any two component code pairs can form a 2-D TPC code. The table also includes the error-correction capability for each code pair.
| Code type | Component Code Pairs(NR,KR) and (NC,KC) | Error-Correction Capability (T) |
| Hamming code | (255,247) | 1 |
| (127,120) | 1 | |
| (63,57) | 1 | |
| (31,26) | 1 | |
| (15,11) | 1 | |
| (7,4) | 1 | |
| Extended Hamming code | (256,247) | 1 |
| (128,120) | 1 | |
| (64,57) | 1 | |
| (32,26) | 1 | |
| (16,11) | 1 | |
| (8,4) | 1 | |
| BCH code | (255,239) | 2 |
| (127,113) | 2 | |
| (63,51) | 2 | |
| (31,21) | 2 | |
| (15,7) | 2 | |
| Extended BCH code | (256,239) | 2 |
| (128,113) | 2 | |
| (64,51) | 2 | |
| (32,21) | 2 | |
| (16,7) | 2 | |
| Parity check code | (256,255) | - |
| (128,127) | - | |
| (64,63) | - | |
| (32,31) | - | |
| (16,15) | - | |
| (8,7) | - | |
| (4,3) | - |
Turbo product codes (TPC) are a form of concatenated codes used as forward error-correcting (FEC) codes. Two or more component block codes, such as systematic linear block codes, are used to construct TPCs. This encoder implements 2-D product code encoding, as described in [1], using two Linear Block Codes.
The TPC encoder accepts either full-length or shortened messages.
 Construction of Full-Length Message Product Codes
Construction of Full-Length Message Product Codes
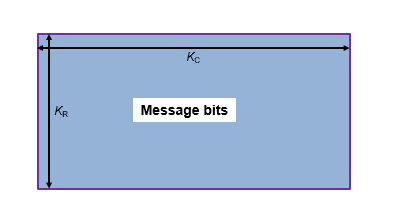
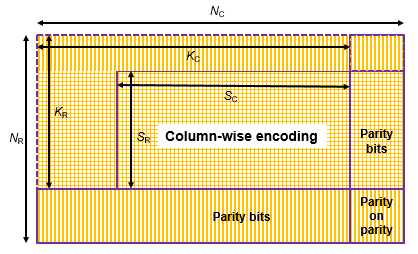
Full-length input messages are encoded using specified 2-D TPC code pairs. Row-wise encoding uses the (NC,KC) code pair and column-wise encoding uses the (NR,KR) code pair. The input vector length must be KR · KC. The input message bits vector is arranged into a KR-by-KC matrix.
Row-wise encoding uses an (NC,KC) systematic linear block encoder with KC bits per row. The row-wise encoding results in a KR-by-NC matrix that includes parity bits added to each row.
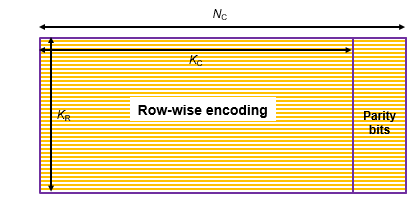
Next, column-wise encoding uses an (NR,KR) systematic linear block encoder on each of the NC columns. Applying this 2-D TPC encoding to the initial KR-by-KC matrix results in an NR-by-NC matrix that includes parity bits added to each row and column.

The 2-D TPC full-code matrix is reshaped into a column vector of length NR · NC and returned as the TPC-encoded output.
 Construction of Shortened Message Product Codes
Construction of Shortened Message Product Codes
Shortened input messages are encoded using specified 2-D TPC code pairs. Row-wise encoding uses the (NC,KC) code pair and column-wise encoding uses an (NR,KR) code pair. The input vector length must be SR · SC. The input shortened message bits vector is arranged into an SR-by-SC matrix. The shortened message matrix prepends two dimensions by padding the beginning of the message matrix with zeros. The resulting matrix is a KR-by-KC matrix.
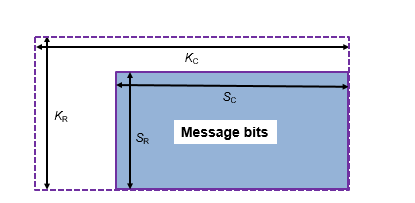
Row-wise encoding uses an (NC,KC) systematic linear block encoder with KC bits per row. The row-wise encoding results in a KR-by-NC matrix that includes parity bits added to each row.

Next, the column-wise encoding uses an (NR,KR) systematic linear block encoder on each of the NC columns.
Applying this 2-D TPC encoding to the initial KR-by-KC matrix and excluding the zero-padded bits from the output results in an (NR–KR+SR)-by-(NC–KC+SC) matrix. This matrix includes parity bits added to each row and column.
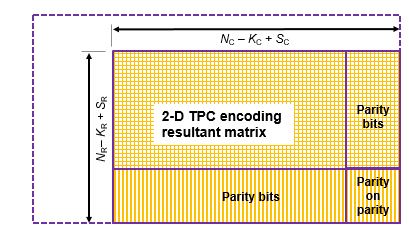
The 2-D TPC shortened-code matrix is reshaped into a column vector of length (NR–KR+SR) · (NC–KC+SC) and returned as the TPC-encoded output.
References
[1] Pyndiah, R. M. "Near-Optimum Decoding of Product Codes: Block Turbo Codes." IEEE Transactions on Communications. Vol. 46, Number 8, August 1998, pp. 1003–1010.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2018b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)