For this example, consider a structural model that consists of two square plates connected with pillars at each vertex as depicted in the figure below. The lower plate is attached rigidly to the ground while the pillars are attached rigidly to each vertex of the square plate.
Load the finite element model matrices contained in platePillarModel.mat and create the sparse second-order model representing the above system.
Use showStateInfo to examine the components of the mechss model object.
The state groups are:
Type Name Size
----------------------------
Component Plate1 2646
Component Plate2 2646
Component Pillar3 132
Component Pillar4 132
Component Pillar5 132
Component Pillar6 132
Now, load the interfaced degree of freedom (DOF) index data from dofData.mat and use interface to create the physical connections between the two plates and the four pillars. dofs is a 6x7 cell array where the first two rows contain DOF index data for the first and second plates while the remaining four rows contain index data for the four pillars. By default, the function uses dual-assembly method of physical coupling.
Specify connection between the bottom plate and the ground.
Use showStateInfo to confirm the physical interfaces.
The state groups are:
Type Name Size
-----------------------------------
Component Plate1 2646
Component Plate2 2646
Component Pillar3 132
Component Pillar4 132
Component Pillar5 132
Component Pillar6 132
Interface Plate1-Pillar3 12
Interface Plate2-Pillar3 12
Interface Plate1-Pillar4 12
Interface Plate2-Pillar4 12
Interface Plate1-Pillar5 12
Interface Plate2-Pillar5 12
Interface Plate1-Pillar6 12
Interface Plate2-Pillar6 12
Interface Plate2-Ground 6
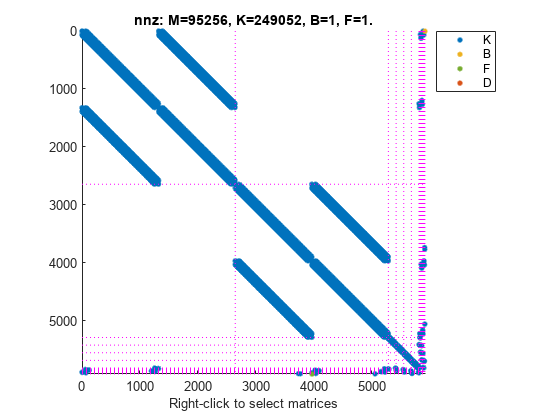
You can use spy to visualize the sparse matrices in the final model.
Now, specify physical connections using the primal-assembly method.
Use showStateInfo to confirm the physical interfaces.
The state groups are:
Type Name Size
----------------------------
Component Plate1 2646
Component Plate2 2640
Component Pillar3 108
Component Pillar4 108
Component Pillar5 108
Component Pillar6 108
Primal assembly eliminates half of the redundant DOFs associated with the shared set of DOFs in the global finite element mesh.
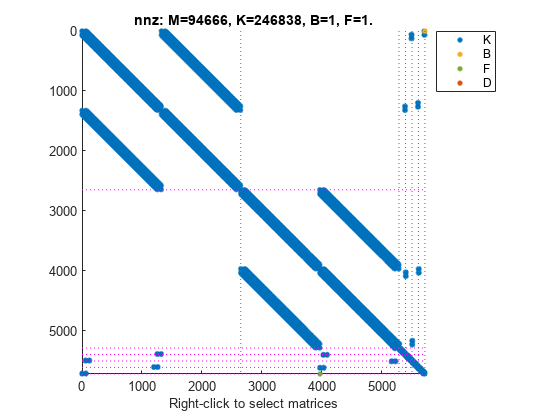
You can use spy to visualize the sparse matrices in the final model.
The data set for this example was provided by Victor Dolk from ASML.