Define Custom Deep Learning Operations
Tip
This topic explains how to define custom deep learning operations for your problems. For a list of built-in layers for neural networks, see List of Deep Learning Layers. For a list of functions that support custom layers and deep learning models defined as functions, see List of Functions with dlarray Support.
When you define a custom loss function, custom layer forward function, or define a deep
learning model as a function, if the software does not provide the deep learning operation
that you require for your task, then you can define your own function using
dlarray objects. For more information, see Define Custom Operation as MATLAB Function.
Most deep learning workflows use gradients to train the model. If the function only uses functions that support dlarray objects, then you can use the functions directly and the software determines the gradients automatically using automatic differentiation. For example, you can pass dlarray object functions like crossentropy to as a loss function to the trainnet function, or use dlarray object functions like dlconv in custom layer functions. For a list of functions that support dlarray objects, see List of Functions with dlarray Support.
If you want to use functions that do not support dlarray objects, or want
to use a specific algorithm to compute the gradients, then you can define a custom deep
learning operation as a differentiable function object. For more information, see Define Custom Operation as DifferentiableFunction Object
Deep Learning Operation Architecture
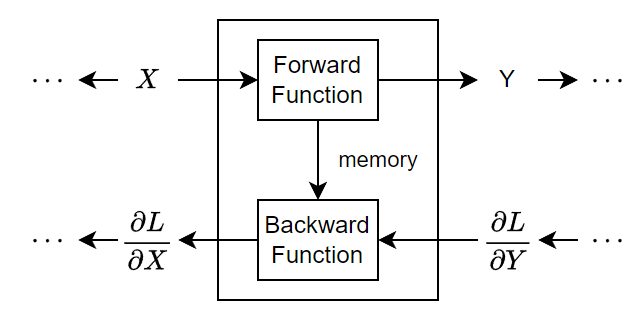
During training, the software iteratively performs forward and backward passes through the deep learning model.
During a forward pass through the model, each operation takes the outputs of the previous operations and any additional parameters (including learnable and state parameters), applies a function, and then outputs (forward propagates) the results and any update state parameters to the next operations.
Deep learning operations can have multiple inputs or outputs. For example, an operation can take X1, …, XN from multiple previous operations and forward propagate the outputs Y1, …, YM to subsequent operations.
At the end of a forward pass of the deep learning model, the software calculates the loss L between the predictions and the targets.
During the backward pass through the model, each operation takes the derivatives of the loss with respect to the outputs of the operation, computes the derivatives of the loss L with respect to the inputs, and then backward propagates the results. The software uses these derivatives to update the learnable parameters. To save on computation, the forward function can share information with the backward function using an optional memory output.
This figure illustrates the flow of data through a deep learning operation and highlights the data flow through an operation with a single input X and a single output Y.
Define Custom Operation as MATLAB Function
Define a function in MATLAB® for dlarray objects.
For example, to create a function that applies the SReLU operation, use:
function Y = srelu(X,tl,al,tr,ar) % Y = srelu(X,tl,al,tr,ar) applies the SReLU operation to the input % data X using the specified left threshold and slope tl and al, % respectively, and the right threshold and slope tr and ar, % respectively. Y = (X <= tl) .* (tl + al.*(X-tl)) ... + ((tl < X) & (X < tr)) .* X ... + (tr <= X) .* (tr + ar.*(X-tr)); end
Because the function fully supports dlarray objects, the function
supports automatic differentiation. Support for automatic differentiation enables you to
use this function as part of custom loss functions, custom layer functions, deep
learning models defined as functions.
You can use the function in custom loss functions, custom layer functions and deep learning models defined as functions. For example, to evaluate the function on random data, use:
X = rand([224 224 3 128]); Y = srelu(X);
Define Custom Operation as DifferentiableFunction Object
If you want to use functions that do not support dlarray objects, or
want to use a specific algorithm to compute the gradients, then you can define a custom
deep learning function.
Custom Operation Template
To define a custom deep learning operation, use this class definition template. This template gives the structure of a custom operation class definition. It outlines:
The optional
propertiesblock for the operation properties.The constructor function.
The
forwardfunction.The
backwardfunction.
classdef myFunction < deep.DifferentiableFunction properties % (Optional) Operation properties. % Declare operation properties here. end methods function fcn = myFunction % Create a myFunction. % This function must have the same name as the class. fcn@deep.DifferentiableFunction(numOutputs, ... SaveInputsForBackward=tf, ... SaveOutputsForBackward=tf, ... NumMemoryValues=K); end function [Y,memory] = forward(fcn,X) % Forward input data through the function and output the result % and a memory value. % % Inputs: % fcn - Function object to forward propagate through % X - Function input data % Outputs: % Y - Output of function forward function % memory - (Optional) Memory value for backward % function % % - For functions with multiple inputs, replace X with % X1,...,XN, where N is the number of inputs. % - For functions with multiple outputs, replace Y with % Y1,...,YM, where M is the number of outputs. % - For functions with multiple memory outputs, replace % memory with memory1,...,memoryK, where K is the % number of memory outputs. % Define forward function here. end function dLdX = backward(fcn,dLdY,computeGradients,X,Y,memory) % Backward propagate the derivative of the loss function % through the function. % % Inputs: % fcn - Function object to backward % propagate through % dLdY - Derivative of loss with respect to % function output % computeGradients - Logical flag indicating whether to % compute gradients % X - (Optional) Function input data % Y - (Optional) Function output data % memory - (Optional) Memory value from % forward function % Outputs: % dLdX - Derivative of loss with respect to function % input % % - For functions with multiple inputs, replace X and dLdX % with X1,...,XN and dLdX1,...,dLdXN, respectively, where N % is the number of inputs. In this case, computeGradients is % a logical vector of size N, where non-zero elements % indicate to compute gradients for the corresponding input. % - For functions with multiple outputs, replace Y and dLdY % with Y1,...,YM and dLdY,...,dLdYM, respectively, where M % is the number of outputs. % Define backward function here. end end end
Forward Function
The forward function defines the deep learning forward pass operation. It
has the syntax [Y,memory] = forward(~,X). The function has these inputs
and outputs:
X— Operation input data.Y— Operation output data.memory(optional) — Memory value for the backward function. To avoid repeated calculations in the backward function, use this output to share data with the backward function. To use memory values, set theNumMemoryValuesargument ofdeep.DifferentiableFunctionin the constructor function to a positive integer.
You can adjust the syntax for operations with multiple inputs, outputs, and memory values:
For operations with multiple inputs, replace
XwithX1,...,XN, whereNis the number of inputs.For operations with multiple outputs, replace
YwithY1,...,YM, whereMis the number of outputs.For operations with multiple memory values, replace
memorywithmemory1,...,memoryK, whereKis the number of memory values.
Tip
If the number of inputs to the operation can vary, then use varargin
instead of X1,…,XN. In this case, varargin is a
cell array of the inputs, where varargin{i} corresponds to
Xi.
Backward Function
The backward function defines the operation backward function. It has the syntax dLdX = backward(fcn,dLdY,computeGradients,X,Y,memory). The function has these inputs and output:
fcn— Differentiable function object to backward propagate through.dLdY— Gradients of the loss with respect to the operation output dataY.computeGradients— Logical flag indicating to compute gradients for the input, specified as1(true) or0(false).X(optional) — Operation input data. To use the operation input data, set theSaveInputsForBackwardargument ofdeep.DifferentiableFunctionin the constructor function to1(true).Y(optional) — Operation output data. To use the operation output data, set theSaveOutputsForBackwardargument ofdeep.DifferentiableFunctionin the constructor function to1(true).memory(optional) — Memory value from the forward function. To use memory values, set theNumMemoryValuesargument ofdeep.DifferentiableFunctionin the constructor function to a positive integer.dLdX— Gradients of the loss with respect to the operation input dataX.
The values of X and Y are the same as in the forward function. The dimensions of dLdY are the same as the dimensions of Y.
The dimensions and data type of dLdX are the same as the dimensions and data type of X.
You can adjust the syntaxes for operations with multiple inputs, and multiple outputs:
For operations with multiple inputs, replace
XanddLdXwithX1,...,XNanddLdX1,...,dLdXN, respectively, whereNis the number of inputs. In this case,computeGradientsis a logical vector of sizeN, where non-zero elements indicate to compute gradients for the corresponding input.For operations with multiple outputs, replace
YanddLdYwithY1,...,YManddLdY1,...,dLdYM, respectively, whereMis the number of outputs.For operations with multiple memory outputs, replace
memorywithmemory1,...,memoryK, whereKis the number of memory values.
To reduce memory usage by preventing unused variables being saved between the forward and backward pass, replace the corresponding input arguments with ~.
Tip
If the number of inputs to backward can vary, then use varargin instead of the input arguments after fcn. In this case, varargin is a cell array of the inputs, where:
The first
Melements correspond to theM, derivativesdLdY1,...,dLdYM.The next element corresponds to
computeGradients.The next
Nelements correspond to theNinputsX1,...,XN.The next
Melements correspond to theMoutputsY1,...,YM.The remaining elements correspond to the memory values.
To calculate the derivatives of the loss with respect to the input data, you can use the chain rule with the derivatives of the loss with respect to the output data and the derivatives of the output data with respect to the input data.:
Create Interface Function
After you create an instance of differentiable function object, you can use
evaluate the object as if it were a MATLAB function. To make it easier to include the function along side other
dlarray object functions, create a function that takes
dlarray objects as input and returns dlarray
objects. Inside this function create and configure the differentiable function
object and evaluate it.
For example, to create a custom SReLU function, that creates and evaluates a differentiable function, use:
function Y = srelu(X,tl,al,tr,ar) format = dims(X); fcn = sreluFunction(format); Y = fcn(X,tl,al,tr,ar); Y = dlarray(Y,format); end
GPU Compatibility
Custom operations defined as MATLAB functions are GPU compatible; if the function fully supports
dlarray objects, then the function is GPU compatible.
For custom operations defined as DifferentiableFunction objects, if
the forward and backward functions fully support gpuArray (Parallel Computing Toolbox) objects, then the function object is GPU compatible.
Many MATLAB built-in functions support gpuArray (Parallel Computing Toolbox) and dlarray input arguments. For a list of
functions that execute on a GPU, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox). To use a GPU for deep
learning, you must also have a supported GPU device. For information on supported devices, see
GPU Computing Requirements (Parallel Computing Toolbox). For more information on working with GPUs in MATLAB, see GPU Computing in MATLAB (Parallel Computing Toolbox).
See Also
trainnet | trainingOptions | dlnetwork | functionLayer
Topics
- Specify Custom Operation Backward Function
- Train Model Using Custom Backward Function
- Define Custom Deep Learning Layers
- Specify Custom Layer Backward Function
- List of Functions with dlarray Support
- Train Network Using Model Function
- Update Batch Normalization Statistics Using Model Function
- Initialize Learnable Parameters for Model Function