Out-of-Distribution Detection for Deep Neural Networks
This example shows how to detect out-of-distribution (OOD) data in deep neural networks.
OOD data detection is the process of identifying inputs to a deep neural network that might yield unreliable predictions. OOD data refers to data that is different from the data used to train the model. For example, data collected in a different way, at a different time, under different conditions, or for a different task than the data on which the model was originally trained.
By assigning confidence scores to the predictions of a network, you can classify data as in-distribution (ID) or OOD. You can then choose how you treat OOD data. For example, you can choose to reject the prediction of a neural network if it detects OOD data.
This example requires the Deep Learning Toolbox™ Verification Library. To download and install the support package, use the Add-On Explorer. Alternatively, see Deep Learning Toolbox Verification Library.
Load Data
This example uses MATLAB® files converted by MathWorks® from the Tennessee Eastman Process (TEP) simulation data [1]. These files are available at the MathWorks support files site. For more information, see the disclaimer: https://www.mathworks.com/supportfiles/predmaint/chemical-process-fault-detection-data/Disclaimer.txt.
Download the training and test files. Depending on your internet connection, the download process can take a long time.
faultfreetrainingFileName = matlab.internal.examples.downloadSupportFile("predmaint","chemical-process-fault-detection-data/faultfreetraining.mat"); faultfreetestingFileName = matlab.internal.examples.downloadSupportFile("predmaint","chemical-process-fault-detection-data/faultfreetesting.mat"); faultytrainingFileName = matlab.internal.examples.downloadSupportFile("predmaint","chemical-process-fault-detection-data/faultytraining.mat"); faultyttestingFileName = matlab.internal.examples.downloadSupportFile("predmaint","chemical-process-fault-detection-data/faultytesting.mat");
Load the downloaded files into the MATLAB workspace. For more information about this data set, see Chemical Process Fault Detection Using Deep Learning.
load(faultfreetrainingFileName); load(faultfreetestingFileName); load(faultytrainingFileName); load(faultyttestingFileName);
The data set consists of four MAT files: fault-free training, fault-free testing, faulty training, and faulty testing.
The fault-free training and testing data sets each comprise 500 simulations of fault-free data. Each fault-free simulation has 52 channels and the class label 0.
The faulty training and testing data sets each comprise 10,000 simulations corresponding to 500 simulations for each of 20 possible faults. Simulations 1–500 correspond to class label 1, simulations 501–1000 correspond to class label 2, and so on. Each simulation has 52 channels.
The length of each simulation depends on the data set. All simulations were sampled every three minutes.
Each simulation in the training data sets contains 500 time samples from 25 hours of simulation.
Each simulation in the testing data sets contains 960 time samples from 48 hours of simulation.
Load Pretrained Network
Load a pretrained network. This network has been trained using the training method from the Chemical Process Fault Detection Using Deep Learning example. Because of the randomness of training, if you train this network yourself, you will likely see different results.
load("trainedFaultDetectionNetwork.mat","net","classNames");
Preprocess Data
Remove data entries with the fault class labels 3, 9, and 15 in the training and testing data sets. These faults are not present in the original training data set. Because the model was not trained using these faults, they are OOD inputs to the network.
Use the supporting function helperPrepareDataSets to prepare the data sets for training and testing. The function performs these steps:
Combine the fault-free data, corresponding to class label 0, with the faulty data, corresponding to class labels 1-20.
Hold-out the simulations for faults 3, 9, and 15.
Normalize the data.
Create an array of class labels.
Process the training and test data sets.
classesToRemove = [3 9 15]; [XTrain,XTrainHoldOut,TTrain,TTrainHoldOut] = helperPrepareDataSets(faultfreetraining,faultytraining,classesToRemove); [XTest,XTestHoldOut,TTest,TTestHoldOut] = helperPrepareDataSets(faultfreetesting,faultytesting,classesToRemove);
Visualize Data
The XTrain and XTest data sets each contain 500 fault-free simulations followed by 8500 faulty simulations corresponding to 500 simulations for each of the 17 faults in the training set. Visualize the fault-free and faulty training data for four of the 52 channels.
numChannelsToPlot = 4;
Plot an example of fault-free data. The first 500 simulations correspond to the fault-free data.
figure
tiledlayout(2,1)
nexttile
plot(XTrain{1}(1:numChannelsToPlot,:)')
xlabel("Time Step");
title("Fault-Free Data (Class 0)")
legend("Channel " + string(1:numChannelsToPlot),Location="northeastoutside")Plot an example of faulty data. Simulations 501–1000 correspond to data with fault 1.
nexttile
plot(XTrain{501}(1:numChannelsToPlot,:)')
xlabel("Time Step")
title("Faulty Data (Class 1)")
legend("Channel " + string(1:numChannelsToPlot),Location="northeastoutside")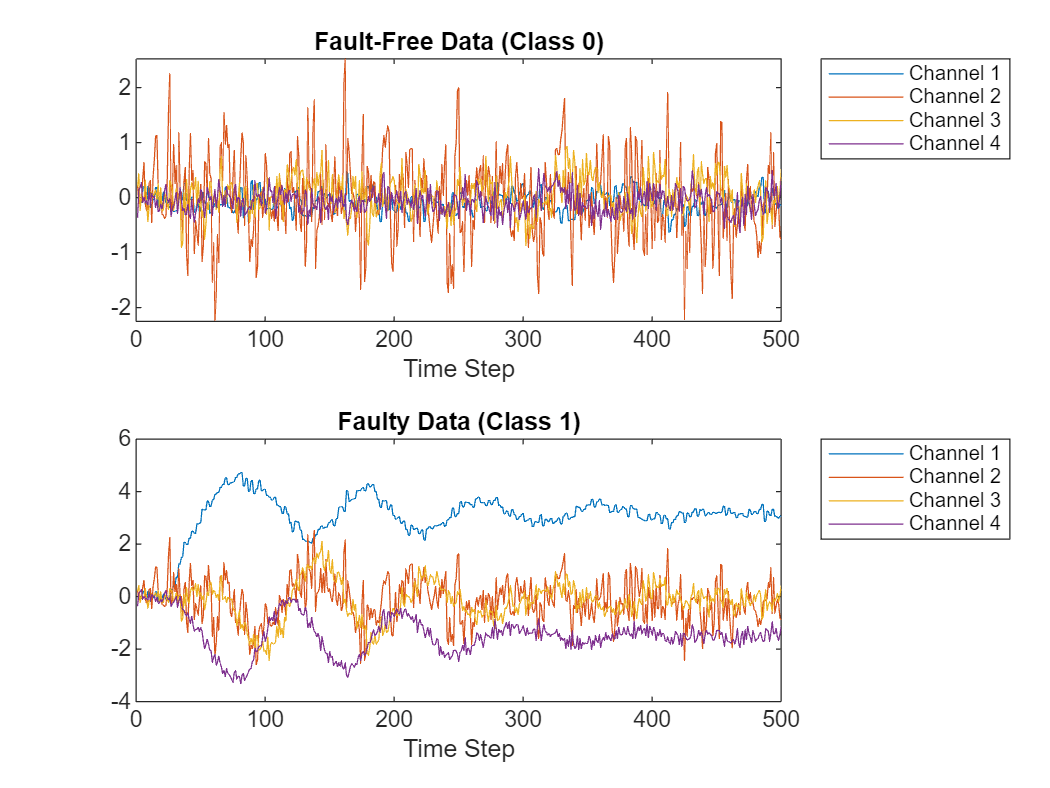
Test Network
Test the trained network by classifying the fault type for each of the test observations. To make predictions with multiple observations, use the minibatchpredict function. Convert the classification scores to class labels using the scores2label function. The minibatchpredict function automatically uses a GPU if one is available. Using a GPU requires a Parallel Computing Toolbox™ license and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox). Otherwise, the function uses the CPU.
Because the data has sequences with rows and columns corresponding to channels and time steps, respectively, specify the input data format "CTB" (channel, time, batch).
scores = minibatchpredict(net,XTest,InputDataFormats="CTB");
YPred = scores2label(scores,classNames);Calculate the accuracy.
acc = sum(YPred == TTest)/numel(YPred)
acc = 0.9988
Plot the confusion matrix using the true class labels and the predicted labels.
figure confusionchart(TTest,YPred)

Test the trained network on the held-out data.
scores = minibatchpredict(net,XTestHoldOut,InputDataFormats="CTB");
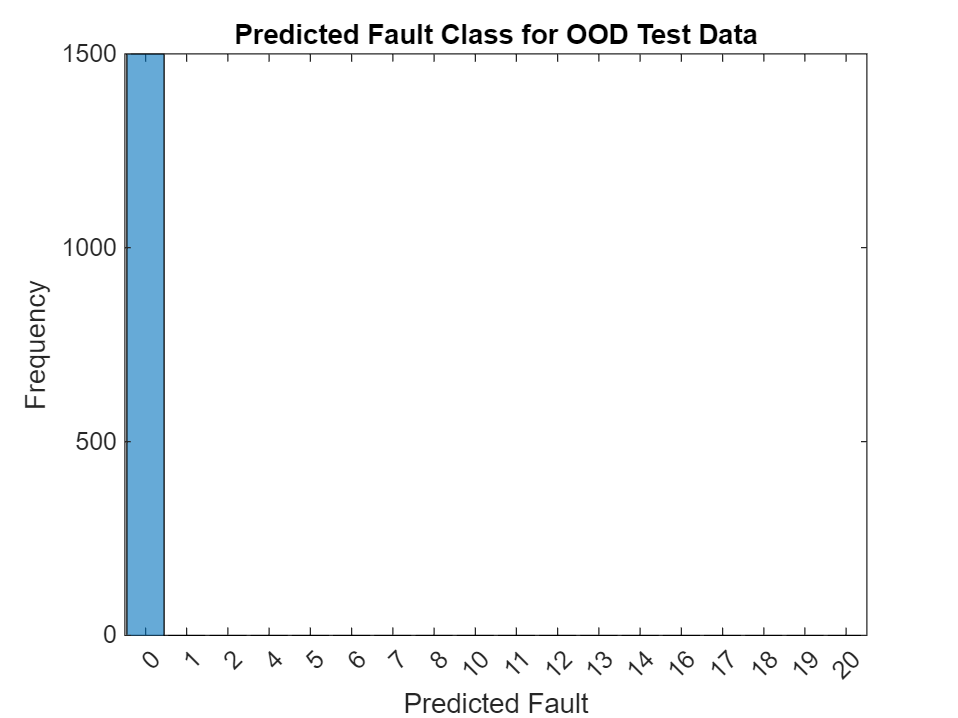
YPredHoldOut = scores2label(scores,classNames);Plot the predicted class labels for the held-out data. The network must predict the class of the held-out data as one of the classes on which it was trained. Here, the network predicts class 0 (fault-free) for all of the held-out test observations. Because the network was not trained using these fault labels, it cannot classify the faults correctly. Therefore, the network predicts "fault-free" even though the data is faulty.
figure histogram(YPredHoldOut) xlabel("Predicted Fault") ylabel("Frequency") title("Predicted Fault Class for OOD Test Data")
Analyze Softmax Scores
The data set contains two types of data:
In-distribution (ID) — Data used to train the network. This data corresponds to faults with class labels 0, 1, 2, 4–8,10–14, and 16–20.
Out-of-distribution (OOD) — Data that is different from the training data, for example, the data corresponding to faults 3, 9, and 15. The network cannot classify this type of data reliably.
You can use OOD detection to assign a confidence score to the network predictions. A lower confidence value corresponds to data that is more likely to be OOD.
In this example, you assign confidence scores to network predictions by using the softmax probabilities to compute a distribution confidence score for each observation. ID data usually has a higher maximum softmax probability than OOD data [2]. You can then apply a threshold to the softmax probabilities to determine whether an input is ID or OOD. This technique is called the baseline method.
Compute the maximum softmax scores for each observation in the training data sets.
scoreTraining = max(minibatchpredict(net,XTrain,InputDataFormats="CTB"),[],2); scoreTrainingHoldOut = max(minibatchpredict(net,XTrainHoldOut,InputDataFormats="CTB"),[],2);
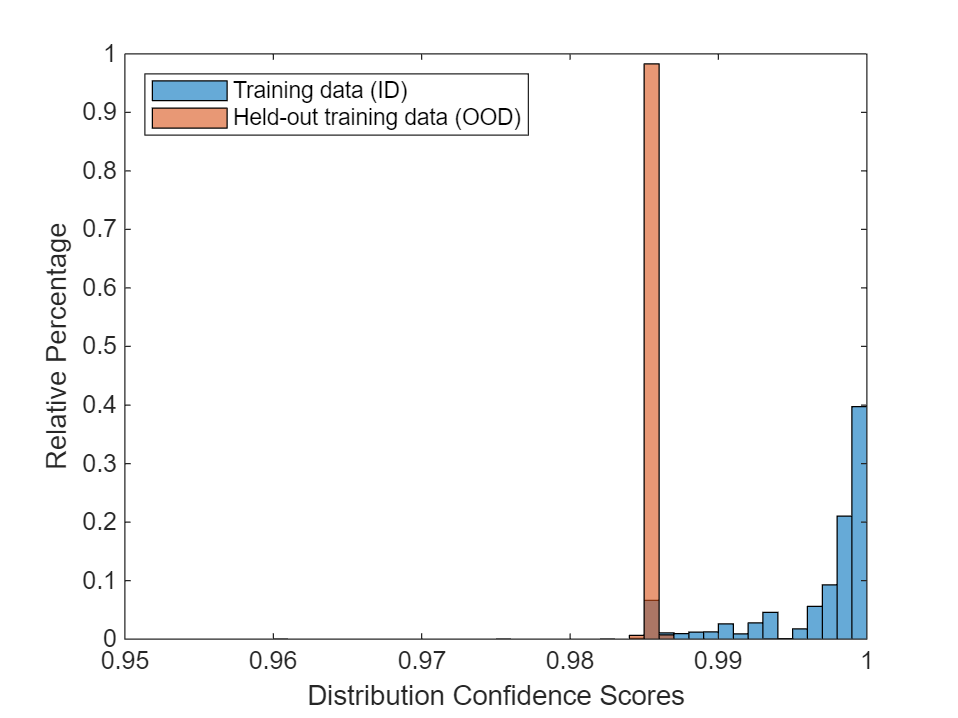
Plot histograms of the scores for the ID data (scoreTraining) and the OOD data (scoreTrainingHoldOut). To compare the distributions, set the histogram normalization to "probability". The plot shows a clear separation between the distribution confidence scores for the ID and OOD data. A threshold of around 0.99 reliably separates the scores of the ID and OOD observations.
figure binWidth = 0.001; histogram(scoreTraining,Normalization="probability",BinWidth=binWidth) hold on histogram(scoreTrainingHoldOut,Normalization="probability",BinWidth=binWidth) hold off xlim([0.95 1]); legend("Training data (ID)", "Held-out training data (OOD)",Location="northwest") xlabel("Distribution Confidence Scores") ylabel("Relative Percentage")
Out-of-Distribution Detection
You can use the isInNetworkDistribution function to determine whether an observation is ID or OOD. The function takes as input a network, data, and a threshold. The function uses the maximum softmax scores to find the distribution confidence scores and the specified threshold to classify data as ID or OOD.
The isInNetworkDistribution function requires the data as a formatted dlarray object or a minibatchqueue object that returns a dlarray. Convert the data to a formatted dlarray object using the convertDataToDlarray supporting function, found at the end of this example.
XTrain = convertDataToDlarray(XTrain); XTrainHoldOut = convertDataToDlarray(XTrainHoldOut); XTest = convertDataToDlarray(XTest); XTestHoldOut = convertDataToDlarray(XTestHoldOut);
Manual Threshold
You can use the histogram of the softmax scores to manually choose a threshold that visually separates the maximum softmax scores in the training data set. This process is called OOD data discrimination.
Use the threshold to classify the test data as ID or OOD. The isInNetworkDistribution function returns a logical 1 (true) for each observation with maximum softmax above the specified threshold, corresponding to that observation being classified as ID.
threshold = 0.99; tfID = isInNetworkDistribution(net,XTest,Threshold=threshold); tfOOD = isInNetworkDistribution(net,XTestHoldOut,Threshold=threshold);
You can test the performance of the OOD data discriminator by calculating the true positive rate (TPR) and the false positive rate (FPR).
TPR — Proportion of ID observations correctly classified as ID.
FPR — Proportion of OOD observations incorrectly classified as ID.
Compute the TPR and FPR using the helperPredictionMetrics helper function. A good discriminator has a TPR close to 1 and a FPR close to 0.
[TPR,FPR] = helperPredictionMetrics(tfID,tfOOD)
TPR = 0.8818
FPR = 0
Optimal Threshold
Rather than manually selecting a threshold, you can use the threshold that best separates the softmax scores. You can find the optimal threshold by maximizing the TPR and minimizing the FPR. Create a distribution discriminator object using the networkDistributionDiscriminator function. You can use this object to find the optimal threshold.
Use the networkDistributionDiscriminator function with the network as input. Use the training data as ID data and the held-out training data as OOD data. Set the method input to "baseline" to use the maximum softmax scores as the distribution confidence scores. The discriminator determines the optimal threshold.
method = "baseline";
discriminatorOptimized = networkDistributionDiscriminator(net,XTrain,XTrainHoldOut,method)discriminatorOptimized =
BaselineDistributionDiscriminator with properties:
Method: "baseline"
Network: [1×1 dlnetwork]
Threshold: 0.9861
Use the distribution discriminator to classify the test data as ID or OOD.
tfIDOptimized = isInNetworkDistribution(discriminatorOptimized,XTest); tfOODOptimized = isInNetworkDistribution(discriminatorOptimized,XTestHoldOut);
Compute the TPR and FPR using the optimized threshold.
[TPROptimized,FPROptimized] = helperPredictionMetrics(tfIDOptimized,tfOODOptimized)
TPROptimized = 0.9251
FPROptimized = 6.6667e-04
Threshold for Specified True Positive Goal
You can set a target number of true positives at the expense of a greater number of false positives. Set a true positive goal of 95% and use the training data to find a threshold. Again, use the distribution discriminator to classify the test data as ID or OOD and examine the TPR and FPR for the test set.
discriminatorTPR = networkDistributionDiscriminator(net,XTrain,XTrainHoldOut,method,TruePositiveGoal=0.95); tfIDTPR = isInNetworkDistribution(discriminatorTPR,XTest); tfOODTPR = isInNetworkDistribution(discriminatorTPR,XTestHoldOut); [TPROptimizedTPR,FPROptimizedTPR] = helperPredictionMetrics(tfIDTPR,tfOODTPR)
TPROptimizedTPR = 0.9464
FPROptimizedTPR = 0.3040
Compare Discriminators
Use the helperDistributionConfusionMatrix helper function to plot the confusion matrix resulting from the predictions using each of the three threshold choices.
figure tiledlayout(2,2) nexttile helperDistributionConfusionMatrix(tfID,tfOOD); title("Manual Threshold") nexttile helperDistributionConfusionMatrix(tfIDOptimized,tfOODOptimized); title("Optimal Threshold (TPR & FPR)") nexttile helperDistributionConfusionMatrix(tfIDTPR,tfOODTPR); title("Threshold (TPR of 0.95)")

Plot ROC Curve
The distribution discriminator object is a binary classifier that uses a threshold to classify network predictions as ID or OOD. Plot the receiver operating characteristic (ROC) curve for this binary classifier to see the trade-off between true positive and false positive rates. The ROC curve represents every possible threshold. Add a point to the curve highlighting each threshold value.
scoresID = distributionScores(discriminatorOptimized,XTest);
scoresOOD = distributionScores(discriminatorOptimized,XTestHoldOut);
numObservationsID = size(scoresID,1);
numObservationsOOD = size(scoresOOD,1);
scores = [scoresID',scoresOOD'];
trueDataLabels = [
repelem("In-Distribution",numObservationsID), ...
repelem("Out-of-Distribution",numObservationsOOD)];
rocObj = rocmetrics(trueDataLabels,scores,"In-Distribution");
figure
plot(rocObj,ShowModelOperatingPoint=false)
hold on
plot(FPR,TPR,".", ...
MarkerSize=20, ...
DisplayName="Manual Threshold")
plot(FPROptimized,TPROptimized,".", ...
MarkerSize=20, ...
DisplayName="Optimal Threshold")
plot(FPROptimizedTPR,TPROptimizedTPR,".", ...
MarkerSize=20, ...
DisplayName="Threshold at TPR=0.95")
Verify Network Predictions
You can use the distribution discriminator object to add an extra level of verification to network predictions. For example, for every prediction that the network makes, the distribution discriminator can confirm whether to reject the result based on the input classification. If the distribution discriminator determines that the input is OOD, then you can reject the result.
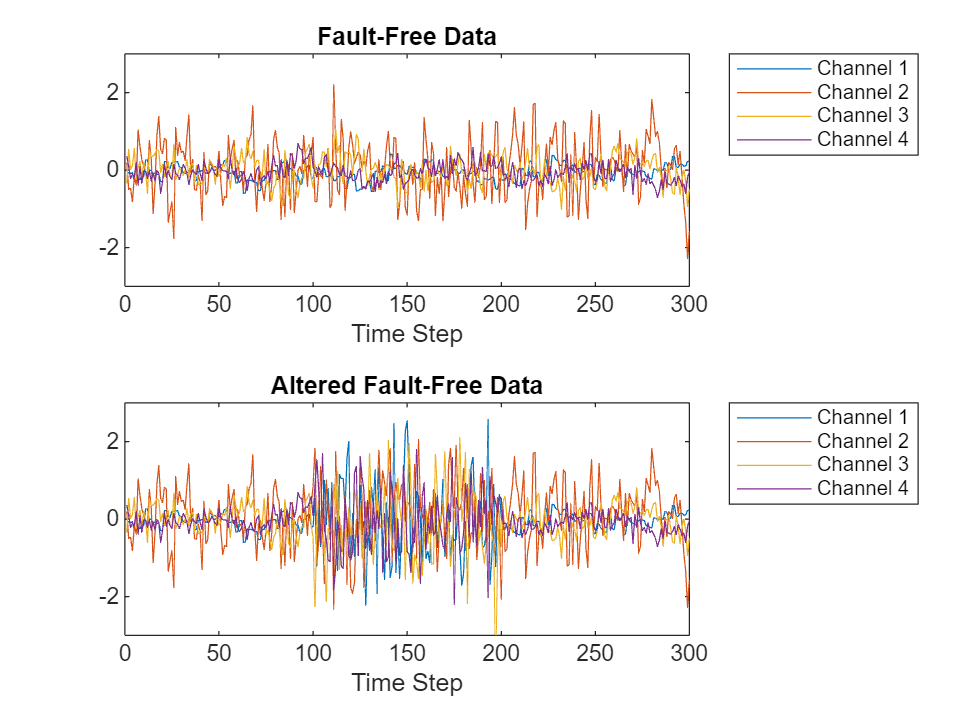
Suppose that a silent, temporary failure in the system alters a single fault-free simulation such that the data contains white noise from timestep 101-200.
rng("default")
faultfreetestingSample = extractdata(squeeze(XTest(:,1,:)));
alteredFaultFreeSignal = faultfreetestingSample;
alteredFaultFreeSignal(:,101:200) = randn(52,100);Plot the first 300 timesteps of the original fault-free signal and an altered fault-free signal for four of the 52 channels.
figure tiledlayout(2,1) nexttile plot(faultfreetestingSample(1:4, 1:300)') ylim([-3 3]) xlabel("Time Step"); title("Fault-Free Data") legend("Channel " + string(1:4),Location="northeastoutside") nexttile plot(alteredFaultFreeSignal(1:4, 1:300)') ylim([-3 3]) xlabel("Time Step") title("Altered Fault-Free Data") legend("Channel " + string(1:4),Location="northeastoutside")
Classify the altered fault-free signal. To make predictions with a single observation, use the predict function. To use a GPU, first convert the data to gpuArray.
dlbrokenFaultFreeSignal = dlarray(alteredFaultFreeSignal,'CTB'); if canUseGPU dlbrokenFaultFreeSignal = gpuArray(dlbrokenFaultFreeSignal); end scores = predict(net,dlbrokenFaultFreeSignal); Ypredi = scores2label(scores,classNames)
Ypredi = categorical
0
The network still classifies the altered signal as class label 0, which corresponds to "fault-free". However, this altered signal is from a different distribution than the data that the network sees during training and the classification must be flagged in a safety-critical system.
Use the discriminator to determine whether the signal is ID or OOD. Use the isInNetworkDistribution function to test if the observation is ID.
tf = isInNetworkDistribution(discriminatorOptimized,dlbrokenFaultFreeSignal)
tf = gpuArray logical 0
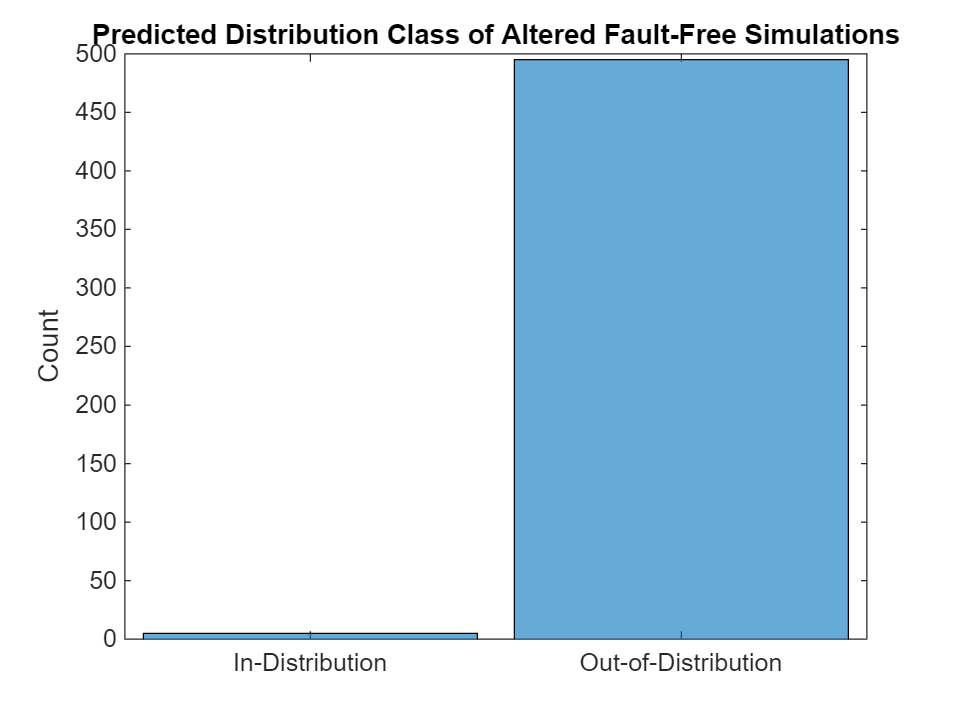
Apply the same alteration to all 500 fault-free signals and analyze the number of OOD samples detected. The discriminator successfully picks up this new fault and classifies most of the altered simulations as OOD.
alteredFaultFreeSignals = XTest(:,1:500,:); alteredFaultFreeSignals(:,:,101:200) = randn(52,500,100); tf = isInNetworkDistribution(discriminatorOptimized,alteredFaultFreeSignals); figure YPredAltered = repelem("Out-of-Distribution",length(tf)); YPredAltered(tf == 1) = "In-Distribution"; histogram(categorical(YPredAltered)) ylabel("Count") title("Predicted Distribution Class of Altered Fault-Free Simulations")
Helper Functions
helperNormalizeData
The helperNormalizeData function normalizes the data using the same statistics as the training data.
function processed = helperNormalizeData(data) limit = max(data.sample); processed = helperPreprocess(data{:,:},limit); % The network requires the input data to be normalized with respect to the training % data. Loading the training data and computing these statistics is % computationally expensive, so load precalculated statistics. s = load("faultDetectionNormalizationStatistics.mat","tMean","tSigma"); processed = helperNormalize(processed,s.tMean,s.tSigma); end
helperPreprocess
The helperPreprocess function uses the maximum sample number to preprocess the data. The sample number indicates the signal length, which is consistent across the data set. The function uses a for-loop to go over the data set with a signal length filter to form sets of 52 signals. Each set is an element of a cell array. Each cell array contains data from a single simulation.
function processed = helperPreprocess(data,limit) H = size(data,1); processed = {}; for ind = 1:limit:H x = data(ind:(ind+(limit-1)),4:end); processed = [processed; x']; end end
helperNormalize
The helperNormalize function uses the mean and standard deviation of the training data to normalize data.
function data = helperNormalize(data,m,s) for ind = 1:size(data,1) data{ind} = (data{ind} - m)./s; end end
helperPrepareDataSets
The helperPrepareDataSets function prepares the data set for analysis. The function takes as input the fault-free data, the faulty data, and the faults to be removed. The function returns the faulty data with the specified classes removed, the removed data, and the associated labels for both data sets. This is the same data processing performed before training.
function[dataProcessed,dataHoldOut,labels,labelsHoldOut] = helperPrepareDataSets(faultFreeData,faultyData,classesToRemove) index = ismember(faultyData.faultNumber,classesToRemove); data = [faultFreeData; faultyData(~index,:)]; dataHoldOut = faultyData(index,:); dataProcessed = helperNormalizeData(data); dataHoldOut = helperNormalizeData(dataHoldOut); classesToKeep = 1:20; classesToKeep = classesToKeep(~ismember(classesToKeep,classesToRemove)); labels = categorical([zeros(500,1); repmat(classesToKeep,1,500)']); labelsHoldOut = categorical(repmat(classesToRemove,1,500)'); end
convertDataToDlarray
The convertDataToDlarray function converts the data to a dlarray object.
function dldata = convertDataToDlarray(data) % Reshape the data. dataSize = size(data,1); dldata = reshape(data,1,1,dataSize); % Convert the cell arrays to 3-D numeric arrays. dldata = cell2mat(dldata); % Convert the cell arrays to a dlarray object with data format labels. dldata = dlarray(dldata,"CTB"); end
helperDistributionConfusionMatrix
The helperDistributionConfusionMatrix function computes the confusion matrix for ID and OOD data. The function takes as input an array of logical values for the ID data and OOD data. A value of 1 (true) corresponds to the detector predicting that the observation is ID. A value of 0 (false) corresponding to the detector predicting that the observation is OOD.
function cm = helperDistributionConfusionMatrix(tfID,tfOOD) trueDataLabels = [ repelem("ID",numel(tfID)), ... repelem("OOD",numel(tfOOD))]; predDataLabelsID = repelem("OOD",length(tfID)); predDataLabelsID(tfID == 1) = "ID"; predDataLabelsOOD = repelem("OOD",length(tfOOD)); predDataLabelsOOD(tfOOD == 1) = "ID"; predDataLabels = [predDataLabelsID,predDataLabelsOOD]; cm = confusionchart(trueDataLabels,predDataLabels); end
helperPredictionMetrics
The helperPredictionMetrics function computes the true positive rate and false positive rate for a binary classifier.
function [truePositiveRate,falseNegativeRate] = helperPredictionMetrics(tfID,tfOOD) truePositiveRate = sum(tfID)/(sum(tfID)+sum(1-tfID)); falseNegativeRate = sum(tfOOD)/(sum(tfOOD) + sum(1-tfOOD)); end
References
[1] Rieth, C. A., B. D. Amsel, R. Tran., and B. Maia. "Additional Tennessee Eastman Process Simulation Data for Anomaly Detection Evaluation." Harvard Dataverse, Version 1, 2017. https://doi.org/10.7910/DVN/6C3JR1.
[2] Hendrycks, Dan, and Kevin Gimpel. A Baseline for Detecting Misclassified and Out of Distribution Examples in Neural Networks." arXiv:1610.02136 [cs.NE], October 3, 2018, https://arxiv.org/abs/1610.02136.
See Also
dlnetwork | dlarray | isInNetworkDistribution | networkDistributionDiscriminator | verifyNetworkRobustness | rocmetrics
Topics
- Verification of Neural Networks
- Verify Robustness of Deep Learning Neural Network
- Generate Untargeted and Targeted Adversarial Examples for Image Classification
- Train Image Classification Network Robust to Adversarial Examples
- Compare Deep Learning Models Using ROC Curves
- Out-of-Distribution Data Discriminator for YOLO v4 Object Detector
- Out-of-Distribution Detection for LSTM Document Classifier
- Verify an Airborne Deep Learning System