gjr
GJR conditional variance time series model
Description
Use gjr to specify a univariate GJR (Glosten, Jagannathan, and Runkle) model. The gjr function returns a gjr object specifying the functional form of a GJR(P,Q) model, and stores its parameter values.
The key components of a gjr model include the:
GARCH polynomial, which is composed of lagged conditional variances. The degree is denoted by P.
ARCH polynomial, which is composed of the lagged squared innovations.
Leverage polynomial, which is composed of lagged squared, negative innovations.
Maximum of the ARCH and leverage polynomial degrees, denoted by Q.
P is the maximum nonzero lag in the GARCH polynomial, and Q is the maximum nonzero lag in the ARCH and leverage polynomials. Other model components include an innovation mean model offset, a conditional variance model constant, and the innovations distribution.
All coefficients are unknown (NaN values) and estimable unless you specify their values using name-value pair argument syntax. To estimate models containing all or partially unknown parameter values given data, use estimate. For completely specified models (models in which all parameter values are known), simulate or forecast responses using simulate or forecast, respectively.
Creation
Description
Mdl = gjrgjr object.
Mdl = gjr(P,Q)Mdl) with a GARCH polynomial with a degree of P and ARCH and leverage polynomials each with a degree of Q. All polynomials contain all consecutive lags from 1 through their degrees, and all coefficients are NaN values.
This shorthand syntax enables you to create a template in which you specify the polynomial degrees explicitly. The model template is suited for unrestricted parameter estimation, that is, estimation without any parameter equality constraints. However, after you create a model, you can alter property values using dot notation.
Mdl = gjr(Name,Value)'ARCHLags',[1 4],'ARCH',{0.2 0.3} specifies the two ARCH coefficients in ARCH at lags 1 and 4.
This longhand syntax enables you to create more flexible models.
Input Arguments
The shorthand syntax provides an easy way for you to create model templates that are suitable for unrestricted parameter estimation. For example, to create a GJR(1,2) model containing unknown parameter values, enter:
Mdl = gjr(1,2);
GARCH polynomial degree, specified as a nonnegative integer. In the GARCH polynomial and at time t, MATLAB® includes all consecutive conditional variance terms from lag t – 1 through lag t – P.
You can specify this argument using the
gjr(P,Q) shorthand syntax only.
If P > 0, then you must specify Q as a positive integer.
Example: gjr(1,1)
Data Types: double
ARCH polynomial degree, specified as a nonnegative integer. In the ARCH polynomial and at time t, MATLAB includes all consecutive squared innovation terms (for the ARCH polynomial) and squared, negative innovation terms (for the leverage polynomial) from lag t – 1 through lag t – Q.
You can specify this argument using the
gjr(P,Q) shorthand syntax only.
If P > 0, then you must specify Q as a positive integer.
Example: gjr(1,1)
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
The longhand syntax
enables you to create models in which some or all coefficients are known. During estimation,
estimate imposes equality constraints on any known parameters.
Example: 'ARCHLags',[1 4],'ARCH',{NaN NaN} specifies a GJR(0,4) model and unknown, but nonzero, ARCH coefficient matrices at lags 1 and 4.
GARCH polynomial lags, specified as the comma-separated pair consisting of
'GARCHLags' and a numeric vector of unique positive
integers.
GARCHLags( is the lag corresponding to
the coefficient j)GARCH{. The lengths of
j}GARCHLags and GARCH must be equal.
Assuming all GARCH coefficients (specified by the GARCH property)
are positive or NaN values, max(GARCHLags)
determines the value of the P property.
Example: 'GARCHLags',[1 4]
Data Types: double
ARCH polynomial lags, specified as the comma-separated pair consisting of
'ARCHLags' and a numeric vector of unique positive
integers.
ARCHLags( is the lag corresponding to
the coefficient j)ARCH{. The lengths of
j}ARCHLags and ARCH must be equal.
Assuming all ARCH and leverage coefficients (specified by the
ARCH and Leverage properties) are positive
or NaN values, max([ARCHLags LeverageLags])
determines the value of the Q property.
Example: 'ARCHLags',[1 4]
Data Types: double
Leverage polynomial lags, specified as the comma-separated pair consisting of
'LeverageLags' and a numeric vector of unique positive
integers.
LeverageLags( is the lag corresponding
to the coefficient j)Leverage{. The
lengths of j}LeverageLags and Leverage must be
equal.
Assuming all ARCH and leverage coefficients (specified by the
ARCH and Leverage properties) are positive
or NaN values, max([ARCHLags LeverageLags])
determines the value of the Q property.
Example: 'LeverageLags',1:4
Data Types: double
Properties
You can set writable property values when you create the model object by using name-value argument syntax, or after you create the model object by using dot notation. For example, to create a GJR(1,1) model with unknown coefficients, and then specify a t innovation distribution with unknown degrees of freedom, enter:
Mdl = gjr('GARCHLags',1,'ARCHLags',1);
Mdl.Distribution = "t";This property is read-only.
GARCH polynomial degree, specified as a nonnegative integer. P is
the maximum lag in the GARCH polynomial with a coefficient that is positive or
NaN. Lags that are less than P can have
coefficients equal to 0.
P specifies the minimum number of presample conditional variances
required to initialize the model.
If you use name-value pair arguments to create the model, then MATLAB implements one of these alternatives (assuming the coefficient of the
largest lag is positive or NaN):
If you specify
GARCHLags, thenPis the largest specified lag.If you specify
GARCH, thenPis the number of elements of the specified value. If you also specifyGARCHLags, thengjrusesGARCHLagsto determinePinstead.Otherwise,
Pis0.
Data Types: double
This property is read-only.
Maximum degree of ARCH and leverage polynomials, specified as a nonnegative integer.
Q is the maximum lag in the ARCH and leverage polynomials in the
model. In either type of polynomial, lags that are less than Q can
have coefficients equal to 0.
Q specifies the minimum number of presample innovations required to
initiate the model.
If you use name-value pair arguments to create the model, then MATLAB implements one of these alternatives (assuming the coefficients of the
largest lags in the ARCH and leverage polynomials are positive or NaN):
If you specify
ARCHLagsorLeverageLags, thenQis the maximum between the two specifications.If you specify
ARCHorLeverage, thenQis the maximum number of elements between the two specifications. If you also specifyARCHLagsorLeverageLags, thengjruses their values to determineQinstead.Otherwise,
Qis0.
Data Types: double
Conditional variance model constant, specified as a positive scalar or NaN value.
Data Types: double
GARCH polynomial coefficients, specified as a cell vector of positive scalars or NaN values.
If you specify
GARCHLags, then the following conditions apply.The lengths of
GARCHandGARCHLagsare equal.GARCH{is the coefficient of lagj}GARCHLags(.j)By default,
GARCHis anumel(GARCHLags)-by-1 cell vector ofNaNvalues.
Otherwise, the following conditions apply.
The length of
GARCHisP.GARCH{is the coefficient of lagj}j.By default,
GARCHis aP-by-1 cell vector ofNaNvalues.
The coefficients in GARCH correspond to coefficients in an underlying LagOp lag operator polynomial, and are subject to a near-zero tolerance exclusion test. If you set a coefficient to 1e–12 or below, gjr excludes that coefficient and its corresponding lag in GARCHLags from the model.
Data Types: cell
ARCH polynomial coefficients, specified as a cell vector of positive scalars or NaN values.
If you specify
ARCHLags, then the following conditions apply.The lengths of
ARCHandARCHLagsare equal.ARCH{is the coefficient of lagj}ARCHLags(.j)By default,
ARCHis aQ-by-1 cell vector ofNaNvalues. For more details, see theQproperty.
Otherwise, the following conditions apply.
The length of
ARCHisQ.ARCH{is the coefficient of lagj}j.By default,
ARCHis aQ-by-1 cell vector ofNaNvalues.
The coefficients in ARCH correspond to coefficients in an underlying LagOp lag operator polynomial, and are subject to a near-zero tolerance exclusion test. If you set a coefficient to 1e–12 or below, gjr excludes that coefficient and its corresponding lag in ARCHLags from the model.
Data Types: cell
Leverage polynomial coefficients, specified as a cell vector of numeric scalars or NaN values.
If you specify
LeverageLags, then the following conditions apply.The lengths of
LeverageandLeverageLagsare equal.Leverage{is the coefficient of lagj}LeverageLags(.j)By default,
Leverageis aQ-by-1 cell vector ofNaNvalues. For more details, see theQproperty.
Otherwise, the following conditions apply.
The length of
LeverageisQ.Leverage{is the coefficient of lagj}j.By default,
Leverageis aQ-by-1 cell vector ofNaNvalues.
The coefficients in Leverage correspond to coefficients in an underlying LagOp lag operator polynomial, and are subject to a near-zero tolerance exclusion test. If you set a coefficient to 1e–12 or below, gjr excludes that coefficient and its corresponding lag in LeverageLags from the model.
Data Types: cell
This property is read-only.
The model unconditional variance, specified as a positive scalar.
The unconditional variance is
κ is the conditional variance model constant (Constant).
Data Types: double
Innovation mean model offset, or additive constant, specified as a numeric scalar or NaN value.
Data Types: double
Conditional probability distribution of the innovation process
εt, specified as a string or structure
array. gjr stores the value as a structure array.
| Distribution | String | Structure Array |
|---|---|---|
| Gaussian | "Gaussian" | struct('Name',"Gaussian") |
| Student’s t | "t" | struct('Name',"t",'DoF',DoF) |
The 'DoF' field specifies the t distribution
degrees of freedom parameter.
DoF> 2 orDoF=NaN.DoFis estimable.If you specify
"t",DoFisNaNby default. You can change its value by using dot notation after you create the model. For example,Mdl.Distribution.DoF = 3.If you supply a structure array to specify the Student's t distribution, then you must specify both the
'Name'and the'DoF'fields.
Example: Distribution=struct('Name',"t",'DoF',10)
Model description, specified as a string scalar or character vector. gjr stores the value as a string scalar. The default value describes the parametric form of the model, for example
"GJR(1,1) Conditional Variance Model (Gaussian
Distribution)".
Data Types: string | char
Since R2023a
Response series name, specified as a string scalar or character vector.
gjr stores the value as a string scalar.
Example: "StockReturn"
Data Types: string | char
Note
All
NaN-valued model parameters, which include coefficients and the t-innovation-distribution degrees of freedom (if present), are estimable. When you pass the resultinggjrobject and data toestimate, MATLAB estimates allNaN-valued parameters. During estimation,estimatetreats known parameters as equality constraints, that is,estimateholds any known parameters fixed at their values.Typically, the lags in the ARCH and leverage polynomials are the same, but their equality is not a requirement. Differing polynomials occur when:
Either
ARCH{Q}orLeverage{Q}meets the near-zero exclusion tolerance. In this case, MATLAB excludes the corresponding lag from the polynomial.You specify polynomials of differing lengths by specifying
ARCHLagsorLeverageLags, or by setting theARCHorLeverageproperty.
In either case,
Qis the maximum lag between the two polynomials.
Object Functions
estimate | Fit conditional variance model to data |
filter | Filter disturbances through conditional variance model |
forecast | Forecast conditional variances from conditional variance models |
infer | Infer conditional variances of conditional variance models |
simulate | Monte Carlo simulation of conditional variance models |
summarize | Display estimation results of conditional variance model |
Examples
Create a default gjr model object and specify its parameter values using dot notation.
Create a GJR(0,0) model.
Mdl = gjr
Mdl =
gjr with properties:
Description: "GJR(0,0) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 0
Q: 0
Constant: NaN
GARCH: {}
ARCH: {}
Leverage: {}
Offset: 0
Mdl is a gjr model object. It contains an unknown constant, its offset is 0, and the innovation distribution is 'Gaussian'. The model does not have GARCH, ARCH, or leverage polynomials.
Specify two unknown ARCH and leverage coefficients for lags one and two using dot notation.
Mdl.ARCH = {NaN NaN};
Mdl.Leverage = {NaN NaN};
MdlMdl =
gjr with properties:
Description: "GJR(0,2) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 0
Q: 2
Constant: NaN
GARCH: {}
ARCH: {NaN NaN} at lags [1 2]
Leverage: {NaN NaN} at lags [1 2]
Offset: 0
The Q, ARCH, and Leverage properties update to 2, {NaN NaN}, and {NaN NaN}, respectively. The two ARCH and leverage coefficients are associated with lags 1 and 2.
Create a gjr model object using the shorthand notation gjr(P,Q), where P is the degree of the GARCH polynomial and Q is the degree of the ARCH and leverage polynomials.
Create an GJR(3,2) model.
Mdl = gjr(3,2)
Mdl =
gjr with properties:
Description: "GJR(3,2) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 3
Q: 2
Constant: NaN
GARCH: {NaN NaN NaN} at lags [1 2 3]
ARCH: {NaN NaN} at lags [1 2]
Leverage: {NaN NaN} at lags [1 2]
Offset: 0
Mdl is a gjr model object. All properties of Mdl, except P, Q, and Distribution, are NaN values. By default, the software:
Includes a conditional variance model constant
Excludes a conditional mean model offset (i.e., the offset is
0)Includes all lag terms in the GARCH polynomial up to lags
PIncludes all lag terms in the ARCH and leverage polynomials up to lag
Q
Mdl specifies only the functional form of a GJR model. Because it contains unknown parameter values, you can pass Mdl and time-series data to estimate to estimate the parameters.
Create a gjr model using name-value pair arguments.
Specify a GJR(1,1) model.
Mdl = gjr('GARCHLags',1,'ARCHLags',1,'LeverageLags',1)
Mdl =
gjr with properties:
Description: "GJR(1,1) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
Q: 1
Constant: NaN
GARCH: {NaN} at lag [1]
ARCH: {NaN} at lag [1]
Leverage: {NaN} at lag [1]
Offset: 0
Mdl is a gjr model object. The software sets all parameters to NaN, except P, Q, Distribution, and Offset (which is 0 by default).
Since Mdl contains NaN values, Mdl is only appropriate for estimation only. Pass Mdl and time-series data to estimate.
Create a GJR(1,1) model with mean offset
where
and is an independent and identically distributed standard Gaussian process.
Mdl = gjr('Constant',0.0001,'GARCH',0.35,... 'ARCH',0.1,'Offset',0.5,'Leverage',{0.03 0 0.01})
Mdl =
gjr with properties:
Description: "GJR(1,3) Conditional Variance Model with Offset (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
Q: 3
Constant: 0.0001
GARCH: {0.35} at lag [1]
ARCH: {0.1} at lag [1]
Leverage: {0.03 0.01} at lags [1 3]
Offset: 0.5
gjr assigns default values to any properties you do not specify with name-value pair arguments. An alternative way to specify the leverage component is 'Leverage',{0.03 0.01},'LeverageLags',[1 3].
Access the properties of a gjr model object using dot notation.
Create a gjr model object.
Mdl = gjr(3,2)
Mdl =
gjr with properties:
Description: "GJR(3,2) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 3
Q: 2
Constant: NaN
GARCH: {NaN NaN NaN} at lags [1 2 3]
ARCH: {NaN NaN} at lags [1 2]
Leverage: {NaN NaN} at lags [1 2]
Offset: 0
Remove the second GARCH term from the model. That is, specify that the GARCH coefficient of the second lagged conditional variance is 0.
Mdl.GARCH{2} = 0Mdl =
gjr with properties:
Description: "GJR(3,2) Conditional Variance Model (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 3
Q: 2
Constant: NaN
GARCH: {NaN NaN} at lags [1 3]
ARCH: {NaN NaN} at lags [1 2]
Leverage: {NaN NaN} at lags [1 2]
Offset: 0
The GARCH polynomial has two unknown parameters corresponding to lags 1 and 3.
Display the distribution of the disturbances.
Mdl.Distribution
ans = struct with fields:
Name: "Gaussian"
The disturbances are Gaussian with mean 0 and variance 1.
Specify that the underlying disturbances have a t distribution with five degrees of freedom.
Mdl.Distribution = struct('Name','t','DoF',5)
Mdl =
gjr with properties:
Description: "GJR(3,2) Conditional Variance Model (t Distribution)"
SeriesName: "Y"
Distribution: Name = "t", DoF = 5
P: 3
Q: 2
Constant: NaN
GARCH: {NaN NaN} at lags [1 3]
ARCH: {NaN NaN} at lags [1 2]
Leverage: {NaN NaN} at lags [1 2]
Offset: 0
Specify that the ARCH coefficients are 0.2 for the first lag and 0.1 for the second lag.
Mdl.ARCH = {0.2 0.1}Mdl =
gjr with properties:
Description: "GJR(3,2) Conditional Variance Model (t Distribution)"
SeriesName: "Y"
Distribution: Name = "t", DoF = 5
P: 3
Q: 2
Constant: NaN
GARCH: {NaN NaN} at lags [1 3]
ARCH: {0.2 0.1} at lags [1 2]
Leverage: {NaN NaN} at lags [1 2]
Offset: 0
To estimate the remaining parameters, you can pass Mdl and your data to estimate and use the specified parameters as equality constraints. Or, you can specify the rest of the parameter values, and then simulate or forecast conditional variances from the GARCH model by passing the fully specified model to simulate or forecast, respectively.
Fit a GJR model to an annual time series of stock price index returns from 1861-1970.
Load the Nelson-Plosser data set. Convert the yearly stock price indices (SP) to returns. Plot the returns.
load Data_NelsonPlosser; sp = price2ret(DataTable.SP); figure; plot(dates(2:end),sp); hold on; plot([dates(2) dates(end)],[0 0],'r:'); % Plot y = 0 hold off; title('Returns'); ylabel('Return (%)'); xlabel('Year'); axis tight;

The return series does not seem to have a conditional mean offset, and seems to exhibit volatility clustering. That is, the variability is smaller for earlier years than it is for later years. For this example, assume that an GJR(1,1) model is appropriate for this series.
Create a GJR(1,1) model. The conditional mean offset is zero by default. The software includes a conditional variance model constant by default.
Mdl = gjr('GARCHLags',1,'ARCHLags',1,'LeverageLags',1);
Fit the GJR(1,1) model to the data.
EstMdl = estimate(Mdl,sp);
GJR(1,1) Conditional Variance Model (Gaussian Distribution):
Value StandardError TStatistic PValue
_________ _____________ __________ ________
Constant 0.0045728 0.0044199 1.0346 0.30086
GARCH{1} 0.55808 0.24 2.3253 0.020057
ARCH{1} 0.20461 0.17886 1.144 0.25263
Leverage{1} 0.18066 0.26802 0.67406 0.50027
EstMdl is a fully specified gjr model object. That is, it does not contain NaN values. You can assess the adequacy of the model by generating residuals using infer, and then analyzing them.
To simulate conditional variances or responses, pass EstMdl to simulate.
To forecast innovations, pass EstMdl to forecast.
Simulate conditional variance or response paths from a fully specified gjr model object. That is, simulate from an estimated gjr model or a known gjr model in which you specify all parameter values.
Load the Nelson-Plosser data set. Convert the yearly stock price indices to returns.
load Data_NelsonPlosser;
sp = price2ret(DataTable.SP);Create a GJR(1,1) model. Fit the model to the return series.
Mdl = gjr(1,1); EstMdl = estimate(Mdl,sp);
GJR(1,1) Conditional Variance Model (Gaussian Distribution):
Value StandardError TStatistic PValue
_________ _____________ __________ ________
Constant 0.0045728 0.0044199 1.0346 0.30086
GARCH{1} 0.55808 0.24 2.3253 0.020057
ARCH{1} 0.20461 0.17886 1.144 0.25263
Leverage{1} 0.18066 0.26802 0.67406 0.50027
Simulate 100 paths of conditional variances and responses from the estimated GJR model.
numObs = numel(sp); % Sample size (T) numPaths = 100; % Number of paths to simulate rng(1); % For reproducibility [VSim,YSim] = simulate(EstMdl,numObs,'NumPaths',numPaths);
VSim and YSim are T-by- numPaths matrices. Rows correspond to a sample period, and columns correspond to a simulated path.
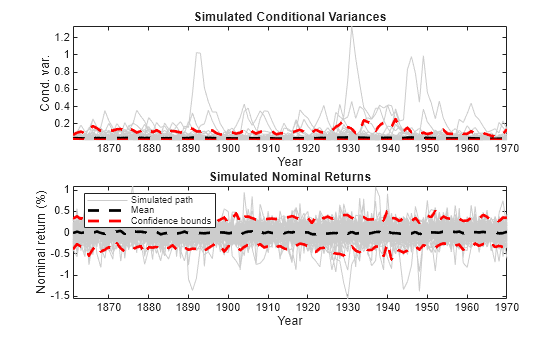
Plot the average and the 97.5% and 2.5% percentiles of the simulated paths. Compare the simulation statistics to the original data.
dates = dates(2:end); VSimBar = mean(VSim,2); VSimCI = quantile(VSim,[0.025 0.975],2); YSimBar = mean(YSim,2); YSimCI = quantile(YSim,[0.025 0.975],2); figure; subplot(2,1,1); h1 = plot(dates,VSim,'Color',0.8*ones(1,3)); hold on; h2 = plot(dates,VSimBar,'k--','LineWidth',2); h3 = plot(dates,VSimCI,'r--','LineWidth',2); hold off; title('Simulated Conditional Variances'); ylabel('Cond. var.'); xlabel('Year'); axis tight; subplot(2,1,2); h1 = plot(dates,YSim,'Color',0.8*ones(1,3)); hold on; h2 = plot(dates,YSimBar,'k--','LineWidth',2); h3 = plot(dates,YSimCI,'r--','LineWidth',2); hold off; title('Simulated Nominal Returns'); ylabel('Nominal return (%)'); xlabel('Year'); axis tight; legend([h1(1) h2 h3(1)],{'Simulated path' 'Mean' 'Confidence bounds'},... 'FontSize',7,'Location','NorthWest');
Forecast conditional variances from a fully specified gjr model object. That is, forecast from an estimated gjr model or a known gjr model in which you specify all parameter values.
Load the Nelson-Plosser data set. Convert the yearly stock price indices (SP) to returns.
load Data_NelsonPlosser;
sp = price2ret(DataTable.SP);Create a GJR(1,1) model and fit it to the return series.
Mdl = gjr('GARCHLags',1,'ARCHLags',1,'LeverageLags',1); EstMdl = estimate(Mdl,sp);
GJR(1,1) Conditional Variance Model (Gaussian Distribution):
Value StandardError TStatistic PValue
_________ _____________ __________ ________
Constant 0.0045728 0.0044199 1.0346 0.30086
GARCH{1} 0.55808 0.24 2.3253 0.020057
ARCH{1} 0.20461 0.17886 1.144 0.25263
Leverage{1} 0.18066 0.26802 0.67406 0.50027
Forecast the conditional variance of the nominal return series 10 years into the future using the estimated GJR model. Specify the entire return series as presample observations. The software infers presample conditional variances using the presample observations and the model.
numPeriods = 10; vF = forecast(EstMdl,numPeriods,sp);
Plot the forecasted conditional variances of the nominal returns. Compare the forecasts to the observed conditional variances.
v = infer(EstMdl,sp); nV = size(v,1); dates = dates((end - nV + 1):end); figure; plot(dates,v,'k:','LineWidth',2); hold on; plot(dates(end):dates(end) + 10,[v(end);vF],'r','LineWidth',2); title('Forecasted Conditional Variances of Returns'); ylabel('Conditional variances'); xlabel('Year'); axis tight; legend({'Estimation Sample Cond. Var.','Forecasted Cond. var.'},... 'Location','NorthWest');

More About
The Glosten, Jagannathan, and Runkle (GJR) model is a dynamic model that addresses conditional heteroscedasticity, or volatility clustering, in an innovations process. Volatility clustering occurs when an innovations process does not exhibit significant autocorrelation, but the variance of the process changes with time.
The GJR model is a generalization of the GARCH model that is appropriate for modeling asymmetric volatility clustering [1]. Specifically, the model posits that the current conditional variance is the sum of these linear processes, with coefficients:
Past conditional variances (the GARCH component or polynomial).
Past squared innovations (the ARCH component or polynomial).
Past squared, negative innovations (the leverage component or polynomial).
Consider the time series
where The GJR(P,Q) conditional variance process, , has the form
The table shows how the variables correspond to the properties of the gjr object. In the table, I[x < 0] = 1, and 0 otherwise.
| Variable | Description | Property |
|---|---|---|
| μ | Innovation mean model constant offset | 'Offset' |
| κ > 0 | Conditional variance model constant | 'Constant' |
| γj | GARCH component coefficients | 'GARCH' |
| αj | ARCH component coefficients | 'ARCH' |
| ξj | Leverage component coefficients | 'Leverage' |
| zt | Series of independent random variables with mean 0 and variance 1 | 'Distribution' |
For stationarity and positivity, GJR models use these constraints:
GJR models are appropriate when negative shocks of contribute more to volatility than positive shocks [2].
If all leverage coefficients are zero, then the GJR model reduces to the GARCH model. Because the GARCH model is nested in the GJR model, you can use likelihood ratio tests to compare a GARCH model fit against a GJR model fit.
Tips
You can specify a gjr model as part of a composition of conditional mean and variance models. For details, see arima.
References
[1] Glosten, L. R., R. Jagannathan, and D. E. Runkle. “On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks.” The Journal of Finance. Vol. 48, No. 5, 1993, pp. 1779–1801.
[2] Tsay, R. S. Analysis of Financial Time Series. 3rd ed. Hoboken, NJ: John Wiley & Sons, Inc., 2010.
Version History
Introduced in R2012aName the response series of a GJR model by setting the
SeriesName property of the associated model to a string
scalar. When you supply input response data to model object functions in a table or
timetable, the functions choose the variable with name SeriesName
as the response variable by default.
Describe a GJR model by setting the Description property to a
string scalar.
The indices of cell arrays of lag operator polynomial coefficients follow MATLAB cell array indexing rules.
Affected model properties are GARCH, ARCH, and
Leverage properties.
You cannot access any lag-zero coefficients by using an index of
0. For example,Mdl.ARCH{0}issues an error.Remove any instances of such indices of zero from your code. The value of all lag-zero coefficients is
1except for the lag operator polynomial corresponding to theARCHproperty, which has the value0.You cannot index beyond the maximal lag in the polynomial. For example, if
Mdl.Pis 4, thenMdl.ARCH{p}issues an error whenpis greater than4. For details on the maximal lags of the lag operator polynomials, see the corresponding property descriptions.Remove any instances of such indices beyond the maximal lag from your code. All coefficients beyond the maximal lag are
0.
The Name field of the Distribution property of
gjr model objects stores the innovation distribution name
as a string scalar, for example, "Gaussian" for Gaussian innovations.
Before R2018a, MATLAB stored the innovation distribution name as a character vector, for example
'Gaussian' for Gaussian innovations. Although most text-data
operations accept character vectors and string scalars for text-data input, the two data
types have some differences. For details, see Text in String and Character Arrays.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)