simulate

Simulate sample paths of Markov-switching dynamic regression model

Syntax

Y = simulate(Mdl,numObs)

Y = simulate(Mdl,numObs,Name,Value)

[Y,E,StatePaths] = simulate(___)

Description

Y = simulate(Mdl,numObs) returns a random numObs-period path of response series Y from simulating the fully specified Markov-switching dynamic regression model Mdl.

Y = simulate(Mdl,numObs,Name,Value) uses additional options specified by one or more name-value arguments. For example, 'NumPaths',1000,'Y0',Y0 simulates 1000 sample paths and initializes the dynamic component of each submodel by using the presample response data Y0.

[Y,E,StatePaths] = simulate(___) also returns the simulated innovation paths E and the simulated state paths StatePaths, using any of the input argument combinations in the previous syntaxes.

Examples

Simulate Response Path

Simulate a response path from a two-state Markov-switching dynamic regression model for a 1-D response process. This example uses arbitrary parameter values.

Create Fully Specified Model

Create a two-state discrete-time Markov chain model that describes the regime switching mechanism. Label the regimes.

P = [0.9 0.1; 0.3 0.7];
mc = dtmc(P,'StateNames',["Expansion" "Recession"]);

mc is a fully specified dtmc object.

For each regime, use arima to create an AR model that describes the response process within the regime. Store the submodels in a vector.

mdl1 = arima('Constant',5,'AR',[0.3 0.2],...
    'Variance',2);
mdl2 = arima('Constant',-5,'AR',0.1,...
    'Variance',1);
mdl = [mdl1; mdl2];

mdl1 and mdl2 are fully specified arima objects.

Create a Markov-switching dynamic regression model from the switching mechanism mc and the vector of submodels mdl.

Mdl = msVAR(mc,mdl);

Mdl is a fully specified msVAR object.

Simulate Response Path

Generate one random response path of length 50 from the model.

rng(1); % For reproducibility
y = simulate(Mdl,50);

y is a 50-by-1 vector of one response path.

Plot the response path.

figure
plot(y)
xlabel("Time")
ylabel("Response")

Simulate Multiple Paths

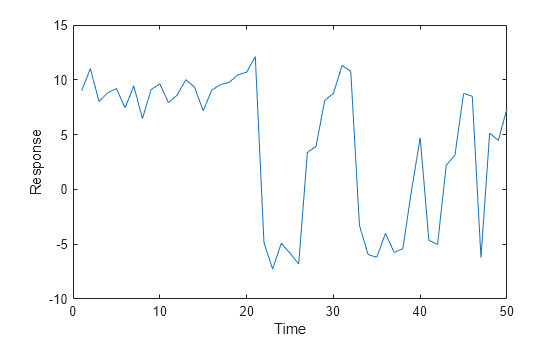
Consider the model in Simulate Response Path.

Create the Markov-switching dynamic regression model.

P = [0.9 0.1; 0.3 0.7];
mc = dtmc(P,'StateNames',["Expansion" "Recession"]);
mdl1 = arima('Constant',5,'AR',[0.3 0.2],...
    'Variance',2);
mdl2 = arima('Constant',-5,'AR',0.1,...
    'Variance',1);
mdl = [mdl1; mdl2];
Mdl = msVAR(mc,mdl);

Simulate 3 response, innovations, and state-index paths of 5 observations from the model.

rng('default') % For reproducibility
[Y,E,SP] = simulate(Mdl,5,'NumPaths',3)

Y = 5×3

   -5.7605   10.9496   11.4633
   -5.7002    8.5772   -3.1268
    4.2446   10.7774   -5.6161
   -3.1665   -2.2920   -5.2677
   -3.8995   -4.7403   -6.3141

E = 5×3

   -0.2050    0.9496    1.4633
   -0.1241   -1.7076    0.7269
    2.1068    1.0143   -0.3034
    1.4090    1.6302    0.2939
    1.4172    0.4889   -0.7873

SP = 5×3

     2     1     1
     2     1     2
     1     1     2
     2     2     2
     2     2     2

Y, E, and SP are 5-by-3 matrices. Columns represent separate, independent paths.

Simulate a single path of responses, innovations, and states into a simulation horizon of length 50. Then plot each path separately.

[y,e,sp] = simulate(Mdl,50);

figure
subplot(3,1,1) 
plot(y)
ylabel('Response')
grid on
subplot(3,1,2)
plot(e)
ylabel('Innovation')
grid on
subplot(3,1,3)
plot(sp,'m')
ylabel('State')
yticks([1 2])
yticklabels(Mdl.StateNames)

Simulate US GDP Rates and Economic States

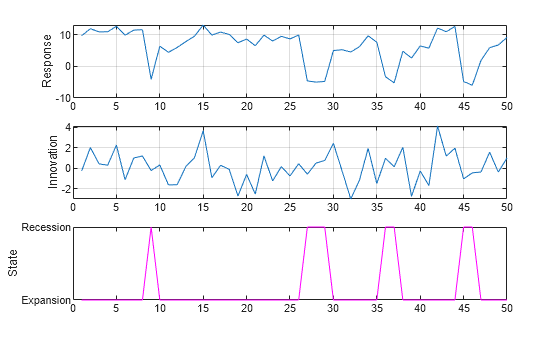
Consider a two-state Markov-switching dynamic regression model of the postwar US real GDP growth rate. The model has the parameter estimates presented in [1].

Create a discrete-time Markov chain model that describes the regime switching mechanism. Label the regimes.

P = [0.92 0.08; 0.26 0.74];
mc = dtmc(P,'StateNames',["Expansion" "Recession"]);

Create separate AR(0) models (constant only) for the two regimes.

sigma = 3.34; % Homoscedastic models across states
mdl1 = arima('Constant',4.62,'Variance',sigma^2);
mdl2 = arima('Constant',-0.48,'Variance',sigma^2);
mdl = [mdl1 mdl2];

Create the Markov-switching dynamic regression model that describes the behavior of the US GDP growth rate.

Mdl = msVAR(mc,mdl);

Mdl is a fully specified msVAR object.

Generate one random path of 100 responses, corresponding innovations, and states from the model.

rng(1) % For reproducibility
[y,e,sp] = simulate(Mdl,100);

y is a 100-by-1 vector of GDP rates, and e is a 100-by-1 vector of corresponding innovations. sp is a 100-by-1 vector of state indices.

Specify Presample Data

Consider the Markov-switching model in Simulate US GDP Rates and Economic States, but assume that the submodels are AR(1) instead. Consider fitting the model to observations in the period 1960:Q1–2004:Q2.

Create the model template for estimation. Specify AR(1) submodels.

mc = dtmc(NaN(2),'StateNames',["Expansion" "Recession"]);
ar1 = arima(1,0,0);
Mdl = msVAR(mc,[ar1; ar1]);

Because the submodels are AR(1), each requires one presample observation to initialize its dynamic component for estimation.

Create the model containing initial parameter values for the estimation procedure.

mc0 = dtmc(0.5*ones(2),'StateNames',["Expansion" "Recession"]);
submdl01 = arima('Constant',1,'Variance',1,'AR',0.001);
submdl02 = arima('Constant',-1,'Variance',1,'AR',0.001);
Mdl0 = msVAR(mc0,[submdl01; submdl02]);

Load the data. Transform the entire set to an annualized rate series.

load Data_GDP
qrate = diff(Data)./Data(1:(end - 1)); 
arate = 100*((1 + qrate).^4 - 1);

Identify the presample and estimation sample periods using the dates associated with the annualized rate series. Because the transformation applies the first difference, you must drop the first observation date from the original sample.

dates = datetime(dates(2:end),'ConvertFrom','datenum',...
    'Format','yyyy:QQQ','Locale','en_US');
estPrd = datetime(["1960:Q2" "2004:Q2"],'InputFormat','yyyy:QQQ',...
    'Format','yyyy:QQQ','Locale','en_US');
idxEst = isbetween(dates,estPrd(1),estPrd(2));
idxPre = dates < estPrd(1);

Fit the model to the estimation sample data. Specify the presample observation.

y0 = arate(idxPre);
EstMdl = estimate(Mdl,Mdl0,arate(idxEst),'Y0',y0);

Simulate a response path from the fitted model over the estimation period. Specify the presample observation.

rng(1) % For reproducibility
numObs = sum(idxEst);
aratesim = simulate(EstMdl,numObs,'Y0',y0);

Plot the observations and simulated path of annualized rates, and identify periods of recession by using recessionplot.

figure;
plot(dates(idxEst),[arate(idxEst) aratesim])
recessionplot
xlabel("Time")
ylabel("Annualized GDP Rate")
legend("Observed","Simulated");

Fit Model to Simulated Data

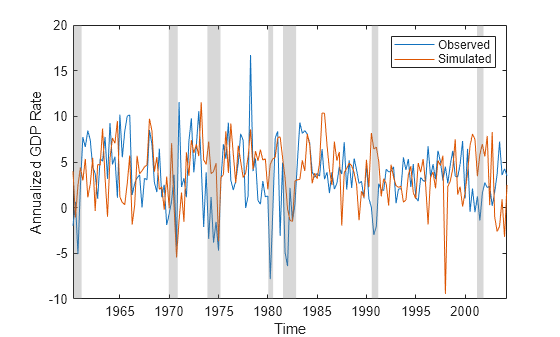
Assess estimation accuracy using simulated data from a known data-generating process (DGP). This example uses arbitrary parameter values.

Create Model for DGP

Create a fully specified, two-state discrete-time Markov chain model for the switching mechanism.

P = [0.7 0.3; 0.1 0.9];
mc = dtmc(P);

For each state, create a fully specified AR(1) model for the response process.

% Constants
C1 = 5;
C2 = -2;

% Autoregression coefficients
AR1 = 0.4;
AR2 = 0.2;

% Variances
V1 = 4;
V2 = 2;

% AR Submodels
dgp1 = arima('Constant',C1,'AR',AR1,'Variance',V1);
dgp2 = arima('Constant',C2,'AR',AR2,'Variance',V2);

Create a fully specified Markov-switching dynamic regression model for the DGP.

DGP = msVAR(mc,[dgp1,dgp2]);

Simulate Response Paths from DGP

Generate 10 random response paths of length 1000 from the DGP.

rng(1); % For reproducibility
N = 10;
n = 1000;
Data = simulate(DGP,n,'Numpaths',N);

Data is a 1000-by-10 matrix of simulated responses.

Create Model for Estimation

Create a partially specified Markov-switching dynamic regression model that has the same structure as the data-generating process, but specify an unknown transition matrix and unknown submodel coefficients.

PEst = NaN(2);
mcEst = dtmc(PEst);
mdl = arima(1,0,0);
Mdl = msVAR(mcEst,[mdl; mdl]);

Create Model Containing Initial Values

Create a fully specified Markov-switching dynamic regression model that has the same structure as Mdl, but set all estimable parameters to initial values.

P0 = 0.5*ones(2);
mc0 = dtmc(P0);
mdl01 = arima('Constant',1,'AR',0.5,'Variance',2);
mdl02 = arima('Constant',-1,'AR',0.5,'Variance',1);
Mdl0 = msVAR(mc0,[mdl01,mdl02]);

Estimate Models

Fit the model to each simulated path. For each path, plot the loglikelihood at each iteration of the EM algorithm.

c1 = zeros(N,1);
c2 = zeros(N,1);
v1 = zeros(N,1);
v2 = zeros(N,1);
ar1 = zeros(N,1);
ar2 = zeros(N,1);
PStack = zeros(2,2,N);

figure
hold on

for i = 1:N

    EstModel = estimate(Mdl,Mdl0,Data(:,i),'IterationPlot',true);
    
    c1(i) = EstModel.Submodels(1).Constant;
    c2(i) = EstModel.Submodels(2).Constant;
    v1(i) = EstModel.Submodels(1).Covariance;
    v2(i) = EstModel.Submodels(2).Covariance;
    ar1(i) = EstModel.Submodels(1).AR{1};
    ar2(i) = EstModel.Submodels(2).AR{1};
    PStack(:,:,i) = EstModel.Switch.P;
    
end

hold off

Assess Accuracy

Compute the Monte Carlo mean of each estimated parameter.

c1Mean = mean(c1);
c2Mean = mean(c2);
v1Mean = mean(v1);
v2Mean = mean(v2);
ar1Mean = mean(ar1);
ar2Mean = mean(ar2);
PMean = mean(PStack,3);

Compare population parameters to the corresponding Monte Carlo estimates.

DGPvsEstimate = [...
    C1  c1Mean
    C2  c2Mean
    V1  v1Mean
    V2  v2Mean
    AR1 ar1Mean
    AR2 ar2Mean]

DGPvsEstimate = 6×2

    5.0000    5.0260
   -2.0000   -1.9615
    4.0000    3.9710
    2.0000    1.9903
    0.4000    0.4061
    0.2000    0.2017

P

P = 2×2

    0.7000    0.3000
    0.1000    0.9000

PEstimate = PMean

PEstimate = 2×2

    0.7065    0.2935
    0.1023    0.8977

Simulate Paths from Model with VARX Submodels

Generate random paths from a three-state Markov-switching dynamic regression model for a 2-D VARX response process. This example uses arbitrary parameter values for the DGP.

Create Fully Specified Model for DGP

Create a three-state discrete-time Markov chain model for the switching mechanism.

P = [10 1 1; 1 10 1; 1 1 10];
mc = dtmc(P);

mc is a fully specified dtmc object. dtmc normalizes the rows of P so that they sum to 1.

For each regime, use varm to create a VAR model that describes the response process within the regime. Specify all parameter values.

% Constants
C1 = [1;-1];
C2 = [2;-2];
C3 = [3;-3];

% Autoregression coefficients
AR1 = {};                            
AR2 = {[0.5 0.1; 0.5 0.5]};          
AR3 = {[0.25 0; 0 0] [0 0; 0.25 0]}; 

% Regression coefficients
Beta1 = [1;-1];           
Beta2 = [2 2;-2 -2];      
Beta3 = [3 3 3;-3 -3 -3]; 

% Innovations covariances
Sigma1 = [1 -0.1; -0.1 1];
Sigma2 = [2 -0.2; -0.2 2];
Sigma3 = [3 -0.3; -0.3 3];

% VARX submodels
mdl1 = varm('Constant',C1,'AR',AR1,'Beta',Beta1,'Covariance',Sigma1);
mdl2 = varm('Constant',C2,'AR',AR2,'Beta',Beta2,'Covariance',Sigma2);
mdl3 = varm('Constant',C3,'AR',AR3,'Beta',Beta3,'Covariance',Sigma3);
mdl = [mdl1; mdl2; mdl3];

mdl contains three fully specified varm model objects.

For the DGP, create a fully specified Markov-switching dynamic regression model from the switching mechanism mc and the submodels mdl.

Mdl = msVAR(mc,mdl);

Mdl is a fully specified msVAR model.

Simulate Data Ignoring Regression Component

If you do not supply exogenous data, simulate ignores the regression components in the submodels. Simulate 3 separate, independent paths of responses, innovations, and state indices of length 5 from the model.

rng(1); % For reproducibility
[Y,E,SP] = simulate(Mdl,5,'NumPaths',3)

Y = 
Y(:,:,1) =

    5.2387    1.5297
    4.4290    4.2738
    1.1668   -1.2905
   -0.9654   -0.2028
   -0.2701    0.8993


Y(:,:,2) =

    2.7737   -2.5383
   -0.8651   -1.1046
   -0.0511    0.3696
    0.5826   -0.8926
    2.4022   -0.6912


Y(:,:,3) =

    3.5443    0.8768
    4.9748   -0.7956
    5.7213    0.8073
    4.2473    0.5805
    2.7972   -1.3340

E = 
E(:,:,1) =

    1.2387    1.5297
   -0.3434    2.8896
    0.1668   -0.2905
   -1.9654    0.7972
   -1.2701    1.8993


E(:,:,2) =

    1.7737   -1.5383
   -1.8651   -0.1046
   -1.0511    1.3696
   -0.4174    0.1074
    1.4022    0.3088


E(:,:,3) =

   -0.4557    0.8768
    1.1150   -1.0061
    1.3134    0.7176
   -0.6941   -0.6838
    1.7972   -0.3340

SP = 5×3

     2     1     2
     2     1     2
     1     1     2
     1     1     2
     1     1     1

Y and E are 5-by-2-by-3 arrays of simulated responses and innovations, respectively. Rows correspond to time points, columns correspond to variables in the system, and pages correspond to paths. SP is a 5-by-3 matrix whose columns correspond to paths.

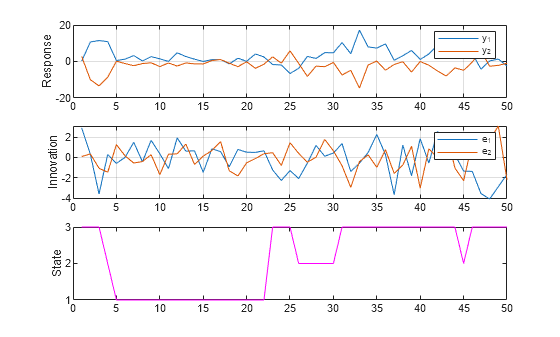
Simulate a single path of responses, innovations, and states into a simulation horizon of length 50. Then plot each path separately.

rng0 = rng; % Store settings to reproduce state sequence.
[Y,E,SP] = simulate(Mdl,50);

figure
subplot(3,1,1)
plot(Y)
ylabel("Response")
grid on
legend(["y_1" "y_2"])
subplot(3,1,2)
plot(E)
ylabel("Innovation")
grid on
legend(["e_1" "e_2"])
subplot(3,1,3)
plot(SP,'m')
ylabel("State")
yticks([1 2 3])

Simulate Data Including Regression Component

Simulate exogenous data for the three regressors by generating 50 random observations from the 3-D standard Gaussian distribution.

X = randn(50,3);

Generate one random response, innovation, and state path of length 50. Specify the simulated exogenous data for the submodel regression components. Plot the results.

rng(rng0); % Reproduce state sequence in previous simulation.
[Y,E,SP] = simulate(Mdl,50,'X',X);

figure
subplot(3,1,1)
plot(Y)
ylabel("Response")
grid on
legend(["y_1" "y_2"])
subplot(3,1,2)
plot(E)
ylabel("Innovation")
grid on
legend(["e_1" "e_2"])
subplot(3,1,3)
plot(SP,'m')
ylabel("State")
yticks([1 2 3])

Perform Monte Carlo Estimation

Consider the model in Simulate Paths from Model with VARX Submodels.

Create Fully Specified Model

Create the Markov-switching model excluding the regression component.

P = [10 1 1; 1 10 1; 1 1 10];
mc = dtmc(P);
C1 = [1;-1];
C2 = [2;-2];
C3 = [3;-3];
AR1 = {};                            
AR2 = {[0.5 0.1; 0.5 0.5]};          
AR3 = {[0.25 0; 0 0] [0 0; 0.25 0]}; 
Sigma1 = [1 -0.1; -0.1 1];
Sigma2 = [2 -0.2; -0.2 2];
Sigma3 = [3 -0.3; -0.3 3];
mdl1 = varm('Constant',C1,'AR',AR1,'Covariance',Sigma1);
mdl2 = varm('Constant',C2,'AR',AR2,'Covariance',Sigma2);
mdl3 = varm('Constant',C3,'AR',AR3,'Covariance',Sigma3);
mdl = [mdl1; mdl2; mdl3];
Mdl = msVAR(mc,mdl);

Simulate Multiple Paths

Generate 1000 random paths of responses for 50 time steps. Start all simulations at the first state.

rng(10); % For reproducibility
S0 = [1 0 0]; 
Y = simulate(Mdl,50,'S0',S0,'NumPaths',1000);

Y is a 50-by-2-by-1000 array of simulated response paths.

Compute Monte Carlo Distribution

For each variable and path, compute the process mean.

mus = mean(Y,1);

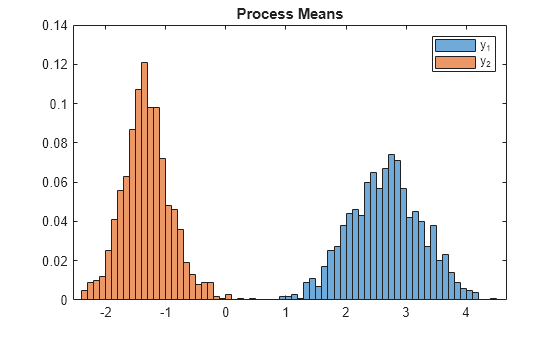
For each variable, plot the Monte Carlo distribution of the process mean.

figure
h1 = histogram(mus(1,1,:),'Normalization',"probability",...
    'BinWidth',0.1);
hold on
h2 = histogram(mus(1,2,:),'Normalization',"probability",...
    'BinWidth',0.1);
legend(["y_1" "y_2"])
title('Process Means')
hold off

For each variable and path, compute the process standard deviation.

sigmas = std(Y,0,1);

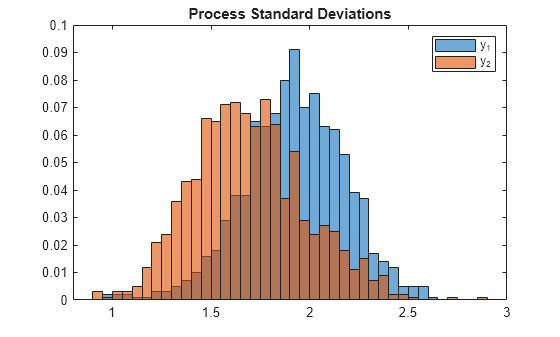
For each variable, plot the Monte Carlo distribution of the process standard deviation.

figure
h1 = histogram(sigmas(1,1,:),'Normalization',"probability",...
    'BinWidth',0.05);
hold on
h2 = histogram(sigmas(1,2,:),'Normalization',"probability",...
    'BinWidth',0.05);
legend(["y_1" "y_2"])
title('Process Standard Deviations')
hold off

Input Arguments

Mdl — Fully specified Markov-switching dynamic regression model

msVAR model object

Fully specified Markov-switching dynamic regression model, specified as an msVAR model object returned by msVAR or estimate. Properties of a fully specified model object do not contain NaN values.

numObs — Number of observations to generate

positive integer

Number of observations to generate for each sample path, specified as a positive integer.

Data Types: double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'NumPaths',1000,'Y0',Y0 simulates 1000 sample paths and initializes the dynamic component of each submodel by using the presample response data Y0.

NumPaths — Number of sample paths to generate

1 (default) | positive integer

Number of sample paths to generate, specified as the comma-separated pair consisting of 'NumPaths' and a positive integer.

Example: 'NumPaths',1000

Data Types: double

Y0 — Presample response data

numeric matrix | numeric array

Presample response data, specified as the comma-separated pair consisting of 'Y0' and a numeric matrix or array.

To use the same presample data for each numPaths path, specify a numPreSampleObs-by-numSeries matrix, where numPaths is the value of NumPaths, numPreSampleObs is the number of presample observations, and numSeries is the number of response variables.

To use different presample data for each path:

• For univariate ARX submodels, specify a numPreSampleObs-by-numPaths matrix.

• For multivariate VARX submodels, specify a numPreSampleObs-by-numSeries-by-numPaths array.

The number of presample observations numPreSampleObs must be sufficient to initialize the AR terms of all submodels. If numPreSampleObs exceeds the AR order of any state, simulate uses the latest observations.

Each time simulate switches states, it updates Y0 using the latest simulated observations.

By default, simulate determines Y0 by the submodel of the initial state (see S0):

• If the initial submodel is a stationary AR process without regression components, simulate sets presample observations to the unconditional mean.

• Otherwise, simulate sets presample observations to zero.

Data Types: double

S0 — Initial state probabilities

nonnegative numeric vector

Initial state probabilities, specified as the comma-separated pair consisting of 'S0' and a nonnegative numeric vector of length numStates.

simulate normalizes S0 to produce a distribution.

simulate selects the initial state of each path from S0 at random. To start from a specific initial state, specify a distribution with a probability mass of 1 in that state.

By default, simulate sets S0 to a steady-state distribution computed by asymptotics.

Example: 'S0',[0.2 0.2 0.6]

Example: 'S0',[0 1] specifies state 2 as the initial state.

Data Types: double

X — Predictor data

numeric matrix | cell vector of numeric matrices

Predictor data used to evaluate regression components in all submodels of Mdl, specified as the comma-separated pair consisting of 'X' and a numeric matrix or a cell vector of numeric matrices.

To use a subset of the same predictors in each state, specify X as a matrix with numPreds columns and at least numObs rows. Columns correspond to distinct predictor variables. Submodels use initial columns of the associated matrix, in order, up to the number of submodel predictors. The number of columns in the Beta property of Mdl.SubModels(j) determines the number of exogenous variables in the regression component of submodel j. If the number of rows exceeds numObs, then simulate uses the latest observations.

To use different predictors in each state, specify a cell vector of such matrices with length numStates.

By default, simulate ignores regression components in Mdl.

Data Types: double

Output Arguments

Y — Simulated response paths

numeric matrix | numeric array

Simulated response paths, returned as a numeric matrix or array. Y represents the continuation of the presample responses in Y0.

For univariate ARX submodels, Y is a numObs-by-numPaths matrix. For multivariate VARX submodels, Y is a numObs-by-numSeries-by-numPaths array.

E — Simulated innovation paths

numeric matrix | numeric array

Simulated innovation paths, returned as a numeric matrix or array.

For univariate ARX submodels, E is a numObs-by-numPaths matrix. For multivariate VARX submodels, E is a numObs-by-numSeries-by-numPaths array.

StatePaths — Simulated state paths

numeric matrix

Simulated state paths, returned as a numObs-by-numPaths numeric matrix.

References

[1] Chauvet, M., and J. D. Hamilton. "Dating Business Cycle Turning Points." In Nonlinear Analysis of Business Cycles (Contributions to Economic Analysis, Volume 276). (C. Milas, P. Rothman, and D. van Dijk, eds.). Amsterdam: Emerald Group Publishing Limited, 2006.

[2] Hamilton, J. D. "Analysis of Time Series Subject to Changes in Regime." Journal of Econometrics. Vol. 45, 1990, pp. 39–70.

[3] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.

Version History

Introduced in R2019b