Test for Cointegration Using the Engle-Granger Test

This example shows how to test the null hypothesis that there are no cointegrating relationships among the response series composing a multivariate model.

Load Data_Canada into the MATLAB® Workspace. The data set contains the term structure of Canadian interest rates [156]. Extract the short-term, medium-term, and long-term interest rate series.

load Data_Canada
Y = Data(:,3:end); % Multivariate response series

Plot the response series.

figure
plot(dates,Y,'LineWidth',2)
xlabel 'Year';
ylabel 'Percent';
names = series(3:end);
legend(names,'location','NW')
title '{\bf Canadian Interest Rates, 1954-1994}';
axis tight
grid on

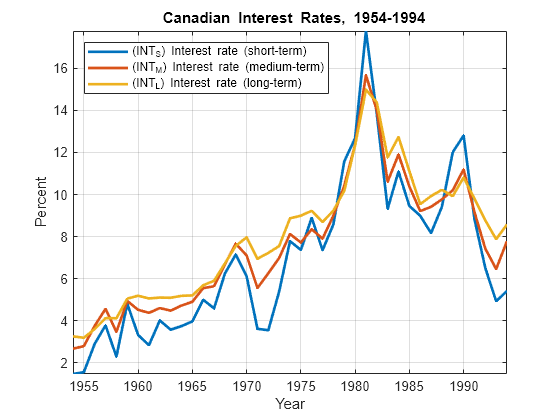
The plot shows evidence of cointegration among the three series, which move together with a mean-reverting spread.

To test for cointegration, compute both the $$\tau$$ (t1) and $$z$$ (t2) Dickey-Fuller statistics. egcitest compares the test statistics to tabulated values of the Engle-Granger critical values.

[h,pValue,stat,cValue] = egcitest(Y,'test',{'t1','t2'})

h = 1x2 logical array

   0   1

pValue = 1×2

    0.0526    0.0202

stat = 1×2

   -3.9321  -25.4538

cValue = 1×2

   -3.9563  -22.1153

The $$\tau$$ test fails to reject the null of no cointegration, but just barely, with a p-value only slightly above the default 5% significance level, and a statistic only slightly above the left-tail critical value. The $$z$$ test does reject the null of no cointegration.

The test regresses Y(:,1) on Y(:,2:end) and (by default) an intercept c0. The residual series is

[Y(:,1) Y(:,2:end)]*beta - c0 = Y(:,1) - Y(:,2:end)*b - c0.

The fifth output argument of egcitest contains, among other regression statistics, the regression coefficients c0 and b.

Examine the regression coefficients to examine the hypothesized cointegrating vector beta = [1; -b].

[~,~,~,~,reg] = egcitest(Y,'test','t2');
 
c0 = reg.coeff(1);
b = reg.coeff(2:3);
beta = [1;-b];
h = gca;
COrd = h.ColorOrder; 
h.NextPlot = 'ReplaceChildren';
h.ColorOrder = circshift(COrd,3); 

plot(dates,Y*beta-c0,'LineWidth',2);
title '{\bf Cointegrating Relation}';
axis tight;
legend off;
grid on;

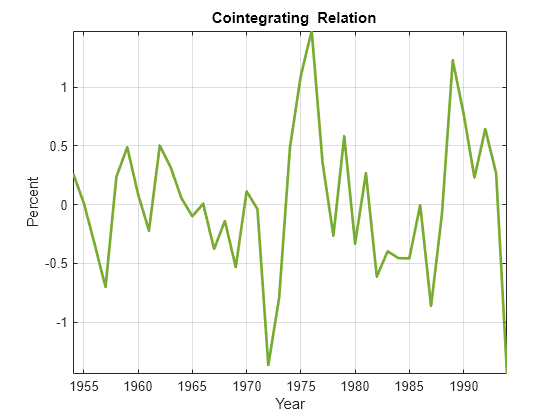
The combination appears relatively stationary, as the test confirms.