interp3

Interpolation for 3-D gridded data in meshgrid format

Syntax

Vq = interp3(X,Y,Z,V,Xq,Yq,Zq)

Vq = interp3(V,Xq,Yq,Zq)

Vq = interp3(V)

Vq = interp3(V,k)

Vq = interp3(___,method)

Vq = interp3(___,method,extrapval)

Description

Vq = interp3(X,Y,Z,V,Xq,Yq,Zq) returns interpolated values of a function of three variables at specific query points using linear interpolation. The results always pass through the original sampling of the function. X, Y, and Z contain the coordinates of the sample points. V contains the corresponding function values at each sample point. Xq, Yq, and Zq contain the coordinates of the query points.

Vq = interp3(V,Xq,Yq,Zq) assumes a default grid of sample points. The default grid points cover the region, X=1:n, Y=1:m, Z=1:p, where [m,n,p] = size(V). Use this syntax when you want to conserve memory and are not concerned about the absolute distances between points.

Vq = interp3(V) returns the interpolated values on a refined grid formed by dividing the interval between sample values once in each dimension.

Vq = interp3(V,k) returns the interpolated values on a refined grid formed by repeatedly halving the intervals k times in each dimension. This results in 2^k-1 interpolated points between sample values.

Vq = interp3(___,method) specifies an alternative interpolation method: 'linear', 'nearest', 'cubic', 'makima', or 'spline'. The default method is 'linear'.

Vq = interp3(___,method,extrapval) also specifies extrapval, a scalar value that is assigned to all queries that lie outside the domain of the sample points.

If you omit the extrapval argument for queries outside the domain of the sample points, then based on the method argument interp3 returns one of the following:

• The extrapolated values for the 'spline' and 'makima' methods

• NaN values for other interpolation methods

Examples

Interpolate Using Default Method

Load the points and values of the flow function, sampled at 10 points in each dimension.

[X,Y,Z,V] = flow(10);

The flow function returns the grid in the arrays, X, Y, Z. The grid covers the region, $$0.1\le X\le 10$$, $$-3\le Y\le 3$$, $$-3\le Z\le 3$$, and the spacing is $$\Delta X=0.5$$, $$\Delta Y=0.7$$, and $$\Delta Z=0.7$$.

Now, plot slices through the volume of the sample at: X=6, X=9, Y=2, and Z=0.

figure
slice(X,Y,Z,V,[6 9],2,0);
shading flat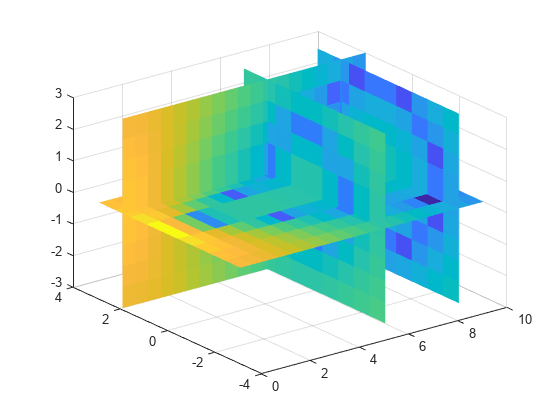

Create a query grid with spacing of 0.25.

[Xq,Yq,Zq] = meshgrid(.1:.25:10,-3:.25:3,-3:.25:3);

Interpolate at the points in the query grid and plot the results using the same slice planes.

Vq = interp3(X,Y,Z,V,Xq,Yq,Zq);
figure
slice(Xq,Yq,Zq,Vq,[6 9],2,0);
shading flat

Interpolate Using Cubic Method

Load the points and values of the flow function, sampled at 10 points in each dimension.

[X,Y,Z,V] = flow(10);

The flow function returns the grid in the arrays, X, Y, Z. The grid covers the region, $$0.1\le X\le 10$$, $$-3\le Y\le 3$$, $$-3\le Z\le 3$$, and the spacing is $$\Delta X=0.5$$, $$\Delta Y=0.7$$, and $$\Delta Z=0.7$$.

Plot slices through the volume of the sample at: X=6, X=9, Y=2, and Z =0.

figure
slice(X,Y,Z,V,[6 9],2,0);
shading flat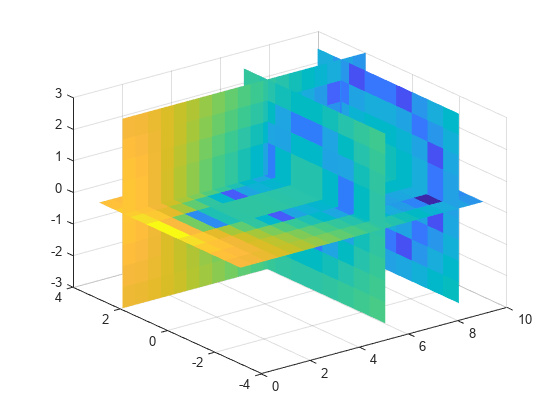

Create a query grid with spacing of 0.25.

[Xq,Yq,Zq] = meshgrid(.1:.25:10,-3:.25:3,-3:.25:3);

Interpolate at the points in the query grid using the 'cubic' interpolation method. Then plot the results.

Vq = interp3(X,Y,Z,V,Xq,Yq,Zq,'cubic');
figure
slice(Xq,Yq,Zq,Vq,[6 9],2,0);
shading flat

Evaluate Outside the Domain of X, Y, and Z

Create the grid vectors, x, y, and z. These vectors define the points associated with values in V.

x = 1:100;
y = (1:50)';
z = 1:30;

Define the sample values to be a 50-by-100-by-30 random number array, V. Use the rand function to create the array.

rng('default')
V = rand(50,100,30);

Evaluate V at three points outside the domain of x, y, and z. Specify extrapval = -1.

xq = [0 0 0];
yq = [0 0 51];
zq = [0 101 102];
vq = interp3(x,y,z,V,xq,yq,zq,'linear',-1)

vq = 1×3

    -1    -1    -1

All three points evaluate to -1 because they are outside the domain of x, y, and z.

Input Arguments

X,Y,Z — Sample grid points

arrays | vectors

Sample grid points, specified as real arrays or vectors. The sample grid points must be unique.

• If X, Y, and Z are arrays, then they contain the coordinates of a full grid (in meshgrid format). Use the meshgrid function to create the X, Y, and Z arrays together. These arrays must be the same size.

• If X, Y, and Z are vectors, then they are treated as a grid vectors. The values in these vectors must be strictly monotonic, either increasing or decreasing.

Example: [X,Y,Z] = meshgrid(1:30,-10:10,1:5)

Data Types: single | double

V — Sample values

array

Sample values, specified as a real or complex array. The size requirements for V depend on the size of X, Y, and Z:

• If X, Y, and Z are arrays representing a full grid (in meshgrid format), then the size of V matches the size of X, Y, or Z .

• If X, Y, and Z are grid vectors, then size(V) = [length(Y) length(X) length(Z)].

If V contains complex numbers, then interp3 interpolates the real and imaginary parts separately.

Example: rand(10,10,10)

Data Types: single | double
Complex Number Support: Yes

Xq,Yq,Zq — Query points

scalars | vectors | arrays

Query points, specified as a real scalars, vectors, or arrays.

• If Xq, Yq, and Zq are scalars, then they are the coordinates of a single query point in R³.

• If Xq, Yq, and Zq are vectors of different orientations, then Xq, Yq, and Zq are treated as grid vectors in R³.

• If Xq, Yq, and Zq are vectors of the same size and orientation, then Xq, Yq, and Zq are treated as scattered points in R³.

• If Xq, Yq, and Zq are arrays of the same size, then they represent either a full grid of query points (in meshgrid format) or scattered points in R³.

Example: [Xq,Yq,Zq] = meshgrid((1:0.1:10),(-5:0.1:0),3:5)

Data Types: single | double

k — Refinement factor

1 (default) | real, nonnegative, integer scalar

Refinement factor, specified as a real, nonnegative, integer scalar. This value specifies the number of times to repeatedly divide the intervals of the refined grid in each dimension. This results in 2^k-1 interpolated points between sample values.

If k is 0, then Vq is the same as V.

interp3(V,1) is the same as interp3(V).

The following illustration depicts k=2 in one plane of R³. There are 72 interpolated values in red and 9 sample values in black.

Example: interp3(V,2)

Data Types: single | double

method — Interpolation method

'linear' (default) | 'nearest' | 'cubic' | 'spline' | 'makima'

Interpolation method, specified as one of the options in this table.

Method	Description	Continuity	Comments
'linear'	The interpolated value at a query point is based on linear interpolation of the values at neighboring grid points in each respective dimension. This is the default interpolation method.	C0	Requires at least two grid points in each dimension Requires more memory than 'nearest'
'nearest'	The interpolated value at a query point is the value at the nearest sample grid point.	Discontinuous	Requires two grid points in each dimension Fastest computation with modest memory requirements
'cubic'	The interpolated value at a query point is based on a cubic interpolation of the values at neighboring grid points in each respective dimension. The interpolation is based on a cubic convolution.	C1	Grid must have uniform spacing in each dimension, but the spacing does not have to be the same for all dimensions Requires at least four points in each dimension Requires more memory and computation time than 'linear'
'makima'	Modified Akima cubic Hermite interpolation. The interpolated value at a query point is based on a piecewise function of polynomials with degree at most three evaluated using the values of neighboring grid points in each respective dimension. The Akima formula is modified to avoid overshoots.	C1	Requires at least 2 points in each dimension Produces fewer undulations than 'spline' Computation time is typically less than 'spline', but the memory requirements are similar
'spline'	The interpolated value at a query point is based on a cubic interpolation of the values at neighboring grid points in each respective dimension. The interpolation is based on a cubic spline using not-a-knot end conditions.	C2	Requires four points in each dimension Requires more memory and computation time than 'cubic'

extrapval — Function value outside domain of X, Y, and Z

scalar

Function value outside domain of X, Y, and Z, specified as a real or complex scalar. interp3 returns this constant value for all points outside the domain of X, Y, and Z.

Example: 5

Example: 5+1i

Data Types: single | double
Complex Number Support: Yes

Output Arguments

Vq — Interpolated values

scalar | vector | array

Interpolated values, returned as a real or complex scalar, vector, or array. The size and shape of Vq depends on the syntax you use and, in some cases, the size and value of the input arguments.

Syntaxes	Special Conditions	Size of Vq	Example
interp3(X,Y,Z,V,Xq,Yq,Zq) interp3(V,Xq,Yq,Zq) and variations of these syntaxes that include method or extrapval	Xq, Yq, and Zq are scalars.	Scalar	size(Vq) = [1 1] when you pass Xq, Yq, and Zq as scalars.
Same as above	Xq, Yq, and Zq are vectors of the same size and orientation.	Vector of same size and orientation as Xq, Yq, and Zq	If size(Xq) = [100 1], and size(Yq) = [100 1], and size(Zq) = [100 1], then size(Vq) = [100 1].
Same as above	Xq, Yq, and Zq are vectors of mixed orientation.	size(Vq) = [length(Y) length(X) length(Z)]	If size(Xq) = [1 100], and size(Yq) = [50 1], and size(Zq) = [1 5], then size(Vq) = [50 100 5].
Same as above	Xq, Yq, and Zq are arrays of the same size.	Array of the same size as Xq, Yq, and Zq	If size(Xq) = [50 25], and size(Yq) = [50 25], and size(Zq) = [50 25], then size(Vq) = [50 25].
interp3(V,k) and variations of this syntax that include method or extrapval	None	Array in which the length of the ith dimension is 2^k * (size(V,i)-1)+1	If size(V) = [10 12 5], and k = 3, then size(Vq) = [73 89 33].

More About

Strictly Monotonic

A set of values that are always increasing or decreasing, without reversals. For example, the sequence, a = [2 4 6 8] is strictly monotonic and increasing. The sequence, b = [2 4 4 6 8] is not strictly monotonic because there is no change in value between b(2) and b(3). The sequence, c = [2 4 6 8 6] contains a reversal between c(4) and c(5), so it is not monotonic at all.

Full Grid (in meshgrid Format)

For interp3, a full grid consists of three arrays whose elements represent a grid of points that define a region in R³. The first array contains the x-coordinates, the second array contains the y-coordinates, and the third array contains the z-coordinates. The values in each array vary along a single dimension and are constant along the other dimensions.

The values in the x-array are strictly monotonic, increasing, and vary along the second dimension. The values in the y-array are strictly monotonic, increasing, and vary along the first dimension. The values in the z-array are strictly monotonic, increasing, and vary along the third dimension. Use the meshgrid function to create a full grid that you can pass to interp3.

Grid Vectors

For interp3, grid vectors consist of three vectors of mixed-orientation that define the points on a grid in R³.

For example, the following code creates the grid vectors for the region, 1 ≤ x ≤ 3, 4 ≤ y ≤ 5, and 6 ≤ z ≤ 8:

x = 1:3;
y = (4:5)';
z = 6:8;

Scattered Points

For interp3, scattered points consist of three arrays or vectors, Xq, Yq, and Zq, that define a collection of points scattered in R³. The ith array contains the coordinates in the ith dimension.

For example, the following code specifies the points, (1, 19, 10), (6, 40, 1), (15, 33, 22), and (0, 61, 13).

Xq = [1 6; 15 0];
Yq = [19 40; 33 61];
Zq = [10 1; 22 13];

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• Xq, Yq, and Zq must be the same size. Use meshgrid to evaluate on a grid.

• For best results, provide X, Y, and Z as vectors. The values in these vectors must be strictly monotonic and increasing.

• Code generation does not support the 'makima' interpolation method.

• For the 'cubic' interpolation method, if the grid does not have uniform spacing, an error results. In this case, use the 'spline' interpolation method.

• For best results when you use the 'spline' interpolation method:

  • Use meshgrid to create the inputs Xq, Yq, and Zq.

  • Use a small number of interpolation points relative to the dimensions of V. Interpolating over a large set of scattered points can be inefficient.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Usage notes and limitations:

• V must be a double or single 3-D array. V can be real or complex.

• X, Y, and Z must:

  • Have the same type (double or single).

  • Be finite vectors or 3-D arrays with increasing and nonrepeating elements in corresponding dimensions.

  • Align with Cartesian axes when X,Y, and Z are 3-D arrays (as if they were produced by meshgrid).

  • Have dimensions consistent with V.

• Xq, Yq, and Zq must be vectors or arrays of the same type (double or single). If Xq, Yq, and Zq are arrays, then they must have the same size. If they are vectors with different lengths, then one of them must have a different orientation.

• method must be 'linear' or'nearest'.

• The extrapolation for the out-of-boundary input is not supported.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays

Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

Version History

Introduced before R2006a