ppval
Evaluate piecewise polynomial
Syntax
Description
Examples
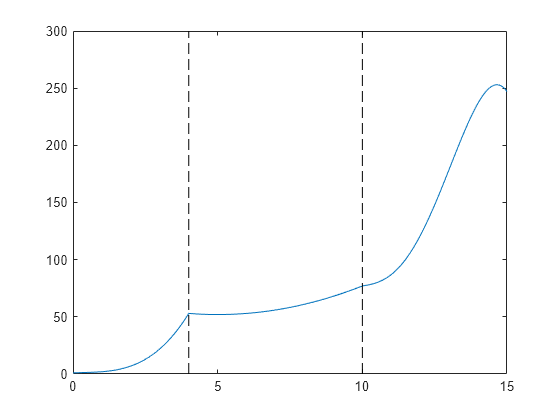
Create a piecewise polynomial that has a cubic polynomial in the interval [0,4], a quadratic polynomial in the interval [4,10], and a quartic polynomial in the interval [10,15].
breaks = [0 4 10 15]; coefs = [0 1 -1 1 1; 0 0 1 -2 53; -1 6 1 4 77]; pp = mkpp(breaks,coefs)
pp = struct with fields:
form: 'pp'
breaks: [0 4 10 15]
coefs: [3×5 double]
pieces: 3
order: 5
dim: 1
Evaluate the piecewise polynomial at many points in the interval [0,15] and plot the results. Plot vertical dashed lines at the break points where the polynomials meet.
xq = 0:0.01:15; plot(xq,ppval(pp,xq)) line([4 4],ylim,'LineStyle','--','Color','k') line([10 10],ylim,'LineStyle','--','Color','k')
Create and plot a piecewise polynomial with four intervals that alternate between two quadratic polynomials.
The first two subplots show a quadratic polynomial and its negation shifted to the intervals [-8,-4] and [-4,0]. The polynomial is
The third subplot shows a piecewise polynomial constructed by alternating these two quadratic pieces over four intervals. Vertical lines are added to show the points where the polynomials meet.
subplot(2,2,1) cc = [-1/4 1 0]; pp1 = mkpp([-8 -4],cc); xx1 = -8:0.1:-4; plot(xx1,ppval(pp1,xx1),'k-') subplot(2,2,2) pp2 = mkpp([-4 0],-cc); xx2 = -4:0.1:0; plot(xx2,ppval(pp2,xx2),'k-') subplot(2,1,2) pp = mkpp([-8 -4 0 4 8],[cc;-cc;cc;-cc]); xx = -8:0.1:8; plot(xx,ppval(pp,xx),'k-') hold on line([-4 -4],ylim,'LineStyle','--') line([0 0],ylim,'LineStyle','--') line([4 4],ylim,'LineStyle','--') hold off

Input Arguments
Output Arguments
Piecewise polynomial values at query points, returned as a vector, matrix, or array.
If pp has [d1,..,dr]-valued
coefficients (nonscalar coefficient values), then:
When
xqis a vector of lengthN,vhas size[d1,...,dr,N], andv(:,...,:,j)is the value atxq(j).When
xqhas size[N1,...,Ns],vhas size[d1,...,dr,N1,...,Ns], andv(:,...,:, j1,...,js)is the value atxq(j1,...,js).
Extended Capabilities
Usage notes and limitations:
The size of output
vdoes not match MATLAB® when both of the following statements are true:The input
xxis a variable-size array that is not a variable-length vector.xxbecomes a row vector at run time.
In this case, the code generator does not remove the singleton dimensions. However, MATLAB might remove singleton dimensions.
For example, suppose that
xxis a :4-by-:5 array (the first dimension is variable size with an upper bound of 4 and the second dimension is variable size with an upper bound of 5). Suppose thatppval(pp,0)returns a 2-by-3 fixed-size array.vhas size 2-by-3-by-:4-by-:5. At run time, suppose that, size(x,1) =1 and size (x,2) = 5. In the generated code, the size(v) is [2,3,1,5]. In MATLAB, the size is [2,3,5].
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
The ppval function
fully supports GPU arrays. To run the function on a GPU, specify the input data as a gpuArray (Parallel Computing Toolbox). For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)