ss2tf
Convert state-space representation to transfer function
Description
Examples
A one-dimensional discrete-time oscillating system consists of a unit mass, , attached to a wall by a spring of unit elastic constant. A sensor samples the acceleration, , of the mass at Hz.
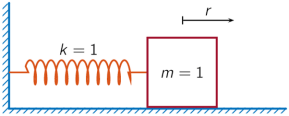
Generate 50 time samples. Define the sampling interval .
Fs = 5; dt = 1/Fs; N = 50; t = dt*(0:N-1);
The oscillator can be described by the state-space equations
where is the state vector, and are respectively the position and velocity of the mass, and the matrices
A = [cos(dt) sin(dt);-sin(dt) cos(dt)]; B = [1-cos(dt);sin(dt)]; C = [-1 0]; D = 1;
The system is excited with a unit impulse in the positive direction. Use the state-space model to compute the time evolution of the system starting from an all-zero initial state.
u = [1 zeros(1,N-1)]; x = [0;0]; for k = 1:N y(k) = C*x + D*u(k); x = A*x + B*u(k); end
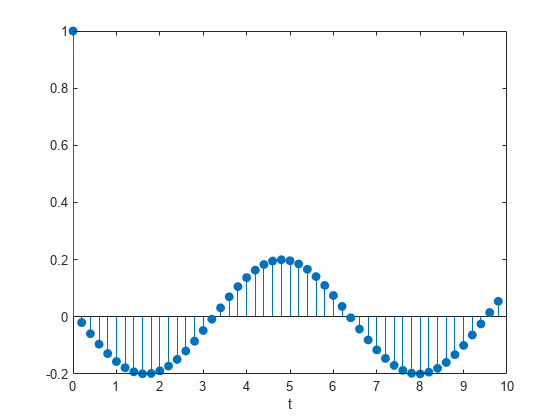
Plot the acceleration of the mass as a function of time.
stem(t,y,'filled') xlabel('t')
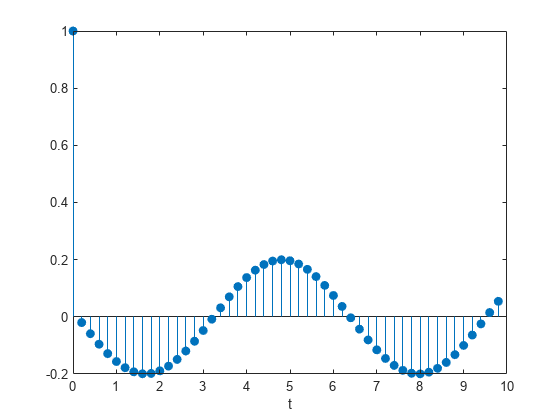
Compute the time-dependent acceleration using the transfer function H(z) to filter the input. Plot the result.
[b,a] = ss2tf(A,B,C,D); yt = filter(b,a,u); stem(t,yt,'filled') xlabel('t')
The transfer function of the system has an analytic expression:
Use the expression to filter the input. Plot the response.
bf = [1 -(1+cos(dt)) cos(dt)]; af = [1 -2*cos(dt) 1]; yf = filter(bf,af,u); stem(t,yf,'filled') xlabel('t')
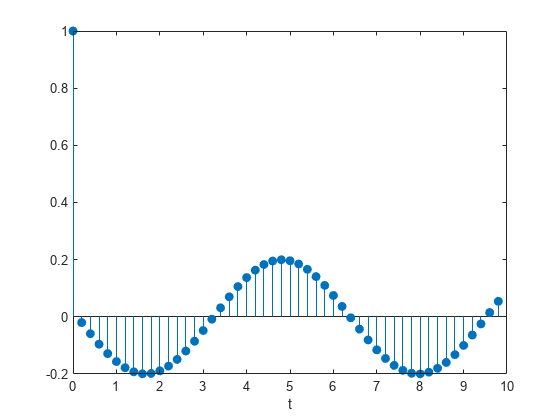
The result is the same in all three cases.
An ideal one-dimensional oscillating system consists of two unit masses, and , confined between two walls. Each mass is attached to the nearest wall by a spring of unit elastic constant. Another such spring connects the two masses. Sensors sample and , the accelerations of the masses, at Hz.
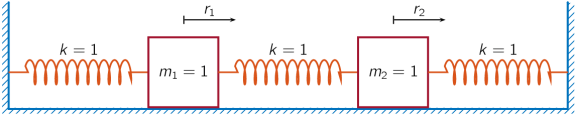
Specify a total measurement time of 16 s. Define the sampling interval .
Fs = 16; dt = 1/Fs; N = 257; t = dt*(0:N-1);
The system can be described by the state-space model
where is the state vector and and are respectively the location and the velocity of the th mass. The input vector and the output vector . The state-space matrices are
the continuous-time state-space matrices are
and denotes an identity matrix of the appropriate size.
Ac = [0 1 0 0; -2 0 1 0; 0 0 0 1; 1 0 -2 0]; A = expm(Ac*dt); Bc = [0 0; 1 0; 0 0; 0 1]; B = Ac\(A-eye(4))*Bc; C = [-2 0 1 0; 1 0 -2 0]; D = eye(2);
The first mass, , receives a unit impulse in the positive direction.
ux = [1 zeros(1,N-1)]; u0 = zeros(1,N); u = [ux;u0];
Use the model to compute the time evolution of the system starting from an all-zero initial state.
x = [0 0 0 0]'; y = zeros(2,N); for k = 1:N y(:,k) = C*x + D*u(:,k); x = A*x + B*u(:,k); end
Plot the accelerations of the two masses as functions of time.
stem(t,y','.') xlabel('t') legend('a_1','a_2') title('Mass 1 Excited') grid
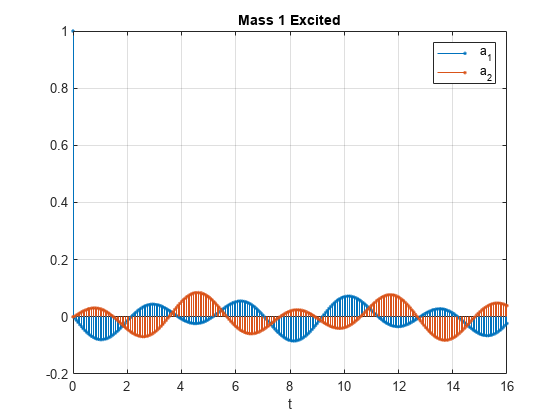
Convert the system to its transfer function representation. Find the response of the system to a positive unit impulse excitation on the first mass.
[b1,a1] = ss2tf(A,B,C,D,1); y1u1 = filter(b1(1,:),a1,ux); y1u2 = filter(b1(2,:),a1,ux);
Plot the result. The transfer function gives the same response as the state-space model.
stem(t,[y1u1;y1u2]','.') xlabel('t') legend('a_1','a_2') title('Mass 1 Excited') grid

The system is reset to its initial configuration. Now the other mass, , receives a unit impulse in the positive direction. Compute the time evolution of the system.
u = [u0;ux]; x = [0;0;0;0]; for k = 1:N y(:,k) = C*x + D*u(:,k); x = A*x + B*u(:,k); end
Plot the accelerations. The responses of the individual masses are switched.
stem(t,y','.') xlabel('t') legend('a_1','a_2') title('Mass 2 Excited') grid
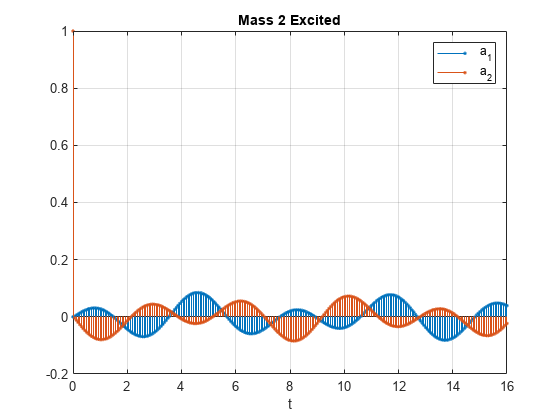
Find the response of the system to a positive unit impulse excitation on the second mass.
[b2,a2] = ss2tf(A,B,C,D,2); y2u1 = filter(b2(1,:),a2,ux); y2u2 = filter(b2(2,:),a2,ux);
Plot the result. The transfer function gives the same response as the state-space model.
stem(t,[y2u1;y2u2]','.') xlabel('t') legend('a_1','a_2') title('Mass 2 Excited') grid
Input Arguments
State matrix, specified as a matrix. If the system has p inputs
and q outputs and is described by n state
variables, then A is n-by-n.
Data Types: single | double
Input-to-state matrix, specified as a matrix. If the system
has p inputs and q outputs and
is described by n state variables, then B is n-by-p.
Data Types: single | double
State-to-output matrix, specified as a matrix. If the system
has p inputs and q outputs and
is described by n state variables, then C is q-by-n.
Data Types: single | double
Feedthrough matrix, specified as a matrix. If the system has p inputs
and q outputs and is described by n state
variables, then D is q-by-p.
Data Types: single | double
Input index, specified as an integer scalar. If the system has p inputs,
use ss2tf with a trailing argument ni = 1, …, p to
compute the response to a unit impulse applied to the nith
input.
Data Types: single | double
Output Arguments
Transfer function numerator coefficients, returned as a vector
or matrix. If the system has p inputs and q outputs
and is described by n state variables, then b is q-by-(n + 1) for each input. The coefficients
are returned in descending powers of s or z.
Transfer function denominator coefficients, returned as a vector.
If the system has p inputs and q outputs
and is described by n state variables, then a is
1-by-(n + 1)
for each input. The coefficients are returned in descending powers
of s or z.
More About
For discrete-time systems, the state-space matrices relate the state vector x, the input u, and the output y through
The transfer function is the Z-transform of the system’s impulse response. It can be expressed in terms of the state-space matrices as
For continuous-time systems, the state-space matrices relate the state vector x, the input u, and the output y through
The transfer function is the Laplace transform of the system’s impulse response. It can be expressed in terms of the state-space matrices as
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)