Solve Differential Equation Using Multigrid Preconditioner on Distributed Discretization
This example shows how to solve Poisson's equation using a preconditioned iterative solver and distributed arrays. By using distributed arrays, you can scale up the calculation using the memory of a cluster of machines, not just the memory of a single machine. You can scale up without changing your code.
This example continues the topics covered in Use Distributed Arrays to Solve Systems of Linear Equations with Iterative Methods. Based on [1], the example models heat distribution in a room by using Poisson's equation, in a form known as the homogeneous steady-state heat equation. Steady state means that the heat does not vary with time and homogeneous means that there is no external heat source.
In the equation, represents the temperature at every point of the room. To solve the equation, you first approximate it by a system of linear equations using a finite difference discretization method. Then, you use the preconditioned conjugate gradients (pcg) method to solve the system. Preconditioning transforms the problem to improve the performance of the numerical solver. By using distributed arrays, you can leverage the combined memory of a cluster of machines and allow finer discretizations.
Learn how to:
Set up a discrete 3-D grid and boundary conditions.
Define a discretization and a multigrid preconditioner.
Apply a preconditioned numerical solver to solve the heat equation across the 3-D volume.
Discretize Spatial Dimensions
In this example, a cube of side 1 models the room. The first step is to discretize it using a 3-D grid.
The preconditioning method in this example uses several grids with different levels of granularity. Each level coarsens the grid by a factor of 2 in each dimension. Define the number of multigrid levels.
multigridLevels = 2;
Define the number of points in each dimension, X, Y, and Z, of the finest grid. The preconditioning method requires that the number of points in this grid be divisible by 2^multigridLevels. In this case, the number of points must be divisible by 4, because the number of multigrid levels is 2.
numPoints.X = 32; numPoints.Y = 32; numPoints.Z = 32;
Discretize the spatial dimensions with a 3-D grid by using the meshgrid function. Divide each dimension uniformly according to the number of points by using linspace. Note that, to include the boundaries of the cube, you must add two additional points.
[X,Y,Z] = meshgrid(linspace(0,1,numPoints.X+2), ... linspace(0,1,numPoints.Y+2), ... linspace(0,1,numPoints.Z+2));
Define Boundary Conditions
Suppose the room has a window and a door. The walls and ceiling have a constant temperature of 0 degrees, the window has a constant temperature of 16 degrees, and the door has a constant temperature of 15 degrees. The floor is at 0.5 degrees. The goal is to determine the temperature distribution across the interior of the room.
Define the coordinates of the floor, window, and door using relational operators, and define the temperature on these boundary elements. The boundaries are the facets of the cube and, therefore, one of X,Y, or Z must be 0 or 1. Set the rest of the boundary and the interior of the cube to 0.
floor = (0.0 <= X & X <= 1.0) & (0.0 <= Y & Y <= 1) & (Z == 0.0); window = (X == 1) & (0.2 <= Y & Y <= 0.8) & (0.4 <= Z & Z <= 0.6); door = (0.4 <= X & X <= 0.6) & (Y == 1.0) & (0.0 <= Z & Z <= 0.6); u = zeros(size(X)); u(floor) = 0.5; u(window) = 16; u(door) = 15;
These boundary conditions specify the constant values that a solution must take along the boundary of the domain. This type of boundary condition is known as the Dirichlet boundary condition.
Visualize the boundary conditions using the slice function. Use slices positioned at the boundary of the cube that show the nonzero boundary conditions.
xSlices = 1; ySlices = 1; zSlices = 0; f = slice(X,Y,Z,u,xSlices,ySlices,zSlices,'nearest'); title('Constant nonzero boundary conditions'), xlabel('x'), ylabel('y'), zlabel('z'); colorbar, colormap cool; shading interp; set(f,'EdgeColor',[0 0 0]);

Discretize and Solve Differential Equation
This example discretizes the differential equation into a linear system using a finite differences approximation method, and uses a multigrid preconditioner to improve the performance of the iterative solver. For this example, use the discretization and the preconditioner in the discretizePoissonEquation and multigridPreconditioner supporting functions. The discretizePoissonEquation function is attached to this example as a supporting file. To access this file, open the example as a live script.
For other problems, choose a discretization and a preconditioner that are appropriate for your application.
In this example, discretizePoissonEquation discretizes Poisson's equation with a seven-point-stencil finite differences method into multiple grids with different levels of granularity. The function creates a multigrid structure of discretizations, with precomputed triangular factorizations and operators that map between coarse and fine levels. The preconditioner uses this multigrid information to approximate the solution in an efficient way.
Among other techniques, this preconditioner applies smoothing to minimize errors with a series of approximations. Define the number of smoothing steps. Using a greater number of steps makes approximations more accurate, but also more computationally intensive. Then, discretize the differential equation and set up the preconditioner.
numberOfSmootherSteps = 1; [A,b,multigridData] = discretizePoissonEquation(numPoints,multigridLevels,numberOfSmootherSteps,u);
Level 0: The problem is of dimension 32768 with 223232 nonzeros. Level 1: The problem is of dimension 4096 with 27136 nonzeros. Level 2: The problem is of dimension 512 with 3200 nonzeros.
preconditioner = setupPreconditioner(multigridData);
Solve the linear system using preconditioned conjugate gradients.
tol = 1e-12; maxit = numel(A); pcg(A,b,tol,maxit,preconditioner);
pcg converged at iteration 45 to a solution with relative residual 5.4e-13.
Scale Up with Distributed Arrays
If you need more computational resources, such as memory, you can scale up using distributed arrays without needing to change your code. Distributed arrays distribute your data across multiple workers and they can leverage the computational performance and memory of a cluster of machines.
Start a pool of parallel workers. By default, parpool uses your default cluster. Check your default cluster profile on the MATLAB Home tab, in the Environment area, in Parallel > Select a Default Cluster.
parpool;
Starting parallel pool (parpool) using the 'MyCluster' profile ... Connected to the parallel pool (number of workers: 12).
Distribute the temperature variable u across the memory of the workers in your cluster by using the distributed function.
distU = distributed(u);
You can use the same code as before; no changes are required because the discretization and preconditioner functions create distributed arrays if the input is a distributed array. Many MATLAB functions are enhanced for distributed arrays, so you can work with them in the same way you work with in-memory arrays.
Note that discretizePoissonEquation returns a structure containing distributed data. To use distributed data inside a structure in a distributed manner, you must create the structure inside an spmd block. You must also call any function that uses it inside an spmd block.
spmd [A,b,multigridData] = discretizePoissonEquation(numPoints,multigridLevels,numberOfSmootherSteps,distU); preconditioner = setupPreconditioner(multigridData); end
Analyzing and transferring files to the workers ...done. Lab 1: Level 0: The problem is of dimension 32768 with 223232 nonzeros. Level 1: The problem is of dimension 4096 with 27136 nonzeros. Level 2: The problem is of dimension 512 with 3200 nonzeros.
Use pcg inside an spmd block to solve the linear system in a distributed manner.
spmd x = pcg(A,b,tol,maxit,preconditioner); end
Lab 1: pcg converged at iteration 45 to a solution with relative residual 5.4e-13.
Plot Results
The solution from the solver is a vector that fits in memory. Send the data from the workers to the client by using gather. Reshape the data back into a 3-D array and reorder the dimensions to produce the final solution. Set the inner part of u to this solution. The outer part, the boundary, already contains the value of the boundary conditions.
x3D = reshape(gather(x),numPoints.X,numPoints.Y,numPoints.Z); u(2:end-1,2:end-1,2:end-1) = permute(x3D, [2, 1, 3]);
Visualize the solution using the slice function. Add additional slices to plot the temperature inside the cube. You can use the Rotate tool, or vary the position of the slices, to explore the solution.
xSlices = [.5,1]; ySlices = [.5,1]; zSlices = [0,.5]; f = slice(X,Y,Z,u,xSlices,ySlices,zSlices,'nearest'); title('Heat distribution'), xlabel('x'), ylabel('y'), zlabel('z'); colorbar, colormap cool; shading interp;
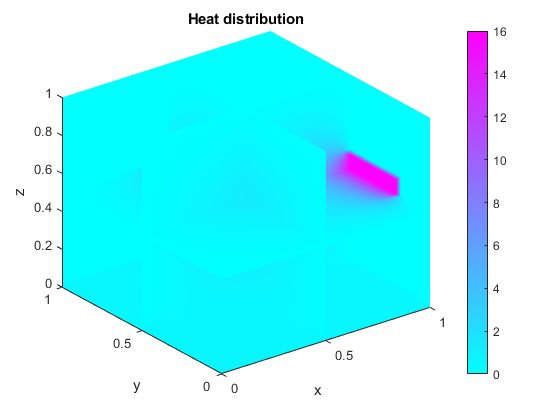
You can try different values of numPoints in this example to test different levels of discretization. Using a larger value increases the resolution, but requires more memory. In addition, the larger multigridLevels is, the more memory efficient the preconditioner is. However, a larger multigridLevels implies a less accurate preconditioner, since coarsening reduces accuracy at every level. As a result, the solver might need more iterations to achieve the same level of accuracy.
Define Preconditioner
Define a multigrid preconditioner for use with the preconditioned conjugate gradients method. This type of preconditioner uses several discretization grids with different levels of granularity to approximate the solution of a system of linear equations more efficiently. The preconditioning method in this example is based on [2], and follows these main stages:
Presmooth using the Gauss-Seidel approximation method.
Compute the residual solution on a coarser level.
Recursively precondition on a coarser level, or solve directly if on the coarsest level.
Update the solution with a coarser grid solution.
Postsmooth using the Gauss-Seidel approximation method.
function x = multigridPreconditioner(mgData,r,level) if(level < mgData(level).MaxLevel) x = zeros(size(r),like=r); % Presmooth using Gauss-Seidel for i=1:mgData(level).NumberOfSmootherSteps x = mgData(level).Matrices.LD \ (-mgData(level).Matrices.U*x + r); x = mgData(level).Matrices.DU \ (-mgData(level).Matrices.L*x + r); end % Compute residual on a coarser level Axf = mgData(level).Matrices.A*x; rc = r(mgData(level).Fine2CoarseOperator)- Axf(mgData(level).Fine2CoarseOperator); % Recursive call until coarsest level is reached xc = multigridPreconditioner(mgData, rc, level+1); % Update solution with prolonged coarse grid solution x(mgData(level).Fine2CoarseOperator) = x(mgData(level).Fine2CoarseOperator)+xc; % Postsmooth using Gauss-Seidel for i = 1:mgData(level).NumberOfSmootherSteps x = mgData(level).Matrices.LD \ (-mgData(level).Matrices.U*x + r); x = mgData(level).Matrices.DU \ (-mgData(level).Matrices.L*x + r); end else % Obtain exact solution on the coarsest level x = mgData(level).Matrices.A \ r; end end
Create a function that takes the multigrid data and returns a function handle that applies the preconditioner to input data. In this example, this function handle is the preconditioner input to pcg. You must create this function because it is not possible to define anonymous functions inside spmd blocks.
function preconditioner = setupPreconditioner(multigridData) if ~isempty(multigridData) preconditioner = @(x,varargin) multigridPreconditioner(multigridData,x,1); else preconditioner = []; end end
References
[1] Dongarra, J., M. A. Heroux, and P. Luszczek. HPCG Benchmark: A New Metric for Ranking High Performance Computing Systems. Knoxville, TN: University of Tennessee, 2015.
[2] Elman, H. C., D. J. Silvester, and A. J. Wathen. Finite Elements and Fast Iterative Solvers: With Applications in Incompressible Fluid Dynamics. Oxford, UK: Oxford University Press, 2005, Section 2.5.
See Also
pcg | distributed | spmd | gather